PROBLEMA Sandro é o dono de uma empresa de segurança que tem como empregados Alberto, Thiago, Robson e Rodrigo. Sandro deve realizar pagamento aos seus empregados totalizando um valor de vinte mil reais. Alberto, Thiago, Robson e Rodrigo recebem pagamentos com valor mínimo de dois mil, dois mil, três mil e quatro mil reais, respectivamente. …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/pagamento-dos-funcionarios/
jul 08
Raiz complicada
PROBLEMA Sem o uso de calculadora, calcule o valor de [tex]\sqrt{4444488889}.[/tex] Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 11, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações para …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/raiz-complicada/
jul 03
Chamada para futuros astronautas!
Dê uma passadinha na nova Sala de Atividades do nosso Blog: Voltando de um passeio pelo mundo da Equação Quadrática – Ideias e aplicações. Nesta sala, vemos como utilizar as equações quadráticas para diversos tipos de problemas: problemas de comprimentos e áreas, problemas de movimento, custo e receita, e questões envolvendo parábolas. Depois disso, …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/chamada-para-futuros-astronautas/
jul 01
Triângulo inscrito
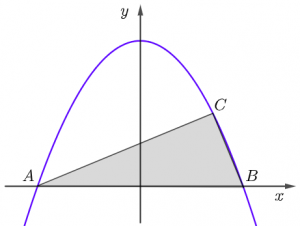
PROBLEMA A curva da figura é dada pela equação [tex]y=-x^2+4[/tex] e o triângulo [tex] ABC[/tex] é retângulo com ângulo reto no vértice [tex]C[/tex]. Calcule a área deste triângulo. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/triangulo-inscrito/
jul 01
Folha dobrada
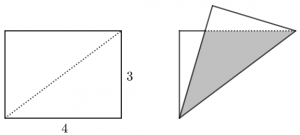
PROBLEMA Uma folha de papel retangular medindo [tex]4[/tex] unidades de comprimento e [tex]3[/tex] unidades de altura foi dobrada ao longo da linha tracejada indicada na figura. Determine a área do triângulo sombreado. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/folha-dobrada/
AVISO
Se você utiliza equipamentos da Apple, por favor, leia esta mensagem.