PROBLEMA Encontre o resto da divisão de [tex]6^{2024}[/tex] por [tex]37[/tex]. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 18, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações para tentarem …
Categoria: *** Problemão
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/resto-da-divisao/
jul 08
Valor do desconto
PROBLEMA O valor presente [tex]V_{p}[/tex] de uma parcela de um financiamento a ser paga daqui a [tex]t[/tex] meses é dada pela fórmula a seguir em que [tex]i[/tex] é o percentual mensal de juros [tex](0\leq i \leq 100)[/tex] e [tex]p[/tex] é o valor da parcela. [tex]V_{p}= \dfrac {p} {\left(1+\dfrac{i}{100}\right)^{t}}[/tex] Imagine que uma mercadoria, de preço [tex]2p[/tex], …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/valor-do-desconto/
jul 08
Pagamento dos funcionários
PROBLEMA Sandro é o dono de uma empresa de segurança que tem como empregados Alberto, Thiago, Robson e Rodrigo. Sandro deve realizar pagamento aos seus empregados totalizando um valor de vinte mil reais. Alberto, Thiago, Robson e Rodrigo recebem pagamentos com valor mínimo de dois mil, dois mil, três mil e quatro mil reais, respectivamente. …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/pagamento-dos-funcionarios/
jul 01
Triângulo inscrito
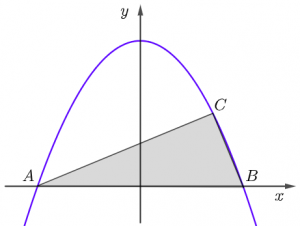
PROBLEMA A curva da figura é dada pela equação [tex]y=-x^2+4[/tex] e o triângulo [tex] ABC[/tex] é retângulo com ângulo reto no vértice [tex]C[/tex]. Calcule a área deste triângulo. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/triangulo-inscrito/
jul 01
Soma dos inversos dos divisores
PROBLEMA Calcule o valor da soma [tex]S=\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{6}+\dfrac{1}{8}+\dfrac{1}{9}+\cdots+ \dfrac{1}{1296},[/tex] em que os denominadores são todos os divisores positivos do número [tex]1296[/tex]. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum. …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/soma-dos-inversos-dos-divisores/