Categoria: Contagem

ago 18

Fila para a fotografia

PROBLEMA Os sete integrantes de um clube de matemática, entre eles dois campeões olímpicos, Noemi e Francimar, vão se posicionar lado a lado para uma fotografia, de maneira que Noemi fique do lado esquerdo de Francimar, não necessariamente juntos. Nessas condições, calcule o número de maneiras diferentes em que esses sete integrantes podem se posicionar …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/08/fila-para-a-fotografia/

jul 07

Pares de conjuntos

PROBLEMA Seja [tex]U=\{a,b,c,d,e\}[/tex] um conjunto com [tex]5[/tex] elementos e sejam [tex]A[/tex] e [tex]B[/tex] subconjuntos de [tex]U[/tex]. Quantos são os pares ordenados [tex](A,B)[/tex] tais que [tex]A\subset B[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 10, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/07/pares-de-conjuntos/

maio 26

Controles

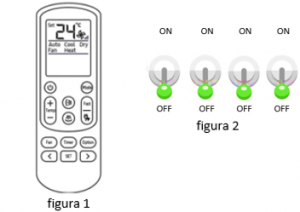
PROBLEMA Uma empresa deseja comprar certa quantidade de aparelhos de ar condicionado para instalação em uma grande sala de reunião, sendo todos do mesmo modelo. Para melhor ajuste da temperatura, cada aparelho de ar condicionado da sala funcionará de maneira independente e terá seu próprio controle remoto (como o da figura 1). A configuração entre …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/controles/

maio 26

Prova do clube

PROBLEMA Para montar uma prova do clube de Matemática, o professor pede aos seus cinco alunos que elaborem três problemas cada. Dois desses problemas serão colocados na prova e dois prêmios iguais serão entregues ao(s) autor(es). De quantas maneiras distintas o professor poderá distribuir os prêmios entre os alunos? Reúnam seus Clubes e tentem resolver …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/prova-do-clube/

maio 12

Crianças na mesa redonda

PROBLEMA Em uma determinada sala de aula, há [tex]8[/tex] meninas e [tex]10[/tex] meninos. Para fazer um trabalho escolar, todos eles devem sentar-se em uma mesa redonda. De quantos modos é possível formar esta mesa redonda sem que haja duas meninas em cadeiras adjacentes? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/criancas-na-mesa-redonda/