PROBLEMA Qual é a maior medida possível para a altura relativa à hipotenusa de um triângulo retângulo, sabendo que essa hipotenusa mede [tex]10[/tex] unidades? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 24, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas …
Categoria: Geometria
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/04/maior-altura/
abr 07
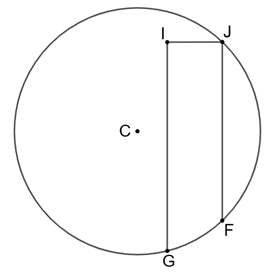
Raio do Círculo
PROBLEMA Na figura abaixo, determine a medida [tex]R[/tex] do raio do círculo de centro [tex]C[/tex], onde [tex]GI=18[/tex], [tex]IJ=6[/tex], [tex]FJ=13[/tex] e os ângulos em [tex]I[/tex] e [tex]J[/tex] são retos. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 10, próxima quinta-feira, visitem a Sala Problemas da Semana: …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/04/raio-do-circulo/
mar 10
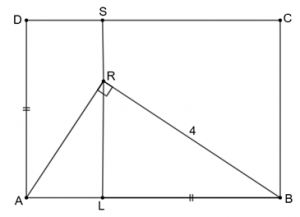
Área do Retângulo
PROBLEMA No interior de um retângulo [tex]ABCD[/tex] constrói-se um triângulo retângulo [tex]ARB[/tex] conforme a figura, no qual o cateto [tex]RB=4[/tex] e [tex]AD\parallel LS[/tex]. Além disso, [tex]\overline{AD}=\overline{LB}[/tex]. Qual é a área do retângulo? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 13, próxima quinta-feira, visitem a …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/03/area-do-retangulo/
mar 10
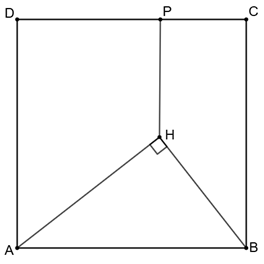
Área do Triângulo Retângulo
PROBLEMA Um quadrado [tex]ABCD[/tex]é dividido em dois trapézios e um triângulo retângulo. As áreas dos trapézios são [tex][ADPH]=9[/tex] e [tex][BCPH]=4[/tex]. Determine a área do triângulo retângulo [tex][ABH][/tex]. Nota: A notação [tex][ABC\dots X][/tex] indica a área do polígono [tex]ABC\dots X[/tex]. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/03/area-do-triangulo-retangulo/
mar 03
Problema: Graveto e triângulo
PROBLEMA Bruno estava brincando com um graveto, quando acertou uma parede e o graveto se partiu em três pedaços, de comprimentos [tex]a,b[/tex] e [tex]c[/tex], com [tex]a \leq b \leq c[/tex]. Ele recolheu os pedaços e tentou construir um triângulo cujos lados seriam exatamente os pedaços do graveto: não foi possível. Sabendo que o graveto tinha …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/03/problema-graveto-e-triangulo/