PROBLEMA Calcule o valor da soma [tex]S=\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{6}+\dfrac{1}{8}+\dfrac{1}{9}+\cdots+ \dfrac{1}{1296},[/tex] em que os denominadores são todos os divisores positivos do número [tex]1296[/tex]. Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum. …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/soma-dos-inversos-dos-divisores/
jun 24
Troca de Cadeiras
PROBLEMA Ao preparar um salão para um evento, Carmem e sua equipe arrumaram, em filas paralelas, as cadeiras alugadas de uma empresa, de forma que uma fila só era formada após a fila anterior já estar completa com [tex]12[/tex] cadeiras. Inicialmente, eles colocaram duas centenas e nove unidades de cadeiras. Em um segundo momento, eles …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/06/troca-de-cadeiras/
jun 24
Quantidade de Ímpares
PROBLEMA Qual a quantidade de números ímpares, compreendidos entre [tex]1\ 000[/tex] e [tex]9\ 999[/tex], cuja soma dos algarismos é [tex]18[/tex] e que possuem três algarismos iguais? Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 27, próxima quinta-feira, deem uma passadinha na Sala Problemas da …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/06/quantidade-de-impares/
jun 24
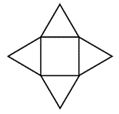
Número Oculto do Quadrado
PROBLEMA Na figura a seguir, cada triângulo e o quadrado central possui um número natural oculto. Em cada uma das situações a seguir, o número que aparece embaixo de cada figura é a soma dos números que estão nos triângulos sombreados e no quadrado central sombreado. Qual o número oculto do quadrado que satisfaz as …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/06/numero-oculto-do-quadrado/
jun 17
Acrescentando algarismos em X
PROBLEMA Seja [tex]X[/tex] o menor número natural com a propriedade de que, ao inserir qualquer algarismo não nulo [tex]c[/tex] após o último algarismo de [tex]X[/tex] (ou seja, à direita de [tex]X[/tex]), o número resultante é sempre divisível por [tex]c[/tex]. Qual é o valor de [tex]X[/tex]? Reúnam seus Clubes e tentem resolver o problema. Mas se …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/06/acrescentando-algarismos-em-x/