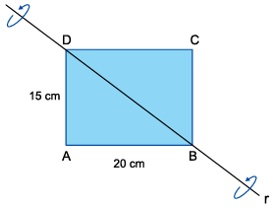
PROBLEMA O retângulo [tex]ABCD[/tex], com [tex]AB=20[/tex] [tex]cm[/tex] e [tex]AD=15[/tex] [tex]cm[/tex], será espacialmente girado de [tex]180^\circ[/tex], tendo como eixo de rotação a reta [tex]r[/tex], que passa por seus vértices [tex]B[/tex] e [tex]D[/tex], como mostra a figura. Calcule o volume do sólido espacial gerado após essa rotação. Reúnam seus Clubes e tentem resolver o problema. Caso não …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/rotacionando-um-retangulo/
nov 15
Sala para leitura: Um pouco sobre Modelagem Matemática
Olá, pessoal! Vocês já ouviram falar em Modelagem Matemática? A Modelagem Matemática é um processo que envolve a representação de situações do mundo real por meio de conceitos matemáticos, com o objetivo de analisar, compreender e prever o comportamento dessas situações. De um lado, têm-se os dados e as intuições fornecidos pelo problema real; …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/sala-para-leitura-um-pouco-sobre-modelagem-matematica/
nov 10
Descobrindo valores para raízes inteiras
PROBLEMA Sabendo que as raízes da equação [tex]x^2-ax+2a=0[/tex] são inteiras, quais são os valores possíveis de [tex]a[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 13, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/descobrindo-valores-para-raizes-inteiras/
nov 10
Descobrir a razão da P. A.
PROBLEMA São inseridos dez números entre os números [tex]2[/tex] e [tex]57[/tex], de modo que esses doze números formem uma progressão aritmética de razão [tex]r[/tex]. Qual o valor de [tex]r[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 13, próxima quinta-feira, visitem a Sala Problemas da …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/descobrir-a-razao-da-p-a/
nov 10
É muita coincidência…
PROBLEMA Qual é a quantidade mínima de pessoas que deve haver em um grupo de modo que possamos garantir que nele haja pelo menos [tex]5[/tex] nascidos no mesmo mês? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 13, próxima quinta-feira, visitem a Sala Problemas da …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/e-muita-coincidencia/