PROBLEMA O termo geral [tex]a_n[/tex] de uma sequência é dado pela fórmula [tex]a_n=3n^2+2[/tex]. Decida se o número [tex]4109[/tex] pertence à sequência e, se sim, determine a sua posição. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 27, próxima quinta-feira, visitem a Sala Problemas da Semana: …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/determine-a-posicao/
nov 24
Uma equação radical
PROBLEMA Encontre as soluções reais da equação [tex]\qquad{\sqrt{1+\sqrt{1+x}}=\sqrt[3]{x}}[/tex]. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 27, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações que ajudam a resolver a questão e …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/uma-equacao-radical/
nov 17
Antivírus
PROBLEMA A probabilidade de um computador estar infectado por um vírus é de [tex]90\%.[/tex] Um programa antivírus detecta a presença de vírus em um computador infectado com probabilidade de [tex]95\%[/tex], mas indica a presença de vírus quando o computador não está infectado com probabilidade de [tex]1\%[/tex]. O programa analisou um dado computador e respondeu que …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/antivirus/
nov 17
Cosseno, cosseno e cosseno
PROBLEMA Calcule o valor do produto [tex]cos\;20^\circ \cdot cos\;40^\circ \cdot cos\;80^\circ[/tex]. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 20, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações que ajudam a resolver …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/cosseno-cosseno-e-cosseno/
nov 17
Rotacionando um retângulo
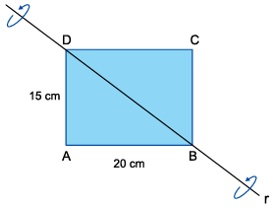
PROBLEMA O retângulo [tex]ABCD[/tex], com [tex]AB=20[/tex] [tex]cm[/tex] e [tex]AD=15[/tex] [tex]cm[/tex], será espacialmente girado de [tex]180^\circ[/tex], tendo como eixo de rotação a reta [tex]r[/tex], que passa por seus vértices [tex]B[/tex] e [tex]D[/tex], como mostra a figura. Calcule o volume do sólido espacial gerado após essa rotação. Reúnam seus Clubes e tentem resolver o problema. Caso não …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/rotacionando-um-retangulo/