PROBLEMA Qual é o maior valor real que [tex]t[/tex] deve assumir na equação [tex](x + 6) (tx -8) (12 + tx) = 0[/tex], de modo que esta só tenha números inteiros como raízes? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 12, próxima quinta-feira, visitem …
Categoria: ** Problema
Problemas Gerais
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/06/procurando-raizes/
jun 02
Expressão Alfabética
PROBLEMA Considere que cada uma das [tex]26[/tex] letras do nosso alfabeto representa um número natural não nulo. Determine o valor da expressão [tex](x-a)\cdot (x-b)\cdot (x-c)\cdot (x-d)\cdot \dots \cdot (x-z).[/tex] Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 5, próxima quinta-feira, visitem a Sala Problemas da …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/06/expressao-alfabetica/
jun 02
Ali Babão Ataca Novamente [tex]4[/tex] – Segunda Temporada
PROBLEMA Resolva a equação [tex]\dfrac{x}{21}+\dfrac{x}{77}+ \dfrac{x}{165}+ \dfrac{x}{285}+ \dfrac{x}{437}+ \dfrac{x}{621}=100.[/tex] Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 5, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações que ajudam a resolver a questão …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/06/ali-babao-ataca-novamente-tex4-tex-segunda-temporada/
maio 26
Prova do clube
PROBLEMA Para montar uma prova do clube de Matemática, o professor pede aos seus cinco alunos que elaborem três problemas cada. Dois desses problemas serão colocados na prova e dois prêmios iguais serão entregues ao(s) autor(es). De quantas maneiras distintas o professor poderá distribuir os prêmios entre os alunos? Reúnam seus Clubes e tentem resolver …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/05/prova-do-clube/
maio 05
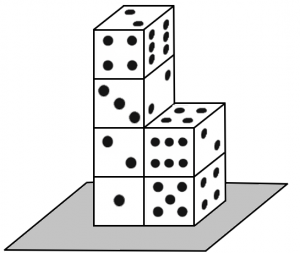
Pilha de dados
PROBLEMA Em um dado comum, faces opostas possuem uma quantidade de sete pontos no total. Observando a configuração abaixo, qual a quantidade mínima de pontos que pode ser visualizada (considerando todos os lados visíveis, sob qualquer ângulo)? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/05/pilha-de-dados/
AVISO
Se você utiliza equipamentos da Apple, por favor, leia esta mensagem.