PROBLEMA Dado que [tex]n!=1\cdot2\cdot3\cdot\dots(n-1) \cdot n[/tex], qual o menor número inteiro positivo [tex]n[/tex] que torna [tex]n![/tex] divisível por [tex]10\ 000[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 4, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá …
Categoria: ** Problema
Problemas Gerais
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/12/texn-tex/
dez 01
[tex](m+p)^2[/tex]
PROBLEMA Se os números [tex]-1[/tex] e [tex]2[/tex] são raízes da equação polinomial [tex]x^3+x^2+mx+p=0[/tex], qual o valor de [tex](m+p)^2[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 4, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/12/texmp2-tex/
nov 10
É muita coincidência…
PROBLEMA Qual é a quantidade mínima de pessoas que deve haver em um grupo de modo que possamos garantir que nele haja pelo menos [tex]5[/tex] nascidos no mesmo mês? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 13, próxima quinta-feira, visitem a Sala Problemas da …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/e-muita-coincidencia/
nov 03
Roleta de Bandeiras
PROBLEMA Com o intuito de incentivar seus alunos, a professora de Geografia de uma escola prometeu presentear o estudante que obtivesse as melhores notas do ano com um atlas. Acontece que cinco alunos empataram na nota final. Sabendo que isso poderia acontecer, a professora preparou uma roleta com [tex]8[/tex] opções de bandeiras de estados brasileiros, …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/roleta-de-bandeiras/
nov 03
Teia de Aranha
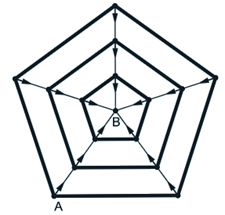
PROBLEMA Uma pesquisadora estuda o deslocamento de uma aranha sobre uma teia artística com formato pentagonal, utilizada em uma instalação de arte urbana. A teia é formada por três anéis pentagonais concêntricos ligados por segmentos radiais (um em cada vértice), como na figura. A aranha parte do vértice A do anel exterior e quer chegar …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/teia-de-aranha/