PROBLEMA Um teste envolvendo o funcionamento da memória de um grupo com muitos indivíduos foi realizado da seguinte forma: foram criados vários cartões contendo em cada um uma imagem e um número associado a ela. Cada uma das pessoas foi exposta a estes cartões por um tempo [tex]t[/tex], em minutos, e em seguida recebeu um …
Categoria: Problemas e Desafios
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/experimento-e-memoria/
out 27
Anagramas
PROBLEMA Quantos anagramas da palavra MORENA podem ser formados de maneira que a letra A sempre aparece antes da letra E e a letra E sempre aparece antes da letra O? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 30, próxima quinta-feira, visitem a Sala …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/anagramas/
out 27
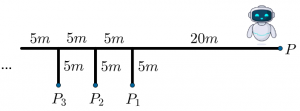
Robô
PROBLEMA O primeiro trajeto de um robô consiste em partir do ponto [tex]P[/tex], ir até o ponto [tex]P_1[/tex] e retornar ao ponto [tex]P[/tex], percorrendo [tex]50\ m[/tex]. No segundo trajeto deve ir do ponto [tex]P[/tex] ao ponto [tex] P_2[/tex] e retornar novamente ao ponto [tex]P[/tex], percorrendo desta vez [tex]60\ m[/tex] e, assim sucessivamente. Sabendo que o …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/robo/
out 20
Arremesso de Dardos
PROBLEMA Os paratletas de Arremesso de Dardos recebem uma letra (A, B, C, D, E ou F) para colocar em destaque em suas camisetas a fim de melhor identificá-los. A representação gráfica abaixo, mostra como analisar a pontuação deles ao final da prova. Usam-se flechas direcionadas para aquele paratleta que possui mais pontos. Por exemplo, …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/arremesso-de-dardos/
out 20
Só log, só log
PROBLEMA Se os números [tex]x_1, x_2, x_3, x_4[/tex] são as soluções da equação [tex]x^4-4x^3-2x^2+12x+9=0[/tex], determine o valor de [tex]log_3{|x_1|}+log_3{|x_2|}+log_3{|x_3|}+log_3{|x_4|}.[/tex] Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 23, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/so-log-so-log/