dez 09
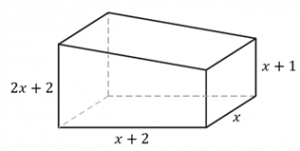
PROBLEMA Um bloco de madeira, com a forma de um prisma reto retangular, foi serrado na parte superior e deu origem ao sólido da figura abaixo Com base nas informações da figura, qual o volume desse sólido? Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2024/12/expressao-para-o-volume/
dez 02
PROBLEMA O estádio do Maracanã passou por algumas modificações estruturais para a realização da Copa do Mundo de 2014, como, por exemplo, as dimensões do campo retangular. Para se adaptar aos padrões da Fifa, as dimensões do campo foram reduzidas de [tex]110 ~m\times 75 ~m[/tex] para [tex]105 ~m\times 68 ~m.[/tex] Em quantos metros quadrados a …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2024/12/reducao-do-maracana/
dez 02
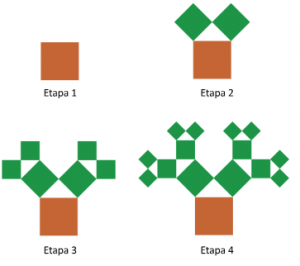
PROBLEMA Uma Árvore Pitagórica é uma figura plana que é construída por etapas. Na Etapa 1, ela começa com um quadrado de lado 1 cm. Na Etapa 2, constroem-se dois quadrados acima do quadrado da Etapa 1, de tal forma que a medida de seus lados seja igual à medida dos catetos do triângulo retângulo …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2024/12/arvore-pitagorica/
nov 25
PROBLEMA Considere um plano [tex]\alpha [/tex] e os pontos [tex]A,B,C[/tex] e [tex]D[/tex] tais que: – o segmento [tex]\overline{AB}[/tex] tem [tex]6[/tex] cm de comprimento e está contido em [tex]\alpha [/tex]; – o segmento [tex]\overline{BC}[/tex] tem [tex]24[/tex] cm de comprimento e está contido em [tex]\alpha [/tex] e é perpendicular a [tex]\overline{AB}[/tex]; – o segmento [tex]\overline{AD}[/tex] tem [tex]8[/tex] …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2024/11/problema-segmentos/
nov 25
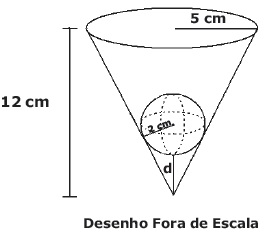
PROBLEMA Uma esfera de [tex]2[/tex] cm de raio é colocada no interior de um vaso cônico, conforme a figura a seguir. O vaso tem [tex]12[/tex] cm de altura e sua abertura é uma circunferência com [tex]5[/tex] cm de raio. Nessas condições, calcule a menor distância ([tex]d[/tex]) entre a esfera e o vértice do cone. Reúnam …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2024/11/problema-distancia-ate-a-esfera/
Se você utiliza equipamentos da Apple, por favor, leia esta mensagem.