Categoria: Aritmética

maio 26

M. D. C e [tex]α[/tex]

PROBLEMA Sabemos que [tex]x=2^{α} \cdot 3 \cdot 7^{4}[/tex], [tex]y=240[/tex] e [tex]z=72[/tex], onde [tex]\alpha[/tex] é um número natural, e que o máximo divisor comum de [tex]x, y[/tex] e [tex]z[/tex] é [tex]12[/tex], qual o valor de [tex]α[/tex]? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 29, próxima …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/m-d-c-e-tex%ce%b1-tex/

maio 18

Jogo dos dígitos

PROBLEMA Considere números de três dígitos formados com os algarismos do conjunto {1, 2, 3, 4}. Uma transformação do tipo A altera o primeiro e o terceiro dígito, substituindo cada um pelo próximo dígito na ordem crescente. Caso o dígito seja 4, ele retorna para 1 (ciclo: 1 → 2 → 3 → 4 → …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/jogo-dos-digitos/

maio 05

Pilha de dados

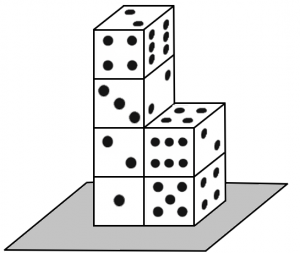
PROBLEMA Em um dado comum, faces opostas possuem uma quantidade de sete pontos no total. Observando a configuração abaixo, qual a quantidade mínima de pontos que pode ser visualizada (considerando todos os lados visíveis, sob qualquer ângulo)? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/05/pilha-de-dados/

abr 28

Racional ou irracional?

PROBLEMA O número [tex] \sqrt{3+2\sqrt{2}} – \sqrt{3-2\sqrt{2}}[/tex] é um número racional ou um número irracional? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 01, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/04/racional-ou-irracional/

abr 21

Sequência limitada

PROBLEMA Considere a sequência [tex](2,9/4, 64/27, \dots) [/tex] com termo geral dado pela fórmula [tex]\qquad{a_n=\left(1+\dfrac{1}{n}\right)^n.}[/tex] Use o fato que [tex]a_n\lt 3[/tex], para todo natural [tex]n[/tex], para decidir qual dos números [tex]99^{100}[/tex] e [tex]100^{99}[/tex] é o maior. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 24, …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/04/sequencia-limitada/