PROBLEMA Qual o quadrado do número [tex]\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}[/tex]? Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 13, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema …
Categoria: Álgebra e números reais
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/02/soma-de-radicais/
fev 03
Quilates
PROBLEMA Muitas joias são constituídas por ligas feitas de uma mistura de ouro puro com outros metais. Uma joia é considerada de ouro [tex]n[/tex] quilates se [tex]\dfrac{n}{24}[/tex] de sua massa for de ouro, sendo [tex]n[/tex] um número inteiro, maior ou igual a [tex]1[/tex] e menor ou igual a [tex]24[/tex]. Uma aliança de ouro [tex]15[/tex] quilates …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2025/02/quilates/
dez 09
Torre em Escala
PROBLEMA A figura a seguir representa duas miniaturas da Torre Eiffel feitas do mesmo material. Sabe-se que a miniatura menor foi feita usando a escala [tex]1:100[/tex] e tem massa de [tex]500[/tex] gramas. Se a segunda torre foi feita na escala [tex]1:50[/tex], qual sua massa? Reúnam seus Clubes e tentem resolver o problema. Mas se não …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/12/torre-em-escala/
dez 09
Problemão: Elevando a [tex]9[/tex]
PROBLEMA Dado [tex]x^2+\dfrac{1}{x^2}=4[/tex], com [tex]x[/tex] um número real positivo, determine o valor de [tex]x^9+\dfrac{1}{x^9}.[/tex] Reúnam seus Clubes e tentem resolver o problema. Mas se não conseguirem, não faz mal. A partir do dia 12, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas. do nosso Fórum. Lá vocês encontrarão Dicas …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/12/problemao-elevando-a-tex9-tex/
dez 02
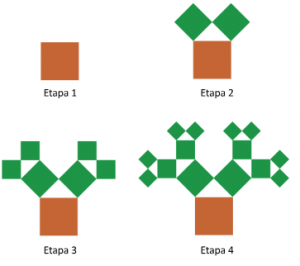
Árvore pitagórica
PROBLEMA Uma Árvore Pitagórica é uma figura plana que é construída por etapas. Na Etapa 1, ela começa com um quadrado de lado 1 cm. Na Etapa 2, constroem-se dois quadrados acima do quadrado da Etapa 1, de tal forma que a medida de seus lados seja igual à medida dos catetos do triângulo retângulo …
Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/12/arvore-pitagorica/