Ali Babão e suas 40 equações
Imagem do menino adaptada de Dreamstime
Ali Babão é um mestre que adora inventar e resolver problemas de matemática.
Ele elaborou uma lista com quarenta problemas envolvendo equações para apresentar aos seus discípulos matemáticos.
Ele elaborou uma lista com quarenta problemas envolvendo equações para apresentar aos seus discípulos matemáticos.
Será que você consegue resolvê-los?
1. Resolva a equação [tex]\boxed{~(x^2-3x+1)^2-3(x^2-3x+1)+1=x~} \, [/tex] no conjunto dos números reais.
Solução
2. Determinar todas as soluções reais da seguinte equação:
[tex]\qquad \qquad \boxed{~\dfrac{x^2}{x-1}+\sqrt{x-1}+\dfrac{\sqrt{x-1}}{x^2}=\dfrac{x-1}{x^2}+\dfrac{1}{\sqrt{x-1}}+\dfrac{x^2}{\sqrt{x-1}}~} \, .[/tex]
Solução
3. Qual a solução da equação [tex]\boxed{4^x+6^x=2\cdot 9^x}[/tex] no conjunto dos números reais?
Solução
4. Resolva a equação [tex] \, \boxed{~\sqrt{3-\sqrt{3+\sqrt{x-\sqrt{2x+1}}}}=1~} \, .[/tex]
Solução
5. Se [tex]\,\boxed{~9^m+9^m+9^m=3^{999}~}\,[/tex], determine [tex]m.[/tex]
Solução
6. Determine todas as soluções reais da equação [tex]\,\boxed{~8x^3-6x-1=0~}\,[/tex].
Solução
7. Vamos brincar com gráficos?
A equação [tex] \boxed{~\left( \dfrac{1}{2} \right) ^x=\left|x-2\right|\;}[/tex] possui solução real?
Solução
8. Sabendo que [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] são números naturais maiores que [tex]1[/tex], resolva a seguinte equação:
[tex]\qquad \qquad \boxed{~a+b+c+a \cdot b+b \cdot c+a \cdot c+a \cdot b \cdot c=2000~}\,[/tex].
Solução
9. Considere a equação [tex]\,\boxed{p^{n}+144=q^{2}}\,[/tex], na qual [tex]n[/tex] e [tex]q[/tex] são números naturais e [tex]p[/tex] é um número primo.
[tex]\qquad[/tex] Encontre os possíveis valores de [tex]n[/tex], [tex] \, q \, [/tex] e [tex] \, p.[/tex]
Solução
10. Resolva a equação [tex]\quad \boxed{~3=\dfrac{1}{1 – \dfrac{1}{1 + \dfrac{1}{1 – \dfrac{1}{x}}}}~} \, [/tex].
Solução
11. Determine todas as soluções reais da equação [tex]\boxed{~(x^2+x+4)^2+8x^3+8x^2+32x+15x^2=0~} \, .[/tex]
Solução
12. Determine todos os pares ordenados de inteiros [tex](x,y)[/tex] tais que [tex]\,\boxed{~9xy-x^{2}-8y^2=2005~}\,[/tex].
Solução
13. Sejam [tex]a[/tex] e [tex]b[/tex] números inteiros. Determinar numericamente as raízes da equação [tex]\,\boxed{~\left(ax-b\right)^2+\left(bx-a\right)^2=x~}\,[/tex], sabendo que essa equação admite uma raiz inteira.
Solução
14. Ali Babão apresentou aos seus discípulos um tipo interessante de equações polinomiais:
- equações cujos coeficientes equidistantes dos extremos ou são todos iguais ou são todos simétricos.
Esquematicamente, são equações da forma
tais que ou
[tex]\qquad \qquad a_n=a_0\,,\, a_{n-1}=a_1\,,\, a_{n-2}=a_2,\cdots\, [/tex]
ou
[tex]\qquad \qquad a_n=-a_0\,,\,a_{n-1}=-a_1\,,\, a_{n-2}=-a_2,\cdots\,. [/tex]
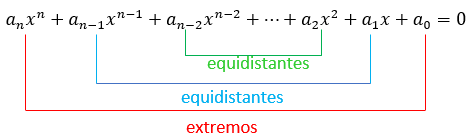
tais que ou
[tex]\qquad \qquad a_n=a_0\,,\, a_{n-1}=a_1\,,\, a_{n-2}=a_2,\cdots\, [/tex]
ou
[tex]\qquad \qquad a_n=-a_0\,,\,a_{n-1}=-a_1\,,\, a_{n-2}=-a_2,\cdots\,. [/tex]
Ajude aos discípulos do mestre Ali, respondendo os itens abaixo.
(a) Se os coeficientes equidistantes dos extremos de uma equação são simétricos, então essa equação admite a raiz [tex]1[/tex]?
(b) Se os coeficientes equidistantes dos extremos de uma equação forem iguais, essa equação admite a raiz [tex]-1[/tex]?
(c) Resolva a equação [tex]\,\boxed{~6x^3-19x^2+19x-6=0~}\,[/tex].
Solução
15. Se [tex]x,\, y[/tex] e [tex]z[/tex] são números reais tais que [tex]x \geqslant 1[/tex], [tex]y \geqslant \frac{1}{2}[/tex] e [tex]z \geqslant \frac{3}{2}\\[/tex], encontre TODAS as soluções da equação
[tex]\qquad \qquad \boxed{~\left(xyz\right)^2=12\left(x-1 \right)\left(2y-1 \right)\left(2z-3 \right)~}\,.[/tex]
Solução
16. Determine todos os valores reais [tex]x, y\, [/tex] e [tex]\, z[/tex] que satisfazem à igualdade [tex]\boxed{~3x^2+y^2+z^2=2xy+2xz~}[/tex].
Solução
17. Resolva a equação [tex]\boxed{~\sqrt[3]{x+9}-\sqrt[3]{x-9}=3~}\,.[/tex]
Solução
18. Encontre todos os reais [tex]x[/tex] para os quais [tex]\,\boxed{~\dfrac{8^x+27^x}{12^x+18^x}=\dfrac{7}{6}~}\,.[/tex]
Solução
19. Quais as raízes reais da equação [tex] \boxed{~\left|\,2x+\sqrt{5}\, \right|=x+4\,\sqrt{5}\,}[/tex]?
Solução
20. Determine os números inteiros [tex]m\,[/tex] e [tex]\,n[/tex] que satisfazem a seguinte equação: [tex]\boxed{\, 2^n+3^m=3^{m+2}-2^{n+1}\, }[/tex].
Solução
21. Se [tex]p[/tex] é um número primo, determinar todas as possíveis soluções inteiras [tex]m[/tex] e [tex]n[/tex] da equação [tex]\; \boxed{~ p \cdot (m+n)=m \cdot n~}\,[/tex].
Solução
22. Quantas soluções com quatro inteiros ímpares tem a equação
[tex]\qquad \qquad \boxed{~\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}=1~}\;[/tex]?
Solução
23. Fixados [tex]m,\,n,\,p,\,q\,[/tex] e [tex]\,r[/tex], determine um valor de [tex]x[/tex] que satisfaça a equação
[tex]\,\\
\qquad \qquad \boxed{~\dfrac{x-m}{n+p+q+r}+\dfrac{x-n-p}{q+r+m}+ \dfrac{x-q-r}{m+n+p}=3~}\,.[/tex]
Solução
24. Quantos pares ordenados [tex] (x,y)[/tex], com [tex]x[/tex] e [tex]y[/tex] números reais, satisfazem a equação [tex]\,\boxed{\,x^2+y^2=|x|+|y|\,}\,[/tex]?
E se [tex]x[/tex] e [tex]y[/tex] forem inteiros?
Solução
25. Para que valores reais [tex]x[/tex] e [tex]y[/tex] a igualdade [tex]\boxed{~5x^{2}+5y^{2}+8xy+2y-2x+2=0~}\,[/tex] é verdadeira?
Solução
26. Resolva no conjunto [tex]\mathbb{R}[/tex] dos números reais a equação [tex]\,\boxed{~x^{2}+4x\,cos(xy)+4=0~}\,.[/tex]
Solução
27. Encontre as soluções reais da equação [tex]\,\boxed{~\sqrt{x+\sqrt{4x-4}}+\sqrt{x-\sqrt{4x-4}}=\sqrt{x+3}~}\,.[/tex]
Solução
28. Quantos pares ordenados [tex](x,y)[/tex] de números reais existem tais que
[tex]\qquad \qquad \boxed{~(2x+3y-1)^4+x^2+y^2=2xy~}\,[/tex]?
Solução
29. Sabendo que [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] são números reais positivos tais que [tex]a \lt b+c[/tex], [tex]b \lt a+c[/tex] e [tex]c \lt a+b[/tex], resolva o sistema abaixo no conjunto dos números reais positivos.
\sqrt{xy}+\sqrt{xz}-x=a\\
\sqrt{yz}+\sqrt{yx}-y=b\\
\sqrt{zx}+\sqrt{zy}-z=c \\
\end{cases}~~[/tex].
Solução
30. Determine a soma e o produto das raízes reais da equação:
Solução
31. Sejam [tex]x[/tex] e [tex]y[/tex] reais positivos tais que [tex]x ^ 3 + y ^ 3 + (x + y) ^ 3 + 30xy = 2000[/tex].
Resolva a equação
[tex]\qquad \qquad \boxed{~ 4x^{4}-ax^{3}+bx^{2}-cx+5=0~},[/tex]
sabendo que todas as raízes [tex]x_{1}, x_{2}, x_{3} [/tex] e [tex] x_{4}[/tex] são reais e positivas e que:
[tex]\qquad \qquad \dfrac{x_{1}}{2}+\dfrac{x_{2}}{4}+\dfrac{x_{3}}{5}+\dfrac{x_{4}}{8}=1.[/tex]
Solução
32. Sejam [tex]x[/tex] e [tex]y[/tex] reais positivos tais que [tex]\boxed{~x ^ 3 + y ^ 3 + (x + y) ^ 3 + 30xy = 2000~}.[/tex]
Mostre que [tex] x + y = 10 [/tex].
Solução
33. Encontre as raízes da equação [tex]\boxed{~(x^{2}-3x-2)^2-3(x^{2}-3x-2)-2-x=0~}.[/tex]
Solução
34. Encontre uma raiz da equação [tex]\boxed{~ x^{x^{20}}=\sqrt[\sqrt{2}]{2}~}.[/tex]
Solução
35.Resolva no conjunto dos números reais a equação [tex]\boxed{~4^x+6^x=9^x~}.[/tex]
Solução
36. Resolva a equação [tex]\boxed{~1+\sqrt{3^{x}}=2^{x}~}.[/tex]
Solução
37. Ali Babão organizou uma gincana na qual deveriam ser resolvidas algumas equações de sua escolha. Robério, um de seus discípulos, recebeu uma ficha com o seguinte problema:
Calcular a soma [tex]S[/tex] das soluções reais da equação [tex]2^x-2^{-x}=5(1-2^{-x}).[/tex]
Robério resolveu corretamente o problema em [tex]2^S[/tex] minutos, sendo que o tempo limite para receber o prêmio da gincana era de [tex]5[/tex] minutos. Robério recebeu o prêmio?
Solução
38.Ali Babão desafiou seu irmão caçula, Ali Babinho, a resolver, no conjunto dos números reais, a equação
Qual é o valor de [tex]B[/tex] ?
Solução
39. Quantos números inteiros satisfazem a equação [tex]\boxed{~2^x \cdot (4-x)=2x+4~}\,[/tex]?
Solução
40. Ache a soma das raízes positivas da equação [tex]\boxed{~4^{x^2}-5\cdot 2^{x^2}+4=0~}.[/tex]
Solução
Equipe COM – OBMEP
F i m d a s a g a !