.Problema para ajudar na escola: Ali Babão e a décima nona de suas 40 equações

Problema
(A partir do 1º ano do E. M.- Nível de dificuldade: Fácil)

(ONEM, 2005) Quais as raízes reais da equação [tex] \boxed{\left|\,2x+\sqrt{5}\, \right|=x+4\,\sqrt{5}\,}[/tex]?

Solução 1

Antes de mais nada, lembre-se de que o valor absoluto de um número real é não negativo; assim, se [tex]x[/tex] for uma raiz da equação em questão, então
[tex]\qquad x+4\sqrt{5} \geqslant 0.\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Aplicando a definição de valor absoluto ao número real [tex]\,2x+\sqrt{5}[/tex], temos duas condições para analisar. Observe.

• Caso 1: [tex]\,2x+\sqrt{5}\geqslant 0[/tex]

Neste caso, pela definição de valor absoluto, [tex]\,\left|\,2x+\sqrt{5}\, \right|=2x+\sqrt{5}\,[/tex] e, portanto, segue que:
[tex]\qquad \left|\,2x+\sqrt{5}\, \right|=x+4\,\sqrt{5}[/tex]
[tex]\qquad 2x+\sqrt{5}=x+4\,\sqrt{5}[/tex]
[tex]\qquad x=3\,\sqrt{5}.[/tex]
Para que esse valor seja solução da equação dada, ele deve satisfazer a condição [tex]\textcolor{#800000}{(i)}[/tex]; vejamos.
[tex]\qquad x+4\sqrt{5}=3\,\sqrt{5}+4\sqrt{5}=7\,\sqrt{5}\gt 0[/tex],
logo, [tex]\boxed{3\,\sqrt{5}}[/tex] é, de fato, raiz da equação do problema.

• Caso 2: [tex]\,2x+\sqrt{5}\lt 0[/tex]

Agora, pela definição de valor absoluto, [tex]\,\left|\,2x+\sqrt{5}\, \right|=-\left(2x+\sqrt{5}\right)\,[/tex] e, assim, segue que:
[tex]\qquad \left|\,2x+\sqrt{5}\, \right|=x+4\,\sqrt{5}[/tex]
[tex]\qquad -\left(2x+\sqrt{5}\right)=x+4\,\sqrt{5}[/tex]
[tex]\qquad -2x-\sqrt{5}=x+4\,\sqrt{5}[/tex]
[tex]\qquad 3x=-5\,\sqrt{5}[/tex]
[tex]\qquad x=-\dfrac{5\,\sqrt{5}}{3}.[/tex]
Mais uma vez, vamos verificar se o valor obtido satisfaz a condição [tex]\textcolor{#800000}{(i)}[/tex].
Como
[tex]\qquad x+4\sqrt{5}=-\dfrac{5\,\sqrt{5}}{3}+4\sqrt{5}=\dfrac{7\,\sqrt{5}}{3}\gt 0[/tex],
então [tex]\boxed{-\dfrac{5\,\sqrt{5}}{3}}[/tex] é mais uma raiz da equação dada.

Portanto, a equação modular [tex] \left|\,2x+\sqrt{5}\, \right|=x+4\,\sqrt{5}\,[/tex] tem duas raízes: [tex]\, \fcolorbox{black}{#eee0e5}{$x_1=3\,\sqrt{5}$}\;[/tex] e [tex]\; \fcolorbox{black}{#eee0e5}{$x_2=-\dfrac{5\,\sqrt{5}}{3}$}\,.[/tex]

Solução elaborada pelos Moderadores do Blog.

Visualização da solução

Vamos fazer uma solução gráfica do problema, traçando o gráfico das funções [tex]f[/tex] e [tex]g[/tex], assim definidas:

[tex]\begin{array}{ccc}
f:\mathbb{R}\rightarrow \mathbb{R}&\qquad \qquad &g:\mathbb{R}\rightarrow \mathbb{R}\\
\boxed{f(x)= \left|\,2x+\sqrt{5}\, \right|}&\qquad \qquad &\boxed{g(x)=x+4\,\sqrt{5}}
\end{array}[/tex]

Aplicando a definição de valor absoluto à expressão que define [tex]f[/tex], podemos reescrever essa função como:
[tex]\qquad f:\mathbb{R}\rightarrow \mathbb{R}\\
\qquad f(x)= \begin{cases}
2x+\sqrt{5},\text{ para } x\geqslant -\dfrac{\sqrt{5}}{2}\\
-2x-\sqrt{5},\text{ para } x\lt -\dfrac{\sqrt{5}}{2}
\end{cases}[/tex].
Para traçar o gráfico de [tex]f[/tex], vamos considerar os gráficos das retas [tex]y=2x+\sqrt{5}[/tex] e [tex]y=-2x-\sqrt{5}[/tex] nos intervalos [tex]\left[-\dfrac{\sqrt{5}}{2},+\infty\right[[/tex] e [tex]\left]-\infty,-\dfrac{\sqrt{5}}{2}\right[[/tex], respectivamente:

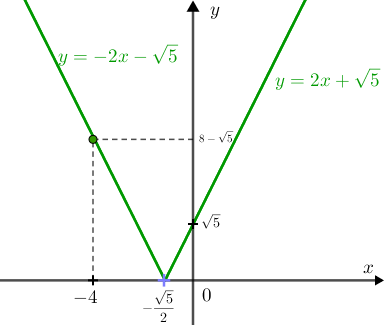
Por outro lado, o gráfico da função [tex]g[/tex] é a reta [tex]y=x+4\,\sqrt{5}\,.[/tex]

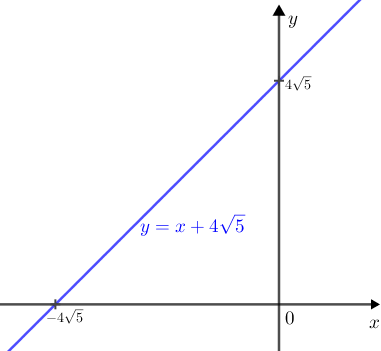
Traçando os dois gráficos em um mesmo plano cartesiano [tex]xOy[/tex], podemos visualizar as duas soluções da equação: são as abscissas dos pontos de interseção dos gráficos das funções [tex]f[/tex] e [tex]g[/tex].

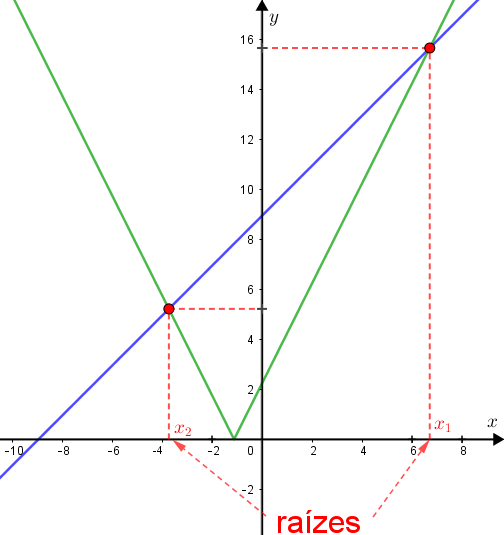
Observe que as raízes da equação são: [tex]\, \fcolorbox{red}{#eee0e5}{$\textcolor{red}{x_1=3\,\sqrt{5}\approx 6,7}$}\;[/tex] e [tex]\; \fcolorbox{red}{#eee0e5}{$\textcolor{red}{x_2=-\dfrac{5\,\sqrt{5}}{3}\approx -3,7}$}\,.[/tex]

Solução elaborada pelos Moderadores do Blog.