Problema
(Indicado a partir do 1º ano do E. M.)
Determine todas as soluções reais da equação [tex]8x^3-6x-1=0[/tex].
Solução
Para resolver este problema, vamos fazer a substituição [tex]\boxed{x=cos\, \alpha}[/tex], transformando a equação dada em [tex]\boxed{8\cdot cos^3\alpha-6\cdot cos\alpha-1=0}\,.[/tex]
Mas para isso, será necessário verificar se as possíveis soluções da equação em questão podem ser valores de cossenos, ou seja, se os possíveis valores reais [tex]x[/tex] tais que [tex]8x^3-6x-1=0[/tex] satisfazem a condição [tex]-1 \leqslant x \leqslant 1.[/tex]
Se você não sabe como justificar essa afirmação, clique no botão abaixo. Caso contrário, siga com a leitura da solução.
Partindo do fato de que
- se existe [tex]x[/tex] real para o qual [tex]8x^3-6x-1=0[/tex], então [tex]-1\le x\le1[/tex],
podemos fazer a substituição [tex]x=cos \,\alpha[/tex], transformando a equação
[tex]\qquad \qquad 8x^3-6x-1=0 \qquad \textcolor{#800000}{(i)}[/tex]
em
[tex]\qquad \qquad 8\cdot cos^3\alpha-6\cdot cos\,\alpha-1=0\,.\qquad \textcolor{#800000}{(ii)}[/tex]
Segue de [tex]\textcolor{#800000}{(ii)}[/tex] que:
[tex]\quad 8\cdot cos^3\alpha-6\cdot cos\,\alpha=1[/tex]
[tex]\quad 2\cdot(4\cdot cos^3\alpha-3\cdot \, cos\alpha)=1[/tex]
[tex]\quad 4\cdot cos^3\alpha-3\cdot cos\, \alpha=\dfrac{1}{2}.\qquad \textcolor{#800000}{(iii)}[/tex]
Utilizando a identidade trigonométrica [tex]\boxed{cos\, 3\alpha =4\cdot cos^3\alpha-3\cdot cos \,\alpha} [/tex], concluímos de [tex]\textcolor{#800000}{(iii)}[/tex] que [tex]\boxed{cos \, 3\alpha=\dfrac{1}{2}}[/tex] e, portanto,
[tex]\quad 3\alpha=60^\circ+360^\circ\cdot k\quad [/tex] ou [tex]\quad 3\alpha=300^\circ+360^\circ\cdot k,\, (k\in \mathbb{Z}) [/tex]
ou, ainda,
[tex]\quad \alpha=20^\circ+120^\circ\cdot k\quad [/tex] ou [tex]\quad \alpha=100^\circ+120^\circ\cdot k\,\, (k\in \mathbb{Z}).[/tex]
Sendo [tex]k \in\mathbb{Z}[/tex], temos infinitos valores para [tex]\alpha[/tex]. Veja alguns deles na tabela a seguir:
[tex]\begin{array}{|c|c|c|}
\hline
\ k & \alpha=20^\circ+120^\circ\cdot k & \alpha=100^\circ+120^\circ\cdot k \\ \hline
-3 & -340^\circ & -260^\circ \\ \hline
-2 & -220^\circ & -140^\circ \\ \hline
-1 & -100^\circ & -20^\circ \\ \hline
0 & 20^\circ & 100^\circ \\ \hline
1 & 140^\circ & 220^\circ \\ \hline
2 & 260^\circ & 340^\circ \\ \hline
3 & 380^\circ & 460^\circ \\ \hline
\end{array}[/tex]
No entanto, como [tex]cos \, \theta=cos(-\theta)[/tex], [tex]cos \, \theta=cos(360^\circ-\theta)[/tex] e [tex]cos \, \theta=cos(360^\circ+\theta)[/tex], ficamos apenas com três soluções para a equação [tex]\textcolor{#800000}{(i)}[/tex]:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x_1=cos 20^\circ$} \quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_2=cos 100^\circ$}\quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_3=cos 140^\circ$}.[/tex]
Em radianos:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x_1=cos\dfrac{\pi}{9}$}\quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_2=cos\dfrac{5\pi}{9}$}\quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_3=cos\dfrac{7\pi}{9}$}.[/tex]
Utilizando uma calculadora ou consultando uma tabela trigonométrica, obtemos as seguintes aproximações para as três soluções da equação [tex]\textcolor{#800000}{(i)}[/tex]:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x_1\approx 0,94$}\quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_2\approx -0,17$}\quad [/tex] ; [tex]\quad \fcolorbox{black}{#eee0e5}{$x_3 \approx -0,77$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Um gráfico para ajudar
Com o auxílio de algum software, podemos visualizar o gráfico da função [tex]f[/tex], de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex], dada por [tex]f(x)=8x^3-6x-1[/tex].
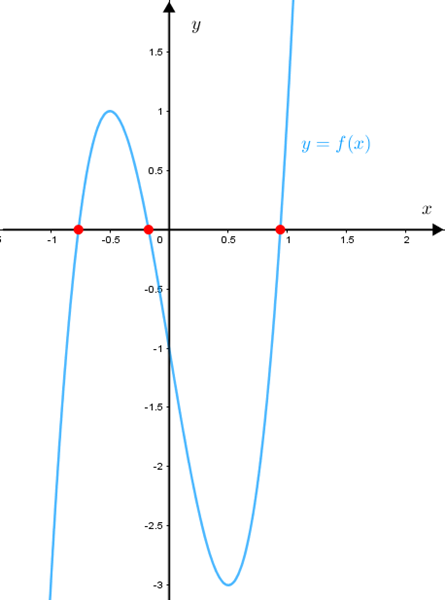
Note que o gráfico de [tex]f[/tex] intercepta o eixo horizontal nos três pontos que estão assinalados em vermelho.
Isso significa que temos três raízes de [tex]f[/tex] ([tex]f(x)=0[/tex]) e, consequentemente, três soluções reais da equação [tex]8x^3-6x-1=0[/tex]:
- uma entre [tex]\boxed{-1}[/tex] e [tex]\boxed{-0,5}[/tex];
- outra entre [tex]\boxed{-0,5}[/tex] e [tex]\boxed{0}[/tex];
- e mais uma entre [tex]\boxed{0,5}[/tex] e [tex]\boxed{1}[/tex].

