PROBLEMA
O poliedro convexo da imagem abaixo é chamado de rombicosidodecaedro.
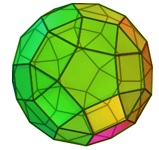
Esse sólido é formado por 62 faces, todas polígonos regulares. Cada vértice desse poliedro é um vértice em comum de dois quadrados, um triângulo e um pentágono.
Qual o número de faces triangulares, quadradas e pentagonais do rombicosidodecaedro?

Mas se não conseguirem, não faz mal. A partir do dia 5, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


8 comentários
Pular para o formulário de comentário
Questão top demais! Acho superdivertido que, apesar da relação de Euler para poliedros convexos ser simples, ela consegue despertar a criatividade nesse tipo de questão.
Relação de Euler para poliedros convexos:
[tex]F+V=A+2[/tex]
Na questão, já temos o valor de [tex]F=62[/tex].
Como diz a questão, cada vértice está ligado a exatamente um triângulo, de modo que cada face triangular contém 3 vértices únicos do poliedro (ou seja, triângulos distintos não compartilham vértices).
Assim, sendo [tex]F_t[/tex] a quantidade de faces triangulares do poliedro, podemos expressar o número total de vértices da figura espacial como:
[tex]V=3F_t[/tex]
Analogamente às faces pentagonais:
[tex]V=5F_p[/tex]
Para as faces quadradas é um pouco diferente, pois cada vértice está associado a duas delas. Desse modo, ao contarmos todas as faces quadradas, estaremos repetindo cada vértice do poliedro exatamente uma vez:
[tex]V=\dfrac{4F_q}{2}=2F_q[/tex]
Essas notações serão importantes para a resposta final. Agora, se atente no seguinte:
Cada vértice faz parte de 4 faces, desse modo, de cada vértice partem 4 arestas.
Porém, cada aresta é sempre ligada por dois vértices (fato que não é exclusivo da questão). Assim, se somarmos as arestas que partem de cada vértice, estaremos repetindo cada aresta exatamente uma vez. Desse modo:
[tex]A=\dfrac{4V}{2}=2V[/tex]
Aplicando no Teorema de Euler:
[tex]62+V=2V+2[/tex]
[tex]V=60[/tex]
Assim, podemos calcular a quantidade de faces triangulares, quadradas e pentagonais:
[tex]3F_t=60\therefore F_t=20[/tex]
[tex]5F_p=60\therefore F_p=12[/tex]
[tex]2F_q=60\therefore F_q=30[/tex]
Autor
Solução correta, Koreil Guys!
Parabéns.
Pela relação de Euler:
V+F=A+2
Já temos que F+62.
Como a questão cita que cada vértice está ligado a exatamente um triângulo, de modo que cada face triangular contém 3 vértices únicos do poliedro (ou seja, triângulos diferentes não dividem o mesmo vértice).
Tendo Ft como o numero de faces triangulares, Fp como o numero de faces pentagonais e Fq como o numero de faces quadradas:
Triangulares:
V= 3Ft
Pentagonais:
V=5Fp
Para as faces quadradas possuem uma particularidade, pois cada vértice está interligado a duas delas. então quando formos contar todas as faces quadradas, estaremos repetindo cada vértice do poliedro exatamente uma vez:
Quadradas:
V= 4Fq/2
V=2Fq
Cada vértice faz parte de 4 faces, desse modo, de cada vértice partem 4 arestas.
No entanto , cada aresta é sempre ligada por dois vértices. Assim, se somarmos as arestas que partem de cada vértice, repetiremos cada aresta uma vez. Então:
A=4V/2
A=2V
Aplicando no Teorema de Euler:
62+V=2V+2
V=60
Agora podemos calcular a quantidade de faces triangulares, quadradas e pentagonais:
5Fp=60 Fp=60/5 Fp=12
2Fq=60 Fq=60/2 Fq=30
3Ft=60 Ft=60/3 Ft=20
Autor
Solução correta, Obmépicos.
Parabéns!
Seja ( v, e, f, p, q, t ) representarem o número total de vértices, arestas, faces, pentágonos, quadriláteros e triângulos no poliedro, respectivamente.
Sabemos que ( v – e + f = 2 ) devido à característica de Euler da superfície.
Também sabemos que ( f = p + q + t ).
Além disso, ( e = (5p + 4q + 3t) / 2 ), pois cada pentágono contribui com cinco arestas, cada quadrilátero contribui com quatro arestas, etc. A divisão por dois vem do fato de que cada aresta é adjacente a duas faces simultaneamente.
Em seguida, ( v = (5p + 4q + 3t) / 4 ), pois, novamente, cada pentágono contribui com cinco vértices, etc., mas cada vértice é adjacente a um total de quatro faces.
Então, juntando essas informações, temos: [ 2 = =v−e+f=[(5p+4q+3t)/4]−[(5p+4q+3t)/2]+p+q+t
Combinando as expressões, temos: [ 8 = 5p + 4q + 3t – 10p – 8q – 6t + 4p + 4q + 4t = t – p ]
Portanto, sabemos que deve haver oito triângulos a mais do que pentágonos.
Para chegar a uma conclusão final sobre o número específico de cada tipo de face, olhamos para como cada forma interage:
Vemos que, do ponto de vista dos pentágonos, há cinco triângulos vizinhos. Então, ( 5p ) contaria em excesso o número de triângulos. Cada triângulo, no entanto, é contado por três pentágonos. Assim, temos a relação ( 5p = 3t ).
Da mesma forma, temos ( 5p = 2q ).
Combinando isso com a informação que tínhamos antes, que ( t = p + 8 ), temos ( 5p = 3(p + 8) ) e, portanto, ( 2p = 24 ) e ( p = 12 ).
Então, ( t = 20 ) e ( q = 30 ).
Devem haver então 20 triângulos, 30 quadriláteros e 12 pentágonos, totalizando ( p + q + t = 62 ) faces.
Também poderíamos voltar e encontrar o número total de vértices e arestas agora que encontramos o número de cada tipo de face.
Autor
Solução correta, LAPLACES.
Parabéns!
O poliedro tem 62 faces. Sabemos que cada aresta é a interseção de duas faces e que cada vértice é formado pela interseção de dois quadrados, um triângulo e um pentágono. Usando a fórmula de Euler para poliedros (V + F = A + 2, com V, F e A sendo o número de vértices, faces e arestas, respectivamente) e considerando P, Q e T como o número de pentágonos, quadrados e triângulos, respectivamente, temos que:
V + F = A + 2
(5P + 4Q + 3T)/4 + 62 = (5P + 4Q + 3T)/2 + 2
5P + 4Q + 3T = 240
Sendo assim, o poliedro possui 240/4 = 60 vértices. Considerando a quantidade de faces em cada vértice (um pentágono, dois quadrados e um triângulo) e a repetição das faces em mais de um vértice (os pentágonos 5 vezes, os quadrados 4 vezes e os triângulos 3 vezes), temos:
P=60/5, Q=120/4 e T=60/3
P=12, Q= 30 e T=20
Autor
Parabéns, Apótema Mineira.
Solução correta!