PROBLEMA
Abaixo temos um quadrado [tex]ABCD[/tex] de lado [tex]4[/tex] cm e centro [tex]X[/tex]. Sabe-se que [tex]AE = BF = 1[/tex] cm.
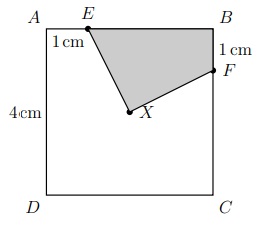
Qual a área do quadrilátero [tex]XEBF[/tex]?
Reúnam seus Clubes e tentem resolver o problema.
Mas se não conseguirem, não faz mal. A partir do dia 3, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Mas se não conseguirem, não faz mal. A partir do dia 3, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!
8 comentários
Pular para o formulário de comentário
Por simetria é possível perceber que o quadrado ABCD pode ser dividido em 4 quadriláteros congruentes a XEBF sempre que AE=BF. Desse modo, a área de XEBF seria [tex]\dfrac{1}{4}(ABCD)=\dfrac{16}{4}=4[/tex]
Outro maneira de pensar é calcular a soma das áreas dos triângulos XEB e XFB:
[tex](XEBF)=(XEB)+(XFB)[/tex]
[tex](XEB)=\dfrac{3\cdot2}{2}=3[/tex]
[tex](XFB)=\dfrac{1\cdot2}{2}=1[/tex]
[tex](XEBF)=3+1=4[/tex]
Autor
As duas soluções estão corretas, Koreil Guys.
Parabéns!!!
Outra maneira de resolver a questão é:
Ao observar o quadrado, podemos perceber que a área do quadrilátero XBEF é uma parte menor que a metade da área do quadrado. Além disso, recortando apenas essa visão da metade, nota-se que além do quadrilátero XBEF, há o trapézio AEXG (G ponto médio de AD) e o triângulo retângulo FXH (H ponto médio de BC), nesse caso podemos calcular a área de XBEF ao descontar as aréas do trapézio e triangulo, em relação à metade da área do quadrado ABDC, então:
At = 4.4 = 16 cm²/2 = 8 cm²
Atrápezio = ((2+1) . 2) / 2 = 3 cm²
Atriangulo = (2 . 1) / 2 = 1 cm²
Assim:
Axbef = At – (Atrapezio + Atriangulo)=
Axbef = 8 – 4 = 4 cm²
Logo, a área do quadriláteo XBEF é 4 cm². Esta resolução é um pouco mais longa, entretanto trabalha com conceitos como área de trapezio e triangulo rentagular.
Autor
Muito bem, Sociedade de Hilbert.
Outra solução correta.
Para resolver esse problema, utilizei um retângulo imaginário formado pela parte de cima do quadrado, traçando uma reta paralela a AB e criando os pontos P, Q, R na mesma coordenada X de A, E e B respectivamente.
Área abrp = 2 . 4 = 8 cm³
Agora subtraí as áreas das figuras brancas restantes:
Área xfr = \frac{2.1}{2} = 1
Área exq = \frac{2.1}{2} = 1
Área aeqp = 2 . 1 = 2
Área abfx = 8 – 1 – 1 – 2 = 4 cm³
Autor
Boa solução, Lógicos.
Estão corretos.
Dividindo XEBF em 2 triângulos congruentes e um retângulo, temos que, a partir das divisões de 1cm e do centro que divide todos os segmentos perpendiculares na metade, temos 2 triângulos de área 1cm² e 1 retângulo de área 2cm²
1cm²+1cm²+2cm² = 4cm²
Autor
Parabéns, Mathlete.
Solução correta!