PROBLEMA
A altura [tex]A(t)[/tex], em quilômetros, do cogumelo de fumaça de uma explosão atômica é uma função do tempo [tex]t[/tex] após a explosão, em minutos. Essa função é dada pela fórmula:
$$A(t)=C \ \text{log} (1+t).$$
Nessa fórmula, [tex]C[/tex] é uma constante que depende da energia da bomba.
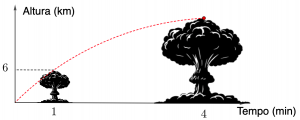
Sabendo-se que, [tex]1[/tex] minuto após a explosão de uma bomba de [tex]1[/tex] megaton de energia, o cogumelo de fumaça tem altura de [tex]6[/tex] km, determine a altura do cogumelo de fumaça desta bomba [tex]3[/tex] minutos após a explosão.

Mas se não conseguirem, não faz mal. A partir do dia 24, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
Primeiramente, temos, se [tex]A(t) = C \cdot \log(1+t)[/tex], e [tex]A(1) = 6[/tex], temos:
$$
6 = C \cdot \log(1 + 1) \Rightarrow 6 = C \cdot \log 2 \therefore C = \frac{6}{\log 2}
$$
Com isso, podemos calcular [tex]A(3)[/tex] da seguinte maneira:
$$
A(3) = C \cdot \log(1 + 3) \Rightarrow A(3) = (\frac{6}{\log 2}) \cdot \log 4 \Rightarrow A(3) = 6 \cdot \frac{\log 4}{\log 2}
$$
Por propriedade de logaritmos, temos [tex]\frac{\log_{c}{a}}{\log_{c}{b}} = \log_{b}{a}[/tex]. Como a base dos logaritmos não está explicita, então estamos lidando com logaritmos de base decimal ([tex]\log_{10}[/tex]), ou seja, podemos reescrever a expressão da seguinte maneira:
$$
A(3) = 6 \cdot \frac{\log 4}{\log 2} \Rightarrow A(3) = 6 \cdot \log_{2}{4}
$$
Como [tex]\log_{2}{4} = 2[/tex], podemos concluir que:
$$
A(3) = 6 \cdot 2 \therefore A(3) = 12
$$
Com isso, concluímos que, [tex]3[/tex] minutos após a explosão de uma bomba com [tex]1[/tex] megaton de energia, o cogumelo de fumaça terá uma altura de [tex]12 \ km[/tex] :D
Autor
A solução está correta Potências de Euler. Parabéns!