PROBLEMA
“O origami é a arte de dobrar papel. O termo deriva do japonês e junta as palavras “ori”, que significa “dobrar”, e “kami”, que é traduzido como “papel”. A técnica tradicional consiste em dobrar uma única folha de papel, quadrada, em uma escultura, sem fazer cortes ou colar o material. As principais formas encontradas nessa arte são animais, objetos, barcos e caixas.”
Naomi, em se tempo vago, trabalha na construção dos mais diversos tipos de origamis. Certo dia, ela decidiu fazer um origami em que a primeira dobradura consiste da elevação do vértice [tex]D[/tex] da folha até o ponto médio [tex]M[/tex] do lado superior, como mostrado na figura abaixo.
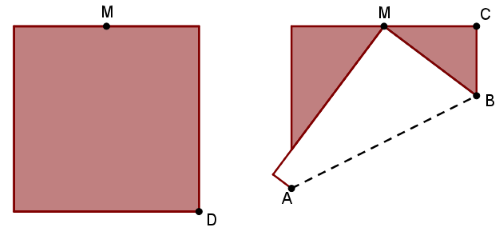
Sabendo que a área do triângulo [tex]BCM[/tex] é igual a [tex]6\;cm^2[/tex], determine a área da folha que Naomi estava utilizando.

Mas se não conseguirem, não faz mal. A partir do dia 12, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


10 comentários
Pular para o formulário de comentário
Perceba que [tex]CD=CB+BD[/tex] e que [tex]BM=BD[/tex].
Desse modo, sendo L o lado do quadrado e x a medida do segmento [tex]BD[/tex]:
Aplicando no cálculo da área de [tex]MBC[/tex]:
[tex]\dfrac{\left(\dfrac{L}{2}\right)\cdot\left(L-x\right)}=6\therefore L^2-Lx=24[/tex]
Aplicando Pitágoras em [tex]MBC[/tex]:
[tex]\left(\dfrac{L}{2}\right)^2+\left(L-x\right)^2=x^2[/tex]
Juntando as duas equações, encontramos que [tex]L^2=64[/tex], portanto a área da folha é 64cm².
Autor
Koreil Guys, vocês erraram os códigos Latex nessa primeira expressão que colocaram. Deem uma olhada.
Além disso, é importante apresentar os cálculos de porque encontraram 64 cm² de área, escrever “Juntando as duas equações, encontramos que [tex]L^2=64[/tex]” não é suficiente, é preciso provar, para que possamos nos convencer de que a afirmação de fato é verdadeira.
O que acham que resolver novamente com a correção e esses acréscimos dos cálculos?
Para esta questão conseguimos encontrar duas maneiras diferentes de resolvê-la, sendo uma com geometria e uma com álgebra, sendo assim, iremos separar nossa resposta em dois casos:
[b]Caso 1: Geometria[/b]
Na geometria, a mediana é um segmento de reta que liga um vértice de um triângulo ao ponto médio do lado oposto. Dividindo o quadrado em questão ao meio, teremos dois triângulos semelhantes, então unindo o vértice [tex]D [/tex] ao ponto médio [tex]M[/tex], temos uma mediana, sendo o triângulo [tex]MCD[/tex] um derivado do terno pitagórico primitivo [tex](3,4,5)[/tex]. Chamando [tex]\overline {MC}[/tex] de [tex]x[/tex] e [tex]\overline {CB}[/tex] de [tex]y[/tex], a área desse triângulo é definida por[tex]\frac {x \cdot y} {2} = 6[/tex], logo [tex] x \cdot y = 12[/tex]. Sendo o triângulo [tex]MCB[/tex] de área [tex]6[/tex], as possíveis medida dos catetos são,[tex] (1 \cdot 12), (2 \cdot 6), (3 \cdot 4)[/tex], como o triângulo formado [b]DEVE [/b]obedecer as proporções do triângulo Pitagórico primitivo [tex] (3,4,5)[/tex], e o cateto formado pelo ponto médio sempre será o maior cateto do triângulo formado, logo [tex]\overline {MC} = 4 [/tex] e o lado do quadrado [tex]8[/tex]. Logo, [tex]l^2=(8cm)^2=64cm^2[/tex].
[b]Caso 2: Álgebra[/b]
Primeiramente podemos observar que o ponto [tex]B[/tex] está disposto no segmento [tex]\overline {CD}[/tex], sendo assim o lado do quadrado é igual a [tex]\overline {CB} + \overline {BD}[/tex], podemos notar que após a dobradura o segmento [tex]\overline {BM}[/tex] foi sobreposto pelo segmento [tex]\overline {BD}[/tex], portanto os dois são congruentes. Chamando o lado do quadrado de [tex]l[/tex] e o segmento [tex]\overline {BM}[/tex] de [tex]x[/tex], temos que a fórmula da área do triângulo [tex]BCM[/tex] será:
[centro][tex]\frac {b \cdot h}{2} \rightarrow \frac {l}{2} \cdot (l-x) \cdot \frac {1}{2} = 6 \rightarrow \frac {l^2 – lx}{4} = 6 \rightarrow l^2 – lx = 24[/tex][/centro]
Assim descobrimos que [tex]l^2 – lx = 24[/tex]. Como sabemos que [tex]\overline {MC} = \frac {l}{2}, \overline {CB} = l – x[/tex] e [tex]\overline {BM} = x[/tex], podemos agora utilizar o teorema de Pitágoras, assim obtendo:
[centro][tex](\frac {l}{2})^2 + (l – x)^2 = x^2 \rightarrow \frac {l^2}{4} + l^2 – 2lx +\cancel {x^2} = \cancel {x^2} \rightarrow \frac {l^2 + 4l^2 – 8lx}{4} = 0 \rightarrow 5l^2 – 8lx = 0[/tex][/centro]
Analisando, vemos que encontramos duas equações, ambas com as mesmas incógnitas [tex]l^2[/tex] e [tex]lx[/tex], utilizando um sistema de equações, temos:
[centro][tex] \begin {cases}
{l^2 – lx = 24} \\
{5l^2 – 8lx =0} \\
\end {cases}[/tex][/centro]
Multiplicando a primeira equação por [tex](-8)[/tex], obteremos:
[centro][tex] \begin {cases}
{-8l^2 + \cancel 8lx = -192} \\
{5l^2 – \cancel 8lx =0} \\
\end {cases}[/tex][/centro]
Somando ambas as equações, teremos [tex]-3l^2 = -192 \rightarrow l^2 = 64[/tex], sendo [tex]64cm^2[/tex] a área do quadrado.
Autor
Pessoal, a segunda solução está muito boa. Parabéns!
Em relação a primeira solução, confesso a vocês que não está muito legal. Vocês apresentaram um conceito de mediana e não consegui ver onde vocês aplicaram o uso da mediana na solução. Um outro ponto importante é que vocês afirmaram que as medidas dos lados do triângulo BCM são derivadas do terno pitagórico (3, 4, 5), mas não entendi porque vocês chegaram a essa conclusão, uma vez que vocês não demonstraram.
A princípio, chamarelos de [tex]l[/tex] a medida do lado da folha, e de [tex]x[/tex] o segmento [tex]\overline{BC}[/tex]. sabendo que o segmento [tex]\overline{MC}[/tex] representa metade do lado da folha, ou seja, [tex]\frac{l}{2}[/tex], respectivamente, a base e a altura relativa do triângulo [tex]MCB[/tex] são [tex]\frac{l}{2}[/tex] e [tex]x[/tex]. Portanto, sua área pode ser obtida utilizando [tex](\frac{ b \cdot h}{2})[/tex], e com isso, podemos obter a seguinte informação:
$$
A = \frac{b \cdot h}{2} \Rightarrow 6 = \frac{\frac{l}{2} \cdot x}{2} \Rightarrow 6 = \frac{l \cdot x}{4} \therefore lx = 24
$$
Agora perceba que, a hipotenusa de [tex]BCM[/tex], como é uma dobra da folha inicial de lado [tex]l[/tex], quando juntamos a sua medida com o pedaço de [tex]l[/tex] equivalente a [tex]x[/tex], obtemos o lado [tex]l[/tex] novamente. Mais precisamente, podemos afirmar que [tex]x + \overline{BM} = l[/tex], que é o equivalente a dizer que [tex]\overline{BM} = l – x[/tex]. Sabendo disso, pelo teorema de Pitágoras, obtemos o seguinte:
$$
(l – x)^2 = x^2 + (\frac{l}{2})^2 \Rightarrow l^2 – 2lx + x^2 = x^2 + \frac{l^2}{4}
$$
Como já sabemos que [tex]lx = 24[/tex], podemos substituí-lo na igualdade acima, e também cancelar [tex]x^2[/tex] que aparece em ambos os lados. Assim, podemos prosseguir:
$$
l^2 – 2 \cdot (24) + \cancel{x^2} = \cancel{x^2} + \frac{l^2}{4} \Rightarrow l^2 – 48 = \frac{l^2}{4} \Rightarrow 4(l^2 – 48) = l^2 \Rightarrow 4l^2 – 192 = l^2 \Rightarrow 3l^2 = 192 \therefore l^2 = \frac{192}{3} = 64
$$
Como um quadrado de lado [tex]l[/tex] possui área igual a [tex]l^2[/tex], a área da folha que Naomi estava usando é igual a [tex]64[/tex] [tex]cm^2[/tex] :D
Autor
Muito bem, pessoal.
se a folha é quadrada, logo, o triângulo é retângulo: tendo área 6, fazendo a formula de área do triângulo ao contrário = (B×H)/2=6. B×H=12, base=4 e altura=3.
Tendo a folha como quadrado, e o triângulo é pitagóricos, temos uma figura semelhante ao quadrado que prova o teorema de Pitágoras; 4 triângulos retângulos nas extremidades, nos quais o quadrado interno é o quadrado da hipotenusa.
Devido a esta comparação, os lados medem 3+4=7. Logo a área da folha é 49 cm².
Autor
Caros, infelizmente a resposta está incorreta. O que acham de tentar novamente?
Bom dia!
Para resolvermos esse problema, vamos chamar a base de X e a altura de Y do triângulo BCM. Depois nós podemos descobrir os catetos do triângulo ultilizando a seguinte formúla: X.Y/2=6. Para descobrirmos os valores para x e y, podemos multiplicar ambos os lados da equação por 2, logo, a equação ficará x.y= 12. Agora, os possíveis valores para x e y serão 1,12; 3,4;2.6. logo, porém, os unicos valores para os catetos do triângulo BCM são 4 e 3. se subtituirmos x e y por 4 e 3 teremos um triângulo pitagórigo com as seguintes medidas,3,4 e 5.A hipotenusa desse triângulo será o segmento MB. Se somarmos 3+5 obteremos 8. logo, 8 será o lado do quadrado. agora podemos calcular a área do quadrado: 8²= 64.logo, a área do quadrado será 64.
OBS: por um obséquio, nos ajudem a utilizar latex.
Autor
Pessoal, infelizmente o argumento que vocês utilizaram não está correto. O que acham de tentar novamente?
Quanto ao Latex, no Fórum temos um tópico que pode ajudar: https://clubes.obmep.org.br/forum/viewtopic.php?f=928&t=4223