PROBLEMA
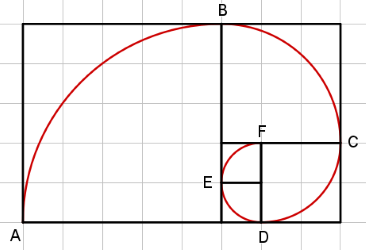
Calcule o comprimento [tex]C[/tex] da curva em vermelho abaixo, sabendo que os quadrados da malha quadriculada têm lado medindo [tex]1 \;\text{cm}[/tex] e cada um dos arcos inscritos nos quadrados possuem medida angular de [tex]90^{\circ}[/tex].

Mas se não conseguirem, não faz mal. A partir do dia 15, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


10 comentários
Pular para o formulário de comentário
A medida da curva em vermelho é equivalente à soma dos arcos AB, BC, CD, DE e EF.
O arco AB é [tex]\dfrac{1}{4}[/tex] do comprimento de uma circunferência de raio 5:
[tex]AB = 5\cdot2\cdot\pi\cdot\dfrac{1}{4}=2,5\pi[/tex]
O mesmo raciocínio se aplica aos outros arcos:
[tex]BC=1,5\pi[/tex]
[tex]CD=\pi[/tex]
[tex]DE=EF=0,5\pi[/tex]
[tex]AB+BC+CD+DE+EF=6\pi[/tex]
Interessante ressaltar que os retângulos da figura estão conforme a proporção áurea (lado = 1,1,2,3,5, …).
Ao escrever esse problema, fiquei com uma dúvida: qual o comando em [tex]latex [/tex] para colocar o sinal de arco?
Autor
Muito bem, Koreil Guys, resposta correta.
Bem observada a relação com a sequência de Fibonacci.
Quando ao código, em latex, para escrever, por exemplo, o arco AB, vocês podem estar utilizando \stackrel{\frown}{AB}.
Para calcular o comprimento da curva, como ela é composta por arcos de circunferência inscritos em quadrados, podemos utilizar a fórmula do comprimento do arco da circunferência ([tex]r \cdot \theta[/tex]), onde o raio [tex]r[/tex] destes serão iguais aos lados do quadrado o quais estão inscritos, e como todos os comprimentos representam [tex]\frac{1}{4}[/tex] de uma circunferência completa, todos os arcos menores possuem um ângulo [tex]\theta = 90º = \frac{\pi}{2}rad[/tex]. Com isso, começando pelo arco [tex]AB[/tex], indo até o arco [tex]EF[/tex], em ordem decrescente, temos:
[tex]AB = \frac{\pi}{2} \cdot 5 \Rightarrow AB = \frac{5\pi}{2}[/tex]
[tex]BC = \frac{\pi}{2} \cdot 3 \Rightarrow BC =\frac{3\pi}{2}[/tex]
[tex]CD = \frac{\pi}{2} \cdot 2 \Rightarrow CD = \pi = \frac{2\pi}{2}[/tex]
[tex]DE = EF = \frac{\pi}{2} \cdot 1 \Rightarrow DE = EF = \frac{\pi}{2}[/tex]
Agora, para calcular o comprimento [tex]C[/tex], ou seja, toda a curva em vermelho, basta somar todos os resultados obtidos:
[tex]C = AB + BC + CD + DE + EF \Rightarrow C = \frac{5\pi}{2} + \frac{3\pi}{2} + \frac{2\pi}{2} + \frac{\pi}{2} + \frac{\pi}{2}[/tex]
[tex]\Rightarrow C = \frac{12\pi}{2} = 6\pi[/tex]
Com isso, chegamos a conclusão de que, o comprimento [tex]C[/tex] da curva em vermelho possui um comprimento de [tex]6\pi[/tex] cm (aproximadamente [tex]18,85[/tex] cm)
Autor
Muito bem, Potências de Euler.
Observando a figura vimos que os arcos em vermelho são [tex]\dfrac{1}{4}[/tex] de círculo, então, vamos calcular o comprimento destes círculos, somar os resultados e por fim dividir por 4.
[tex] \stackrel{\frown}{AB}[/tex]: [tex]2\cdot\pi\cdot5[/tex] = [tex]10\pi[/tex]
[tex] \stackrel{\frown}{BC}[/tex]: [tex]2\cdot\pi\cdot3[/tex] = [tex]6\pi[/tex]
[tex] \stackrel{\frown}{CD}[/tex]: [tex]2\cdot\pi\cdot2[/tex] = [tex]4\pi[/tex]
[tex] \stackrel{\frown}{DE}[/tex]: [tex]2\cdot\pi\cdot1[/tex] = [tex]2\pi[/tex]
[tex] \stackrel{\frown}{EF}[/tex]: [tex]2\cdot\pi\cdot1[/tex] = [tex]2\pi[/tex]
Agora vamos apenas somar os resultados: [tex]10\pi+6\pi+4\pi+2\pi+2\pi= 24\pi[/tex]. E por ultimo dividimos por 4: [tex]\dfrac{24\pi}{4} = 6\pi[/tex].
Então podemos dizer que o comprimento [tex]C[/tex] tem [tex]6\pi[/tex] de comprimento.
Autor
Correto, pessoal.
Observando a figura percebemos que podemos separar as circunferências para facilitar o calculo.
Tendo no final os seguintes arcos: FE e ED(Que são iguais),DC,CB e BA.
É perceptível ver que a cada arco de circunferência pode ser julgado como 1/4 de um circulo inteiro, portanto no calculo vamos considerar o lado do quadrado aonde está inserido seu raio, já que na pratica realmente seria.
E precisamos calcular seu comprimento no caso seu perímetro, tendo como o formula 2π.R.
FE=ED
2.π.1/4 = 0.5π
DC
2.π.2/4 = π
CB
2.π.3/4= 1.5π
BA
2.π.5/4= 2,5π
FE+ED+DC+CB+BA= 0,5π+0,5π+1π+1,5π+2,5π = 6π
Portanto o comprimento das semicircunferências é igual a 6 π.
Autor
Correto, Obmépicos.
Na parte da curva com menor raio (arco FD), esta descreve uma semicircunferência de raio 1, seu comprimento é (2π×1)/2 = π
Na próxima parte (arco DC) ela é um quarto de circunferência de raio 2, logo (2π×2)/2 = π
No arco CB, ela é um quarto de circunferência de raio 3 e de B até A o comprimento é o mesmo de um quarto de circunferência de raio 5, esses comprimentos são, respectivamente: (2π×3)/4 = 1,5π e (2π×5)/4 =2,5π
Somando os 4 comprimentos encontrados, obtemos o comprimento total da curva de F até A, que é π + π + 1,5π + 2,5π = 6π.
Autor
Muito bem, pessoal.