PROBLEMA
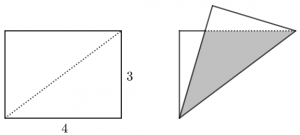
Uma folha de papel retangular medindo [tex]4[/tex] unidades de comprimento e [tex]3[/tex] unidades de altura foi dobrada ao longo da linha tracejada indicada na figura. Determine a área do triângulo sombreado.

Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
Pelo teorema de pitagoras, o quadrado da diagonal do retângulo é igual a soma total dos quadrados dos lados 4 e 3, encontrando portando que a diagonal medirá 5 unidades de comprimento.
Tendo “m” como um dos lados isoseles do triangulo sombreado, e n = 4 – m, podemos concluir, pelo teorema de pitagoras, que n = 4 – m ∴ (4 – m)² + 3² = m² ∴ 16 – 8m + m² + 3² = m² ∴ m = 25/8.
Tendo, pelo teorema de pitagoras, que o quadrado da altura do triangulo sombreado, que é perpendicular a base maior de 5 unidades de comprimento, será, quando somado ao quadrado da metade do maior lado do triangulo sombreado, que é (2,5)², igual ao valor de m², portanto m² = (2,5)² + h² ∴ h² = (-6,25) + (25/8)² ∴ h = √(3,515625) ∴ h = 1,875. Tendo a área do triangulo igual a (Altura×Base)/2, conclui-se que (1,875×5)/2 = (Área do triangulo sombreado) ∴ Área do triangulo sombreado = 4,6875.
∴ = “Portanto”
Autor
A solução está correta Matemáticos do Agnus Dei, parabéns! Faltou apenas justificar a razão do triângulo sombreado ser isósceles.