PROBLEMA
Considere os quadrados dispostos como na figura:
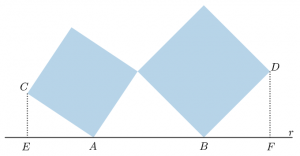
Sabendo-se que a distância do ponto [tex]C[/tex] à reta [tex]r[/tex] é de [tex]2[/tex] cm e que a distância do ponto [tex]D[/tex] à reta [tex]r[/tex] é de [tex]3[/tex] cm, calcule a medida do segmento [tex]\overline{AB}[/tex].
Mas se não conseguirem, não faz mal. A partir do dia 24, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
Primeiramente, vamos denotar de [tex]p[/tex] o ponto de encontro dos vértices dois quadrados, e os ângulos [tex]\angle EAC = \alpha[/tex], [tex]\angle FBD = \beta[/tex], [tex]\angle pAB = \gamma[/tex] e [tex]\angle pBA = \delta[/tex]. Após isso, tomemos o ponto [tex]p'[/tex] na reta [tex]r[/tex], de forma que o segmento [tex]\overline {pp’}[/tex] seja perpendicular a reta [tex]r[/tex]. Perceba que, este segmento divide o triângulo de lado [tex]AB[/tex] em dois outros triângulos retângulos em [tex]p'[/tex]. Agora, para resolução do problema, vamos utilizar o teorema do ângulo externo: o ângulo externo de um triângulo é igual à soma dos dois ângulos internos não adjacentes a ele. Outra forma mais “simples” de visualizar, é dizer que, o suplementar de um ângulo interno de um triângulo (isto é, o ângulo que falta para que se complete um ângulo de [tex]180º[/tex]) é igual a soma dos dois outros ângulos internos deste triângulo. Agora, vamos fazer a seguinte visualização:
O suplementar do ângulo [tex]\gamma[/tex] é igual a [tex]90 + \alpha[/tex], ou seja, pelo teorema do ângulo externo, a soma dos outros dois ângulos de [tex]pp’A[/tex] é igual a [tex]90+ \alpha[/tex]. Perceba que, como este é um triângulo retângulo, necessariamente, já sabemos que os [tex]90º[/tex] estão no ângulo em [tex]p'[/tex], portanto, o ângulo [tex]App'[/tex] é igual a [tex]\alpha[/tex]. Pelo caso [tex]ALA[/tex] (considerando o lado do quadrado em comum), os triângulos [tex]CEA[/tex] e [tex]App'[/tex] são congruentes, logo, o lado oposto ao ângulo [tex]\alpha[/tex] é igual a [tex]CE = Ap’ = 2 \ cm[/tex].
Analogamente, sabendo que o suplementar de [tex]\delta[/tex] é igual a [tex]90 + \beta[/tex], encontramos que, o ângulo [tex]p’pB[/tex] é igual a [tex]\beta[/tex], e que os triângulos [tex]BFD[/tex] e [tex]Bpp'[/tex] são congruentes pelo caso [tex]ALA[/tex] (considerando o lado do quadrado em comum). Como sabemos, o lado oposto ao ângulo [tex]\beta[/tex] é igual a [tex]DF = Bp’ = 3 \ cm[/tex].
Como [tex]\overline{AB} = Ap’ + Bp'[/tex], podemos concluir que, o segmento [tex]\overline{AB}[/tex] é igual a [tex]2 + 3 = 5 \ cm[/tex] :D
Autor
A solução está correta Potências de Euler. Parabéns!