PROBLEMA
Em uma malha quadriculada [tex]1\times 1[/tex] foram construídas as figuras [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] abaixo.
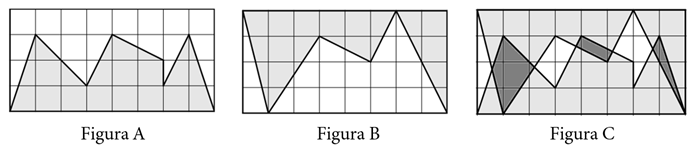
Calcule a área branca da figura [tex]C[/tex], sabendo que a área mais escura de [tex]C[/tex] vale [tex]4[/tex].

Mas se não conseguirem, não faz mal. A partir do dia 17, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas. do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
Veja que, se a área mais escura de C, correspondente à intercessão entre as áreas cinzas de A e B, vale 4, então a área cinza de C é a soma das áreas cinzas de A e B, menos 4. Logo, a área branca de C é o total, [tex]4\times 8 = 32[/tex], menos a área cinza de C.
Estabelece-se um sistema de coordenadas, com origem no canto inferior esquerdo de cada figura, com 1 unidade equivalente a um lado de quadradinho.
Na figura A:
A área cinza total é a soma das áreas dos polígonos determinados pelos pontos:
1 – (0,0), (1,0), (1,3); A área é [tex]\dfrac{1\times 3}{2}[/tex]
2 – (1,0), (1,1), (7,1), (7,0); A área é [tex]6\times 1[/tex]
3 – (1,1), (1,3), (3,1); A área é [tex]\dfrac{2\times 2}{2}[/tex]
4 – (3,1), (4,1), (4,3); A área é [tex]\dfrac{1\times 2}{2}[/tex]
5 – (4,3), (4,2), (6,2); A área é [tex]\dfrac{2\times 1}{2}[/tex]
6 – (4,1), (4,2), (5,1), (5,2); A área é [tex]2\times 1[/tex]
7 – (6,1), (7,1), (7,3); A área é [tex]\dfrac{1\times 2}{2}[/tex]
8 – (7,3), (7,0), (8,0); A área é [tex]\dfrac{1\times 3}{2}[/tex]
Logo, a área é [tex]\dfrac{3 + 4 + 2 + 2 + 2 + 3}{2} + 6 + 2 = 16[/tex].
Na figura B:
A área cinza total é a soma das áreas dos polígonos determinados pelos pontos:
1 – (0,4), (1,4), (1,0); A área é [tex]\dfrac{1\times 4}{2}[/tex]
2 – (1,4), (5,4), (1,3), (5,3); A área é [tex]4\times 1[/tex]
3 – (1,3), (1,0), (3,3); A área é [tex]\dfrac{2\times 3}{2}[/tex]
4 – (3,3), (5,3), (5,2); A área é [tex]\dfrac{1\times 2}{2}[/tex]
5 – (5,2), (5,4), (6,4); A área é [tex]\dfrac{2\times 1}{2}[/tex]
6 – (6,4), (8,4), (8,0); A área é [tex]\dfrac{4\times 2}{2}[/tex]
Logo, a área é [tex]\dfrac{4 + 6 + 2 + 2 + 8}{2} + 4 = 15[/tex].
Portanto, a área cinza de C é [tex]15 + 16 – 4 = 27[/tex], logo a resposta é que a área branca da figura C mede [tex]32 – 27 = 5[tex].
Autor
Trabalharam muito, mas trabalharam bem.
Parabéns!