PROBLEMA
A figura seguinte mostra um triângulo retângulo [tex]ABC[/tex]. O ponto [tex]M[/tex] é o ponto médio do lado [tex]\overline{AB}[/tex], que é a hipotenusa.
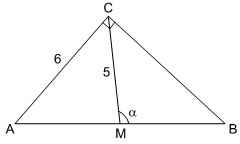
Calcule o valor de [tex]cos\alpha[/tex].
Reúnam seus Clubes e tentem resolver o problema.
Mas se não conseguirem, não faz mal. A partir do dia 8, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Mas se não conseguirem, não faz mal. A partir do dia 8, próxima quinta-feira, deem uma passadinha na Sala Problemas de 2024: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!
2 comentários
Inicialmente, iremos considerar [tex]AM = MB = x[/tex], então [tex]AB = 2x[/tex].
Aplicando o Teorema de Pitágoras no triângulo [tex]ABC[/tex], tem-se que [tex]CB^2= 4x^2 – 6^2[/tex].
Utilizando o teorema de Stewart no triângulo [tex]ABC[/tex], tem-se que [tex]AC^2 \cdot MB + BC^2 \cdot AM = AB \cdot CM^2 + AM \cdot MB \cdot AB[/tex].
Substituindo valores, temos que
[centro][tex]6^2 \cdot x + (4x^2 – 6^2) \cdot x = 2x \cdot 5^2 + x \cdot x \cdot 2x \Rightarrow[/tex]
[tex] 6^2 \cdot x + 4x^3 – 6^2 \cdot x = 50 \cdot x + 2x^3 \Rightarrow 2x^3 = 50 \cdot x \Rightarrow [/tex]
[tex]x^2 = 25 \Rightarrow x=5[/tex][/centro]
Assim, [tex]CB^2= 4x^2 – 6^2 = 4 \cdot 5^2 – 36 = 64[/tex]
Utilizando a Lei dos Cossenos no triângulo [tex]MBC[/tex] em relação ao ângulo [tex]\alpha[/tex], temos que
[centro][tex]CB^2 = CM^2 + MB^2 – 2 \cdot CM\cdot MB \cdot cos\alpha[/tex]
[tex]64 = 5^2 + 5^2 – 2\cdot 5\cdot 5 \cdot cos \alpha[/tex]
[tex]64 = 50 – 50 \cdot cos\alpha[/tex]
[tex]cos\alpha = -\frac{14}{50}=-\frac{7}{25}[/tex][/centro]
Dessa forma, conclui-se que [tex]\boxed{cos\alpha = -\frac{7}{25}}[/tex]
Autor
Parabéns pela participação, ALIANÇA ARQUIMEDIANA.
A solução está correta.
No nosso fórum há uma dica que pode levar a uma solução diferente sem a relação de Stewart.
Podem passar por lá e encontrarem um outro caminho.