PROBLEMA
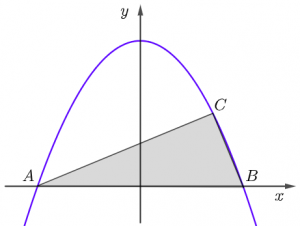
A curva da figura é dada pela equação [tex]y=-x^2+4[/tex] e o triângulo [tex] ABC[/tex] é retângulo com ângulo reto no vértice [tex]C[/tex]. Calcule a área deste triângulo.

Mas se não conseguirem, não faz mal. A partir do dia 4, próxima quinta-feira, deem uma passadinha na Sala Problemas: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
Colocando as respectivas coordenadas dos pontos temos:
[tex]A:(-2;0)[/tex] [tex] \ [/tex] [tex]B:(2;0)[/tex] [tex] \ [/tex] [tex]C:(x; -x^2+4)[/tex]
Adicionando um ponto [tex]M[/tex] de coordenada [tex](x;0)[/tex]
Temos os triângulos retângulos, com suas respectivas relações pitagóricas:
[tex](I)\triangle ABC \Rightarrow AB^2=BC^2+AC^2[/tex]
[tex](II)\triangle ACM \Rightarrow AC^2=AM^2+CM^2[/tex]
[tex](III)\triangle BCM \Rightarrow BC^2=BM^2+CM^2[/tex]
Inserindo [tex](II)[/tex] e [tex](III)[/tex] em [tex](I)[/tex] temos:
[tex](IV)AB^2=AM^2+BM^2+2CM^2[/tex]
Descobrindo o valor de cada segmento pelos seus pontos temos:
[tex]AB=4[/tex]
[tex]AM=2+x[/tex]
[tex]BM=2-x[/tex]
[tex]CM=-x^2+4[/tex]
Substituindo em [tex](IV)[/tex] ficaremos com a seguinte seguinte biquadrada:
[tex]x^4-7x^2+12=0[/tex]
Que tem as raízes [tex]\pm2[/tex] e [tex]\pm\sqrt{3}[/tex]
As raízes [tex]\pm2[/tex] não será considerada pois seriam os pontos [tex]A[/tex] e [tex]B[/tex]
Logo com [tex]x=\pm\sqrt{3}[/tex] temos a altura do triangulo [tex]-(\pm\sqrt{3})^2+4=1[/tex] a base [tex]AB=4[/tex] a área é igual a [tex]2[/tex] Unidade de Área.
Autor
Parabéns Sociedade dos termos variados, a solução está correta.