PROBLEMA
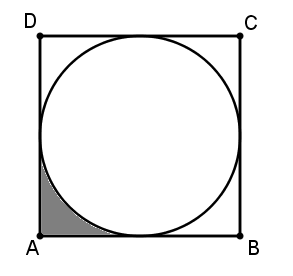
Determine o raio da circunferêcia inscrita no quadrado ABCD abaixo, sabendo que a área da região sombreada é [tex]2 ~cm^2[/tex].

Mas se não conseguirem, não faz mal. A partir do dia 18, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


2 comentários
[textarea]A princípio, denotaremos por [tex]l[/tex] a medida do lado do quadrado, e [tex]R[/tex] o raio da circunferência. Traçando um raio [tex]R[/tex] perpendicular a qualquer um dos lados [tex]l[/tex], é trivial que o raio equivale a metade do lado do quadrado ([tex]R = \frac{l}{2} \Rightarrow 2R = l[/tex]). Sabendo disso, podemos escrever o valor da área sombreada seguindo a seguinte expressão, utilizando os termos [tex]\frac{l^2}{4}[/tex], que representa [tex]\frac{1}{4}[/tex] da área do quadrado, que também é igual ao quadrado menor de lados [tex]R[/tex], onde está a área sombreada de [tex]ABCD[/tex], e [tex]\frac{\pi R^2}{4}[/tex], que representa [tex]\frac{1}{4}[/tex] do círculo inscrito no quadrado [tex]ABCD[/tex], que também é igual ao setor círcular do quadrado menor onde está a área sombreada. Não é difícil perceber que, a área sombreada equivale a área deste quadrado menor de lado [tex]R[/tex] subtraído do setor circular que está nele. Portanto, podemos reescrever a área sombreada [tex]A_s[/tex] como:
[tex]A_s = A_{quadrado} – A_{setor} \Rightarrow 2 = \frac{l^2}{4} – \frac{\pi R^2}{4}[/tex]
Como sabemos que [tex]l = 2R[/tex], podemos proceder da seguinte maneira:
[tex]2 = \frac{l^2}{4} – \frac{\pi R^2}{4} \Rightarrow 2 = \frac{(2R)^2}{4} – \frac{\pi R}{4} \Rightarrow 2 = \frac{4 R^2}{4}- \frac{\pi R^2}{4} \Rightarrow 2 = \frac{4 R^2 – \pi R^2}{4} \Rightarrow 2 = \frac{R^2(4- \pi)}{4} \Rightarrow R^2 = \frac{8}{4- \pi} \therefore R = \sqrt{\frac{8}{4 – \pi}} = \frac{2 \sqrt{2}}{\sqrt{(4 – \pi)}}[/tex]
Assim, concluímos que o raio da circunferência inscrita é igual a [tex]\frac{2 \sqrt{2}}{\sqrt{(4 – \pi)}}[/tex] :D
[/textarea]
Autor
Muito bem, Potências de Euler. Excelente resolução!