jul 22

Prisma Planificado

PROBLEMA

No dia [tex]28[/tex] de junho, o Colégio Militar de Fortaleza promoveu o “Dia do Alívio”, uma atividade que contou com apresentações artísticas dos alunos do colégio, que teve como objetivo proporcionar um momento de integração, descontração e fortalecimento de vínculos fraternos entre os alunos. Essa atividade foi realizada em um palco, em forma de prisma, que pode ser planificado conforme representado a seguir.

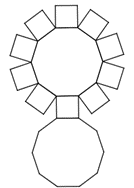
Por curiosidade, um aluno do [tex]6^\circ[/tex] ano resolveu contar o número de faces [tex](F)[/tex], o número de arestas [tex](A)[/tex] e o número de vértices [tex](V)[/tex] desse prisma, e posteriormente, efetuou as seguintes operações [tex](V\times F)\div A[/tex]. Qual o valor obtido?

Reúnam seus Clubes e tentem resolver o problema.
Mas se não conseguirem, não faz mal. A partir do dia 25, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas. do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!

Bons estudos, pessoal!

Link permanente para este artigo: http://clubes.obmep.org.br/blog/2024/07/prisma-planificado/

5 comentários

Pular para o formulário de comentário

  1. Boa noite!

    Não sabemos se aqui é o local adequado para a postagem de resoluções, já que não possui a interface do Latex. Somos um clube novo e ainda não possuímos acesso ao fórum, mas gostaríamos de interagir.

    Um prisma pode ser entendido como um poliedro formado pela união dos vértices de dois polígonos convexos congruentes (bases) por meio de arestas em um plano perpendicular ao dos polígonos.

    Por essa interpretação, podemos inferir o seguinte:

    1. O número de faces de um prisma é então (L+2) sendo L a quantidade de lados do polígono da base.

    2. O número de vértices de um prisma é 2V’ sendo V’ a quantidade de vértices do polígono da base. Como, em um polígono convexo o número de vértices é igual ao número de lados, podemos expressar a quantidade de vértices no prisma como 2L.

    Pela Relação de Euler para os Poliedros convexos, tem-se que F + V = A + 2, portanto A = F + V – 2 = 3L

    Realizando a operação V x F / A, temos:

    V x F / A = (L+2) x 2L / 3L = 2(L+2)/3

    No caso do problema, é um decágono:

    2(10+2)/3 = 8

    1. Boa tarde, pessoal! Podem utilizar o [tex]\LaTeX[/tex] no Blog sim, basta colocar o código entre tags [tex] [/tex]. Bem-vindos!

  2. Que legal gente! Parabéns pela solução!
    A solução foi muito criativa.
    Apenas uma observação em uma parte da escrita de vocês:

    “Um prisma pode ser entendido como um poliedro formado pela união dos vértices de dois polígonos convexos congruentes (bases) por meio de arestas em um plano perpendicular ao dos polígonos.”

    As arestas não precisam ser perpendiculares aos polígonos (prisma oblíquo).

    A solução de vocês em breve será publicada.

    Continuem trabalhando.

  3. Para resolver a questão de forma mais rápida e objetiva, contamos a quantidade de vértices, sendo [tex]10[/tex] na base, por ser um decágono, e [tex]10[/tex] na face superior, sendo assim temos [tex]20[/tex] vértices no total. Para fazer a contagem das faces, contamos uma superior, uma inferior e [tex]10[/tex] nas laterais, totalizando [tex]12[/tex]. Agora, conseguimos descobrir a quantidade de arestas por meio da relação de Euler para poliedros convexos:

    [tex]V – A + F = 2[/tex]
    [tex]20 – A + 12 = 2[/tex]
    [tex]-A = -30 [/tex]
    [tex]A = 30[/tex]

    Ou seja, [tex]12[/tex] faces, [tex]30[/tex] arestas e [tex]20[/tex] vértices. Agora, para descobrir o valor que o aluno achou, basta seguir as operações que ele realizou:

    [tex]\frac{(20 \cdot 12)}{30} \Rightarrow \frac{2 \cdot 12}{3} \Rightarrow \frac{24}{3} = 8[/tex]

    Assim, concluímos que o valor obtido pelo aluno foi [tex]8[/tex] :D

    1. Joia.

Deixe uma resposta