PROBLEMA
Na figura a seguir, cada triângulo e o quadrado central possui um número natural oculto.
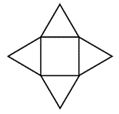
Em cada uma das situações a seguir, o número que aparece embaixo de cada figura é a soma dos números que estão nos triângulos sombreados e no quadrado central sombreado.
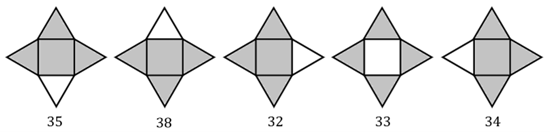
Qual o número oculto do quadrado que satisfaz as condições acima?
Reúnam seus Clubes e tentem resolver o problema.
Mas se não conseguirem, não faz mal. A partir do dia 27, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas. do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Mas se não conseguirem, não faz mal. A partir do dia 27, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas. do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!
2 comentários
Nomeando o número do triângulo superior com a variável [tex]A[/tex], da direita com a variável [tex]B[/tex], de baixo com a variável [tex]C[/tex], da esquerda com a variável [tex]D[/tex] e do quadrado com a variável [tex]E[/tex], segundo o enunciado, chegamos as seguintes equações:
I ) [tex]A + B + D + E = 35[/tex]
II ) [tex]B + C + D + E = 38[/tex]
III ) [tex]A + C + D + E = 32[/tex]
IV ) [tex]A + B + C + D = 33[/tex]
V ) [tex]A + B + C + E = 34[/tex]
Somando todas estas cinco equações, chegamos em:
[tex]4A + 4B + 4C + 4D + 4E = 172[/tex]
[tex]4 \cdot (A + B + C + D + E) = 4 \cdot 43[/tex]
[tex] A + B + C + D + E = 43[/tex]
Como nosso objetivo é encontrar o valor de [tex]E[/tex], isolamos ele em um lado da igualdade, o que nos resulta em:
[tex]E = 43 – (A + B + C + D)[/tex]
Agora, pela equação [b]IV[/b], nós já sabemos que [tex]A+B+C+D = 33[/tex]. Portanto, prosseguimos:
[tex]E = 43 – 33 \therefore E = 10[/tex]
Assim, chegamos a conclusão que, o número que está oculto no quadrado é [tex]10[/tex]
Autor
Maravilha!