PROBLEMA
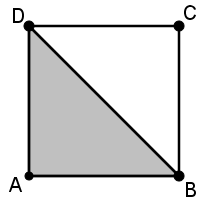
Determine a área do quadrado [tex]ABCD[/tex], sabendo que o perímetro do triângulo [tex]ABD[/tex] é igual a [tex]4~cm[/tex].

Reúnam seus Clubes e tentem resolver o problema.
Mas se não conseguirem, não faz mal. A partir do dia 20, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Mas se não conseguirem, não faz mal. A partir do dia 20, próxima quinta-feira, deem uma passadinha na Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações para tentarem resolver o problema e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Resolvido o problema, vocês podem postar suas soluções no Blog para que todos tenham acesso a elas!
Bons estudos, pessoal!


5 comentários
Pular para o formulário de comentário
Bom dia, tudo bem?
Primeiramente, vamos “achar” os lados do triângulo. Chamando o lado do quadrado de L, temos que os dois catetos do triângulo são L também, e que a hipotenusa é L√2 (diagonal do quadrado).
Agora vamos descobrir qual a medida de L:
L + L + L√2 = 4
2L + L√2 = 4
L ( 2 + √2) = 4
L = 4 / 2 +√2
Descobrindo isso, vamos substituir na fórmula da área do quadrado:
L x L =
(4 / 2 +√2) x (4 / 2 +√2) =
16 / 4 + 4√2 + 2 =
16 / 6 + 4√2
Racionalizando, temos:
(16 / 6 + 4√2) x ( 6 – 4√2 / 6 – 4√2) =
16 ( 6 – 4√2) / 36 – 16 x 2 =
16 (6 – 4√2) / 4 =
4 ( 6 – 4√2) =
24 – 16√2
Portanto, a área do quadrado é 24 – 16√2.
OBS: Não lembramos como usar o LaTex, por isso utilizamos (/) como divisão.
Autor
Muito bem, Equipe Fibonacci. Quanto ao código para escrever, por exemplo, a fração [tex]\dfrac{a}{b}[/tex], é \dfrac{a}{b}.
Ah sim, muito obrigada!
Sendo [tex]l[/tex] o lado do quadrado [tex]ABCD[/tex], a sua diagonal, que também é um dos lados de [tex]ABD[/tex], vale [tex]l \sqrt{2}[/tex], e sua área é igual a [tex]l^2[/tex]. O perímetro do triângulo pode ser obtido somando a medida de todos os seus lados, ou seja, [tex]l + l + l \sqrt{2}[/tex]. Como temos a informação de que seu perímetro é igual a [tex]4[/tex] [tex]cm[/tex], podemos partir desta igualdade para obtermos o valor de [tex]l[/tex]:
[tex]l + l + l \sqrt{2} = 4 \Rightarrow 2l + l \sqrt{2} = 4 \Rightarrow l(2 + \sqrt{2}) = 4 \therefore l = \frac{4}{2 + \sqrt{2}}[/tex]
Utilizando radiciação, para facilitar os cálculos…
[tex]l = \frac{4}{2 + \sqrt{2}} \cdot \frac{2 – \sqrt{2}}{2 – \sqrt{2}} \Rightarrow l = \frac{4(2 – \sqrt{2})}{2^2 – {\sqrt{2}}^2} \Rightarrow l = \frac{8 – 4\sqrt{2}}{4 – 2} \Rightarrow l = \frac{8 – 4\sqrt{2}}{2} \therefore l = 4 – 2 \sqrt{2}[/tex]
Por fim, agora podemos encontrar a área do quadrado:
[tex]l^2 = (4 – 2\sqrt{2})^2 \Rightarrow l^2 = 4^2 – 2 \cdot 4 \cdot (2\sqrt{2}) + (2\sqrt{2})^2 \Rightarrow l^2 = 16 – 16\sqrt{2} + 8 \therefore l^2 = 24 – 16 \sqrt{2}[/tex]
Assim, concluímos que, a área deste quadrado é igual a [tex]24 – 16 \sqrt{2}[/tex] [tex]cm^2[/tex] :D
Autor
Muito bem, Potências de Euler.