Categoria: Geometria

mar 16

Tempo para ir ao banheiro

PROBLEMA Em uma aula de Matemática, um aluno pediu para ir ao banheiro exatamente às [tex]08[/tex]h[tex]20[/tex]min. O professor, para testar o conhecimento do aluno, respondeu que ele poderia ir na próxima vez que os ponteiros dos minutos e das horas formassem um ângulo de [tex]75^\circ[/tex]. Depois de quanto tempo o aluno estará liberado para ir …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/03/tempo-para-ir-ao-banheiro/

mar 08

Paralelas

PROBLEMA Na figura abaixo, [tex]r \parallel s[/tex]. Determine a medida de [tex]\alpha[/tex] e [tex]\beta[/tex]. Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 12, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum. Lá vocês encontrarão Dicas e Orientações que …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/03/paralelas/

fev 23

Desafio: Circunferência Tangente

PROBLEMA Considere a seguinte malha [tex]4\times 4[/tex] de quadrados com lado unitário e três circunferências [tex]\Omega_1, \Omega_2, \Omega_3[/tex]. Qual é o raio da circunferência [tex]\Omega[/tex] que tangencia as outras três? Reúnam seus Clubes e tentem resolver o problema. Caso não consigam, não se preocupem. A partir do dia 26, próxima quinta-feira, visitem a Sala Problemas …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/02/desafio-circunferencia-tangente/

fev 16

Problemão: Mais uma área máxima

PROBLEMA Deseja-se construir uma piscina em um terreno retangular com lados medindo [tex]x[/tex] e [tex]y[/tex]. A parte do terreno disponível para a construção da piscina tem o formato de um triângulo retângulo de lados 6, 8 e 10 metros. A piscina deve ser construída de forma que um de seus lados esteja sobre a hipotenusa …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/02/problemao-mais-uma-area-maxima/

nov 17

Rotacionando um retângulo

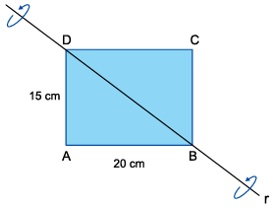
PROBLEMA O retângulo [tex]ABCD[/tex], com [tex]AB=20[/tex] [tex]cm[/tex] e [tex]AD=15[/tex] [tex]cm[/tex], será espacialmente girado de [tex]180^\circ[/tex], tendo como eixo de rotação a reta [tex]r[/tex], que passa por seus vértices [tex]B[/tex] e [tex]D[/tex], como mostra a figura. Calcule o volume do sólido espacial gerado após essa rotação. Reúnam seus Clubes e tentem resolver o problema. Caso não …

Continue lendo

Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/11/rotacionando-um-retangulo/