abr 06
PROBLEMA Uma fábrica constrói estruturas metálicas tridimensionais como mostra a ilustração. Cada uma das unidades metálicas que forma os lados dos quadrados e os pés das estruturas possui [tex]1[/tex] m de comprimento. Seguindo o padrão de construção, qual o número da estrutura metálica cuja construção utilizará [tex]224[/tex] m de metal? Reúnam seus Clubes e tentem …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/04/estruturas-metalicas/
fev 16
PROBLEMA Deseja-se construir uma piscina em um terreno retangular com lados medindo [tex]x[/tex] e [tex]y[/tex]. A parte do terreno disponível para a construção da piscina tem o formato de um triângulo retângulo de lados 6, 8 e 10 metros. A piscina deve ser construída de forma que um de seus lados esteja sobre a hipotenusa …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2026/02/problemao-mais-uma-area-maxima/
out 27
PROBLEMA Um teste envolvendo o funcionamento da memória de um grupo com muitos indivíduos foi realizado da seguinte forma: foram criados vários cartões contendo em cada um uma imagem e um número associado a ela. Cada uma das pessoas foi exposta a estes cartões por um tempo [tex]t[/tex], em minutos, e em seguida recebeu um …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/experimento-e-memoria/
out 06
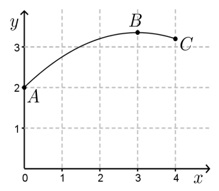
PROBLEMA Em um jogo de vôlei, o levantador de um time toca a bola no ponto [tex]A[/tex] quando ela está a [tex]2[/tex] metros de altura do chão e faz um levantamento paralelo à rede, acionando um de seus atacantes. A bola perfaz uma trajetória parabólica, como esboçado na figura abaixo, atingindo seu ponto mais alto …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/10/bola-de-volei/
set 29
PROBLEMA Uma criança nasceu com [tex]50[/tex] cm de altura e após [tex]1[/tex] ano estava com [tex]75[/tex] cm. Consideremos que a fórmula [tex]\qquad{H(t)=A+B\text{ log } (1+t)}[/tex], modela a altura [tex]H[/tex] de uma pessoa, em cm, em função de sua idade [tex]t[/tex], em anos, onde [tex]t \leq 12[/tex]. Além disso, [tex]A[/tex] e [tex]B[/tex] são constantes reais que …
Link permanente para este artigo: https://clubes.obmep.org.br/blog/2025/09/crescimento-humano/
Se você utiliza equipamentos da Apple, por favor, leia esta mensagem.