PROBLEMA
O primeiro trajeto de um robô consiste em partir do ponto [tex]P[/tex], ir até o ponto [tex]P_1[/tex] e retornar ao ponto [tex]P[/tex], percorrendo [tex]50\ m[/tex]. No segundo trajeto deve ir do ponto [tex]P[/tex] ao ponto [tex] P_2[/tex] e retornar novamente ao ponto [tex]P[/tex], percorrendo desta vez [tex]60\ m[/tex] e, assim sucessivamente.
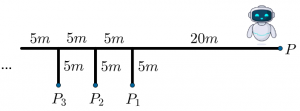
Sabendo que o robô tem bateria para percorrer uma distância de [tex]1\,800\ m[/tex], determine a quantidade de trajetos completos que ele poderá realizar.

Caso não consigam, não se preocupem. A partir do dia 30, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações que ajudam a resolver a questão e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Após resolverem o problema, compartilhem suas soluções no Fórum ou aqui no Blog, para que todos possam ter acesso a elas!
Bons estudos, pessoal!


2 comentários
Para resolvermos este problema, vamos utilizar duas fórmulas, sendo elas: [tex]S_n=\frac{(a_1+a_n)\cdot n}{2}[\tex] e [tex]a_n=a_1+(n-1)\cdot r[\tex] Elas são: Soma dos termos de uma PA e a Fórmula do termo geral de uma PA, respectivamente. Sabendo disso vamos apenas substituir os valores, e então encontrar o resultado desejado. [tex]1800=\frac{(50+(50+(n-1)\cdot10))\cdot n}{2}\Rightarrow1800=\frac{(90+10n)\cdot n}{2}\Rightarrow1800=\frac{90n+10n^2}{2}\Rightarrow 5n^2+45n-1800=0\Rightarrow n^2+9n-360=0[\tex] Aplicando a Fórmula de Bhaskara: [tex]n=\frac{-9\pm\sqrt{9^2-4\cdot1\cdot(-360)}}{2\cdot1}\Rightarrow n=\frac{-9\pm\sqrt{1521}}{2}\Rightarrow n=\frac{-9\pm39}{2}\rightarrow n_1=\frac{-9+39}{2}=15; n_2=\frac{-9-39}{2}=-24[\tex] Como é impossível o resultado ser negativo, descartamos o [tex]n_2[\tex], deste modo, afirmamos que o resultado é 15, portanto o robô consegue fazer até 15 trajetos completos.
Autor
A resposta está correta. Parabéns para Os Matemágicos!!