PROBLEMA
Após o fim de uma competição esportiva, os vencedores foram encaminhados para o pódio. Os organizadores da competição construíram um pódio no qual a posição mais alta possui a forma de um cubo e as posições inferiores são paralelepípedos retângulos conforme figura. As dimensões indicadas estão todas na mesma unidade de medida.
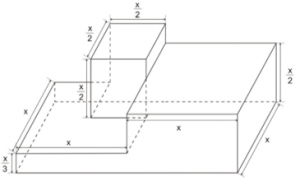
Depois de construído, o pódio deverá ser pintado, com exceção da parte inferior que estará apoiada no solo.
Encontre a expressão quer representa a área a ser pintada, em função de [tex]x[/tex].
Reúnam seus Clubes e tentem resolver o problema.
Caso não consigam, não se preocupem. A partir do dia 11, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações que ajudam a resolver a questão e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Após resolverem o problema, compartilhem suas soluções no Fórum ou aqui no Blog, para que todos possam ter acesso a elas!
Caso não consigam, não se preocupem. A partir do dia 11, próxima quinta-feira, visitem a Sala Problemas da Semana: Dicas, Orientações e Dúvidas do nosso Fórum.
Lá vocês encontrarão Dicas e Orientações que ajudam a resolver a questão e também poderão postar as suas dúvidas para que os nossos Moderadores possam lhes ajudar.
Após resolverem o problema, compartilhem suas soluções no Fórum ou aqui no Blog, para que todos possam ter acesso a elas!
Bons estudos, pessoal!
2 comentários
Para a resolução do problema, vamos analisar por partes:
Para o cubo de lado [tex]\frac{x}{2}[\tex] temos: [tex]4 \cdot \left( \frac{x}{2} \right)^2 + \frac{x}{2} \cdot \left( \frac{x}{3} + \frac{x}{2} – \frac{x}{2} \right) = \frac{7x^2}{6}[\tex].
Para o paralelepípedo [tex]x[\tex] por [tex]x[\tex] por [tex]\frac{x}{3}[\tex] temos: [tex]3 \cdot \frac{x}{3} \cdot x + x \cdot \frac{x}{2} + \left( \frac{x}{2} \right)^2 = \frac{7x^2}{4}[\tex]
Para o paralelepípedo [tex]x[\tex] por [tex]x[\tex] por [tex]\frac{x}{2}[\tex] temos: [tex]x^2 + x \cdot 3 \cdot \frac{x}{2} + \frac{x}{2} \cdot \left( \frac{x}{2} – \frac{x}{3} \right) = \frac{31x^2}{12}[\tex]
Somando os três resultados: [tex]\frac{7x^2}{6} + \frac{7x^2}{6} + \frac{7x^2}{6} = \frac{132x^2}{24} = \frac{22x^2}{4}[\tex] ou [tex]5,5x^2[\tex]
Ou seja, a expressão que utilizaremos para calcular a área pintada a partir do valor de x, é [tex]\frac{22x^2}{4}[\tex] ou [tex]5,5x^2[\tex]
Autor
Parabéns, os Matemágicos.
Solução correta!