
|
Antes de iniciar a leitura dessa Sala de Estudos, sugerimos fortemente que você dê uma passadinha na Sala de Matrizes, neste link.
|
Na Matemática ocidental antiga não se tem muitos registros de sistemas de equações lineares, diferente do Oriente, onde o assunto já era mais discutido entre os chineses, que representavam os sistemas lineares por meio de seus coeficientes escritos com barras de bambu sobre os quadrados de um tabuleiro. Acredita-se que, com essa forma de representação, eles acabaram descobrindo o método de resolução de sistemas por eliminação – anulação dos coeficientes por meio de operações básicas. Exemplos de como era realizado esse procedimento encontram-se em Os Nove Capítulos da Arte Matemática, um texto que data aproximadamente de 200 a.C. a 100 a.C.
 Uma página de Os nove capítulos da arte matemática. Imagem extraída de Wikipédia.
Uma página de Os nove capítulos da arte matemática. Imagem extraída de Wikipédia.
Na Europa, os determinantes de matrizes de ordem 2 foram estudados pelo matemático italiano Girolamo Cardano (1501 – 1576), no final do século XVI.
No Japão, a noção de determinante apareceu em 1683, através do estudo de sistemas lineares, num trabalho do matemático Seki Takakazu (1642 – 1708), também conhecido como Seki Kōwa. Dez anos depois, Gottfried Wilhelm Leibniz (1646 – 1716) introduziu o uso de determinantes no Ocidente.
No século XVIII, outros matemáticos, como Cramer, Bézout, Laplace e Vandermonde também publicaram artigos sobre determinantes e deixaram contribuições importantes, algumas das quais veremos mais adiante.
O termo determinante, com o sentido atual, surgiu em 1812 num trabalho de Augustin-Louis Cauchy (1789 – 1857), onde ele reprovou os resultados anteriores e apresentou novos resultados, simplificou o que era conhecido até então sobre determinantes e apresentou uma segunda demonstração do teorema da multiplicação de determinantes.
Em 1841, Arthur Cayley (1821 – 1895) publicou a primeira contribuição inglesa para a teoria dos determinantes. Em seu artigo, ele usou duas linhas verticais em cada lado da matriz para denotar o determinante, uma notação que agora se tornou padrão, bem como explorou propriedades e aplicações dos determinantes.
O estudo de determinantes é importante em várias áreas da Matemática e de suas aplicações práticas. Abaixo vemos alguns campos onde são aplicados determinantes.
➤ Geometria Analítica: Determinantes são usados na geometria analítica para calcular áreas de paralelogramos e volumes de paralelepípedos, bem como para verificar a coplanaridade de pontos no espaço.
➤ Teoria dos Números: Determinantes estão presentes em algumas formulações e teoremas na teoria dos números, especialmente em problemas relacionados a equações diofantinas e teoria dos grupos.
➤ Computação Gráfica: Em computação gráfica, determinantes são usados para transformações geométricas, como rotações.
➤ Estatística e Probabilidade: Determinantes podem aparecer em contextos estatísticos, por exemplo, ao calcular a matriz de covariância em análise estatística multivariada.
➤ Economia e Ciências Sociais: Modelos econômicos e sistemas de equações nas ciências sociais podem ser analisados usando determinantes.
Em suma, o estudo dos determinantes é indispensável para muitas áreas da Matemática e das ciências, fornecendo ferramentas poderosas para resolver problemas e modelar situações em diversos campos.
Introdução

|
Até aqui, muito se falou sobre o desenvolvimento da teoria dos determinantes. Mas, afinal, o que é determinante?
|
Determinante é uma função matricial que associa a cada matriz quadrada um escalar, ou seja, é uma função que transforma uma matriz quadrada em um número real. O determinante de uma matriz [tex]M[/tex] é denotado por [tex]\det M[/tex] ou simplesmente [tex]|M|[/tex].
Em termos matemáticos, sendo [tex]\mathcal{M}[/tex] o conjunto de todas as matrizes quadradas, temos
[tex]\qquad \begin{align*} \det: \mathcal{M} &\rightarrow \mathbb{R} \\ M &\mapsto \det M \end{align*}[/tex]
Assim, as matrizes abaixo, por serem quadradas, possuem determinantes:
- [tex]A =\begin{bmatrix} 5 \end{bmatrix}[/tex];
- [tex]B=\begin{bmatrix} 1 & 4 \\ -2 & 4\end{bmatrix}[/tex];
- [tex]C=\begin{bmatrix} 1 & 4 & 0 \\ -2 & 4 & 3 \\ 2 & 1 & 1\end{bmatrix}[/tex];
- [tex]D=\begin{bmatrix} 1 & 1 & 0 & 1\\ -1& 2 & -2 & 0\\ 2 & 1 & 1 & 1\\ -2 & 1 & 0 & -1\end{bmatrix}[/tex].
Podemos representar o determinante da matriz [tex]C[/tex] por [tex]\det C[/tex], [tex]|C|[/tex] ou ainda [tex]\begin{vmatrix} 1 & 4 & 0 \\ -2 & 4 & 3 \\ 2 & 1 & 1\end{vmatrix}[/tex].
Como calcular o determinante?
O método utilizado para encontrar o determinante de uma matriz nem sempre é o mesmo. Assim, apresentaremos algumas definições formais de determinante de matrizes de ordens [tex]n = 1[/tex], [tex]n=2[/tex] e [tex]n=3[/tex].
Determinante de uma matriz de ordem [tex]n=1[/tex]
Se [tex]M[/tex] é uma matriz de ordem [tex]n =1[/tex], então [tex]\det M[/tex] é o único elemento de [tex]M[/tex]. Ou seja, se [tex]M =\begin{bmatrix} a_{11}\end{bmatrix}[/tex], então [tex]\det M = a_{11}[/tex].
Exemplos:
1) Se [tex]M =\begin{bmatrix} 5\end{bmatrix}[/tex], então [tex]\det M = 5[/tex];
2) Se [tex]N =\begin{bmatrix} -2\end{bmatrix}[/tex], então [tex]\det N = -2[/tex].
Determinante de uma matriz de ordem [tex]n=2[/tex]
Sendo [tex]M=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix}[/tex] uma matriz de ordem [tex]n =2[/tex], o [tex]\det M[/tex] é o produto de [tex]a_{11}[/tex] e [tex]a_{22}[/tex] menos o produto de [tex]a_{12}[/tex] e [tex]a_{21}[/tex]. Ou seja, [tex]\det M = a_{11}a_{22}-a_{12}a_{21}[/tex].
Exemplos:
1) Se [tex]M=\begin{bmatrix} 1 & -2 \\ 4 & 3\end{bmatrix}[/tex], então [tex]\det M = 1\cdot 3-(-2)\cdot 4=11[/tex];
2) Se [tex]N=\begin{bmatrix} -1 & 0 \\ 2 & 7\end{bmatrix}[/tex], então [tex]\det N = -1\cdot 7-0\cdot 2=-7[/tex].
Determinante de uma matriz de ordem [tex]n=3[/tex]
Se [tex]M[/tex] é uma matriz de ordem [tex]n =3[/tex], digamos [tex]M=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{bmatrix}[/tex], definimos o determinante de [tex]M[/tex] por [tex]\qquad \det M = a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32} -a_{13}\cdot a_{22}\cdot a_{31} – a_{11}\cdot a_{23}\cdot a_{32} -a_{12}\cdot a_{21}\cdot a_{33}.[/tex]
Exemplos:
1) Se [tex]M=\begin{bmatrix} 1 & -2 & 3 \\ 2 & 1 & -1\\ -2 & -1 & 2\end{bmatrix}[/tex], então
[tex]\qquad \begin{align}\det M &= 1\cdot 1\cdot 2+(-2)\cdot (-1)\cdot (-2)+3\cdot 2\cdot (-1) -3\cdot 1\cdot (-2) – 1\cdot (-1)\cdot (-1) -(-2)\cdot 2\cdot 2\\
\det M &= 2-4-6+6-1+8\\
\det M &= 5;\end{align}[/tex]
2) Se [tex]N=\begin{bmatrix} 1 & 2 & 3 \\ 0 & -1 & 1\\ 0 & -2 & 1\end{bmatrix}[/tex], então
[tex]\qquad \begin{align}\det N &= 1\cdot (-1)\cdot 1+ 2\cdot 1\cdot 0+3\cdot 0\cdot (-2) -3\cdot (-1)\cdot 0 – 1\cdot 1\cdot (-2) -2\cdot 0\cdot 1\\
\det N &= -1+0+0+0+2+0\\
\det N &= 1.\end{align}[/tex]
Você deve ter achado um tanto complicada a definição de determinante para o caso de matrizes de ordem [tex]n=3[/tex], não é mesmo? Por consequência, vamos apresentar uma maneira de memorizar com mais facilidade a expressão do determinante [tex]\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{vmatrix}[/tex]:
- Repita, do lado direito da matriz [tex]M[/tex], suas duas primeiras colunas, conforme esquema abaixo.
[tex]\qquad \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{vmatrix}
\begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32} \\
\end{array}[/tex] - Os termos precedidos pelo sinal [tex]+[/tex], na definição apresentada, são obtidos multiplicando-se os elementos situados segundo as setas que estão na mesma direção da diagonal principal. Observe:
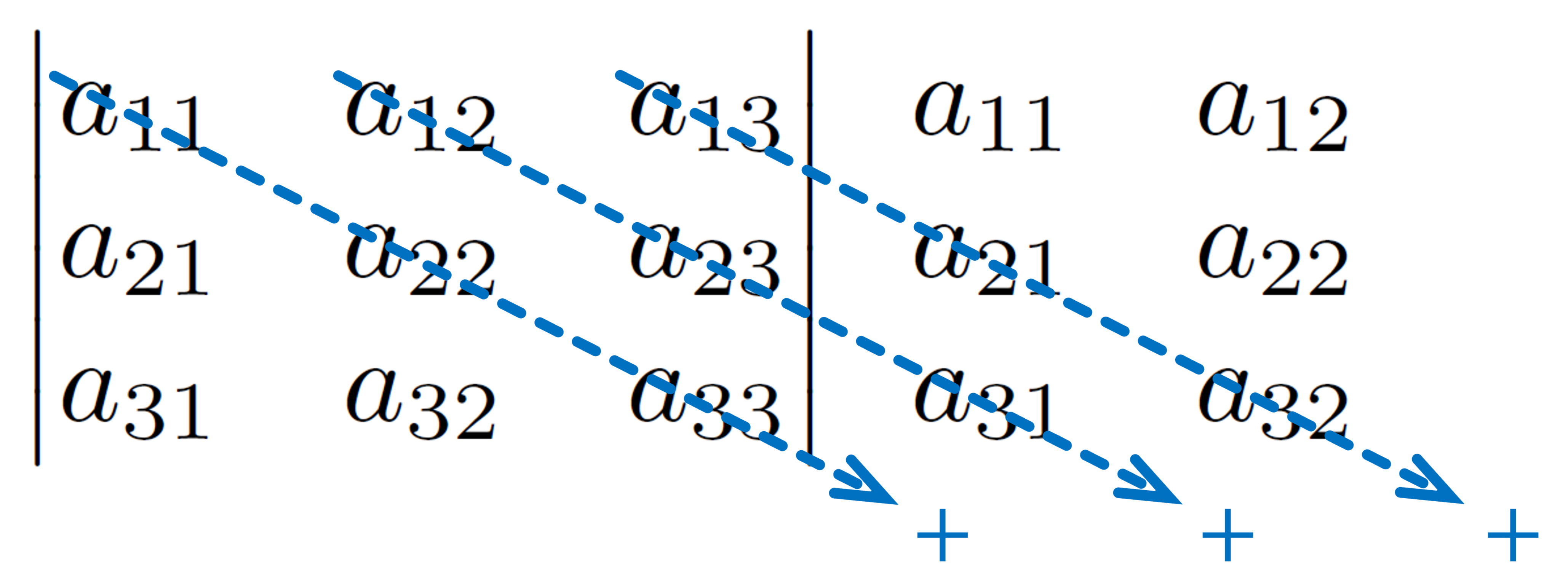
- Os termos precedidos pelo sinal [tex]-[/tex], na definição apresentada, são obtidos multiplicando-se os elementos situados segundo as setas que estão na mesma direção da diagonal secundária. Veja:
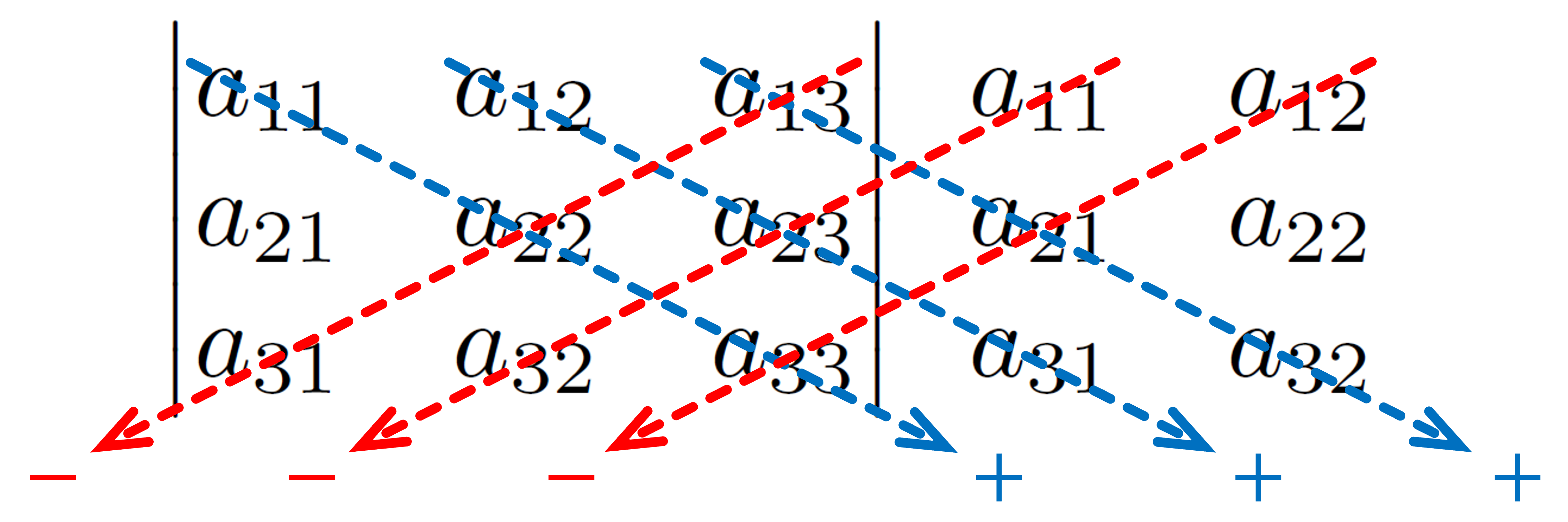
Dessa forma,
[tex]\qquad \begin{align}\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{vmatrix} = \;\;&\textcolor{blue}{a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32}} \\
&\textcolor{red}{-a_{13}\cdot a_{22}\cdot a_{31} – a_{11}\cdot a_{23}\cdot a_{32} -a_{12}\cdot a_{21}\cdot a_{33}.}\end{align}[/tex]
Exemplo: Encontre o determinante da matriz [tex]A=\begin{bmatrix} -1 & 0 & 2 \\ 3& 1& 1\\ -2& 1& 3\end{bmatrix}[/tex].
Solução: Usando o esquema visto acima, temos
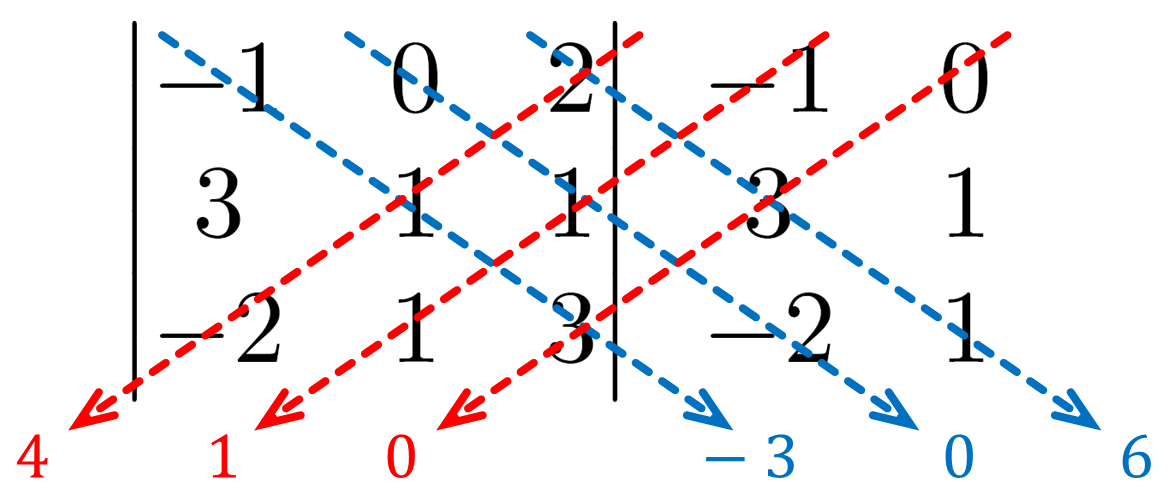
Logo, [tex]\det A = -3+0+6+4+1+0 = 8[/tex].
Esse esquema de memorização para calcular o determinante de uma matriz de ordem 3 é chamado de Regra de Sarrus, que recebe este nome em homenagem ao matemático francês Pierre Frédéric Sarrus (1798 – 1861). Sarrus foi reconhecido por seus trabalhos em várias áreas da Matemática, incluindo a teoria dos determinantes, na qual a regra que leva seu nome se destaca como uma ferramenta de cálculo valiosa e amplamente utilizada.
Até aqui, já sabemos calcular determinantes de matrizes de ordens 1, 2 e 3, mas e se quiséssemos calcular o determinante de uma matriz de ordem superior, como deveríamos proceder? Bom, a seguir vamos apresentar uma definição formal de determinante, válida para matrizes de ordem [tex]n[/tex] qualquer.
Para tanto, vamos precisar de algumas definições:
Definição: Seja [tex]M[/tex] uma matriz quadrada de ordem [tex]n\geq 2[/tex]. Definimos menor complementar do elemento [tex]a_{ij}[/tex] (representamos por [tex]D_{ij}[/tex]) como sendo o determinante da matriz de ordem [tex]n-1[/tex] que se obtém eliminando-se a i-ésima linha e a j-ésima coluna da matriz [tex]M[/tex].
Esquematicamente, se [tex]M=(a_{ij})_{n\times n}[/tex], eliminamos a linha [tex]i[/tex] e a coluna [tex]j[/tex], conforme figura abaixo:

E então
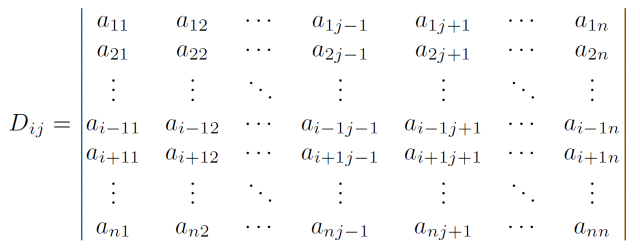
 |
Achou a representação um pouco confusa? 😕 |
Se, por exemplo, [tex]M=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{bmatrix}[/tex], então o menor complementar do elemento [tex]a_{12}[/tex] é o determinante da matriz que se obtém eliminando-se a primeira linha e a segunda coluna da matriz [tex]M[/tex], conforme esquema abaixo.
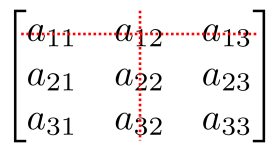
Ou seja, [tex]D_{12} = \begin{vmatrix} a_{21} &a_{23}\\a_{31}& a_{33} \end{vmatrix}.[/tex]
Exemplo: Dada a matriz [tex]M = \begin{bmatrix} 4 &-6& -2\\-1& 3 &-4\\4 &3& 1 \end{bmatrix}[/tex]:
- o menor complementar do elemento [tex]a_{11}[/tex] é [tex]D_{11} = \begin{vmatrix} 3 &-4\\3& 1 \end{vmatrix} = 3+12 = 15[/tex];
- o menor complementar do elemento [tex]a_{23}[/tex] é [tex]D_{23} = \begin{vmatrix} 4 &-6\\4& 3 \end{vmatrix} = 12+24 = 36[/tex].
Definição: Seja [tex]M[/tex] uma matriz quadrada de ordem [tex]n\geq 2[/tex]. Definimos complemento algébrico do elemento [tex]a_{ij}[/tex] (ou simplesmente cofator de [tex]a_{ij}[/tex]), e indicamos por [tex]C_{ij}[/tex], o número [tex](-1)^{i+j}\cdot D_{ij}[/tex].
No que diz respeito ao último exemplo apresentado acima, temos que:
- o cofator de [tex]a_{11}[/tex] é dado por [tex]C_{11} = (-1)^{1+1}\cdot D_{11} = 15[/tex];
- o cofator de [tex]a_{23}[/tex] é dado por [tex]C_{23} = (-1)^{2+3}\cdot D_{23} = (-1)\cdot 36 = -36[/tex].
Caso geral
Definição
Seja [tex]M = (a_{ij})_{n\times n}[/tex] uma matriz de ordem [tex]n[/tex]. Definimos o determinante da matriz [tex]M[/tex] (indicamos por [tex]\det M[/tex]) da seguinte forma:
1) se [tex]n=1[/tex], ou seja, se [tex]M=\begin{bmatrix} a_{11} \end{bmatrix}[/tex], então [tex]\det M =\begin{vmatrix} a_{11}\end{vmatrix} = a_{11}[/tex];
2) se [tex]n\geq 2[/tex], ou seja, se [tex]M = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}[/tex], então [tex]\det M[/tex] é a soma dos produtos dos elementos da 1ª coluna pelos respectivos cofatores.
Ou seja,
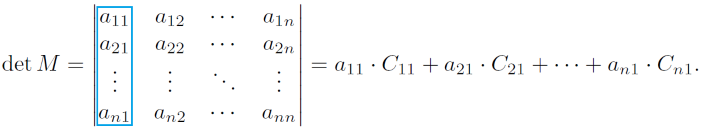
Exemplo: Encontre o determinante da matriz [tex]M=\begin{bmatrix}
3 & -5 & 2 & 7 \\
-1 & 6 & -4 & 9 \\
8 & -2 & 0 & 4 \\
-3 & 1 & -6 & 5
\end{bmatrix}[/tex].
Solução: Pela definição apresentada acima, temos
[tex]\qquad \det M = 3\cdot C_{11}-1\cdot C_{21}+8\cdot C_{31}-3\cdot C_{41}[/tex].
Nos resta calcular o cofator de cada um dos elementos da primeira coluna:
- [tex]C_{11} = (-1)^{1+1}\cdot D_{11} = D_{11} = \begin{vmatrix}
6 & -4 & 9 \\
-2 & 0 & 4 \\
1 & -6 & 5
\end{vmatrix} = 0-16+108+144 -40-0= 196;[/tex] - [tex]C_{21} = (-1)^{2+1}\cdot D_{21} = -D_{21} = -\begin{vmatrix}
-5& 2 & 7 \\
-2 & 0 & 4 \\
1 & -6 & 5
\end{vmatrix} = -(0+8+84-120+20-0)= 8;[/tex] - [tex]C_{31} = (-1)^{3+1}\cdot D_{31} = D_{31} = \begin{vmatrix}
-5 & 2 & 7 \\
6 & -4 & 9 \\
1 & -6 & 5
\end{vmatrix} = 100+18-252+28-60-270= -436;[/tex] - [tex]C_{41} = (-1)^{4+1}\cdot D_{41} = -D_{41} = -\begin{vmatrix}
-5 & 2 & 7 \\
6 & -4 & 9 \\
-2 & 0 & 4
\end{vmatrix} = -(80-36+0-56-48+0)= 60.[/tex]
Portanto,
[tex]\qquad \det M = 3\cdot 196-1\cdot 8+8\cdot (-436)-3\cdot 60[/tex]
[tex]\qquad \det M =−3088[/tex].
Agora, propomos abaixo um exercício para calcular o determinante de uma matriz de ordem [tex]n=5[/tex].
Exercício: Determine o determinante da matriz [tex]M = \begin{bmatrix}
12 & 9 & -13 & -2 & 6 \\
18 & 0 & 0 & 0 & 0 \\
-5 & 8 & 11 & -2 & 14 \\
-1 & 2 & -3 & 1 & 7 \\
9 & 0 & 1 & 0 & 0 \\
\end{bmatrix}[/tex].
 |
Você pode ter se sentido desanimado ao deparar-se com o exercício proposto, não é mesmo? |
|
Vou demorar um século para resolver o exercício! |
 |
 |
Calma! Nem tudo é o que parece ser. Vamos apresentar um resultado muito importante que pode ajudá-lo bastante. |
Teorema de Laplace
O determinante de uma matriz [tex]M[/tex], de ordem [tex]n\geq 2[/tex], é a soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) pelos respectivos cofatores.
Assim, se [tex]M = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1j}& \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2j}& \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots& \ddots & \vdots\\
a_{i1} & a_{i2} & \cdots & a_{ij}& \cdots & a_{in}\\
\vdots & \vdots & \ddots & \vdots& \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nj}& \cdots & a_{nn}
\end{bmatrix}[/tex], então para qualquer [tex]1\leq i\leq n[/tex],
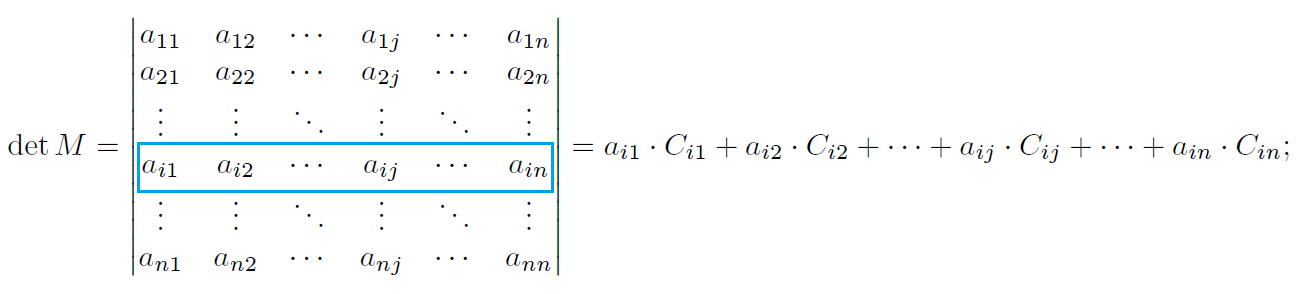
e, para qualquer [tex]1\leq j\leq n[/tex],
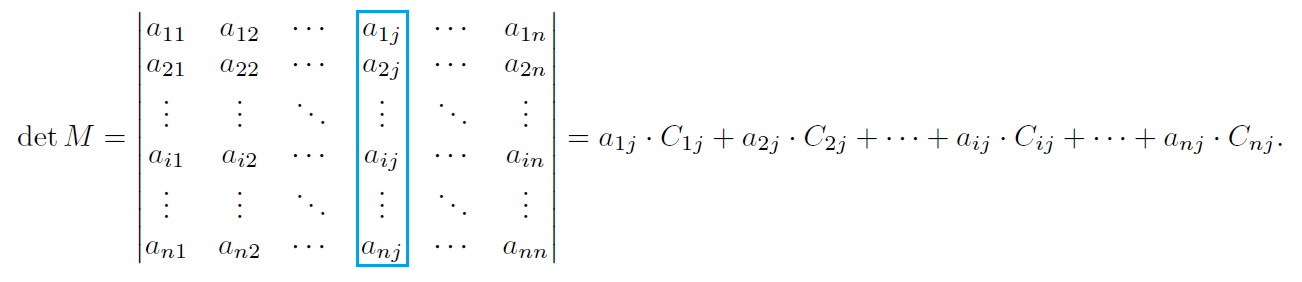
Por enquanto, vamos nos abster de demonstrar a validade desse resultado, já que sua compreensão requer um conhecimento mais aprofundado que foge ao escopo deste estudo.
Exemplo: Calcule o determinante da matriz [tex]M=\begin{bmatrix}
2 & 4 & 1 & 3 \\
-1 & 0 & 2 & 5 \\
3 & 1 & -2 & 0 \\
0 & 2 & 1 & -3 \\
\end{bmatrix}[/tex].
Solução: Escolhendo a terceira linha da matriz e aplicando o teorema de Laplace, temos
[tex]\begin{align}\det M &= 3\cdot(-1)^{3+1}\cdot\begin{vmatrix}
4 & 1 & 3 \\
0 & 2 & 5 \\
2 & 1 & -3 \\
\end{vmatrix} +1\cdot(-1)^{3+2}\cdot \begin{vmatrix}
2 & 1 & 3 \\
-1 & 2 & 5 \\
0 & 1 & -3 \\
\end{vmatrix}-2\cdot(-1)^{3+3}\cdot \begin{vmatrix}
2 & 4 & 3 \\
-1 & 0 & 5 \\
0 & 2 & -3 \\
\end{vmatrix}+0\cdot(-1)^{3+4}\cdot \begin{vmatrix}
2 & 4 & 1 \\
-1 & 0 & 2 \\
0 & 2 & 1 \\
\end{vmatrix}\\
&= 3\cdot\begin{vmatrix}
4 & 1 & 3 \\
0 & 2 & 5 \\
2 & 1 & -3 \\
\end{vmatrix} -1\cdot \begin{vmatrix}
2 & 1 & 3 \\
-1 & 2 & 5 \\
0 & 1 & -3 \\
\end{vmatrix}-2\cdot \begin{vmatrix}
2 & 4 & 3 \\
-1 & 0 & 5 \\
0 & 2 & -3 \\
\end{vmatrix}-0\cdot \begin{vmatrix}
2 & 4 & 1 \\
-1 & 0 & 2 \\
0 & 2 & 1 \\
\end{vmatrix}\\
&= 3\cdot(-46) -1\cdot (-28)-2(-38)-0\cdot(-6)\\
&=-34.\end{align}[/tex]
Bom, agora iremos resolver o exercício proposto anteriormente.
Exercício: Determine o determinante da matriz [tex]M = \begin{bmatrix}
12 & 9 & -13 & -2 & 6 \\
18 & 0 & 0 & 0 & 0 \\
-5 & 8 & 11 & -2 & 14 \\
-1 & 2 & -3 & 1 & 7 \\
9 & 0 & 1 & 0 & 0 \\
\end{bmatrix}[/tex].
Solução: Obviamente procuramos uma maneira mais simples de resolver o problema. Dessa forma, a fim de simplificarmos os cálculos, é ideal que escolhamos a linha ou a coluna que tenha a maior quantidade possível de elementos iguais a [tex]0[/tex] para aplicarmos o teorema de Laplace. Neste caso, como a matriz é dada por
[tex]\qquad M = \begin{bmatrix}
12 & 9 & -13 & -2 & 6 \\
18 & 0 & 0 & 0 & 0 \\
-5 & 8 & 11 & -2 & 14 \\
-1 & 2 & -3 & 1 & 7 \\
9 & 0 & 1 & 0 & 0 \\
\end{bmatrix}[/tex],
escolhemos aplicar o teorema de Laplace na 2ª linha, pois esta tem quatro elementos iguais a [tex]0[/tex]. Assim,
[tex]\qquad \det M = 18\cdot C_{21}+0\cdot C_{22}+0\cdot C_{23}+0\cdot C_{24}+0\cdot C_{25}[/tex]
[tex]\qquad \det M = 18\cdot C_{21}[/tex]
[tex]\qquad \det M = 18\cdot (-1)^{2+1}\cdot D_{21}[/tex]
[tex]\qquad \det M = -18\cdot D_{21}[/tex].
Repare que
[tex]\qquad D_{21} = \begin{vmatrix}
9 & -13 & -2 & 6 \\
8 & 11 & -2 & 14 \\
2 & -3 & 1 & 7 \\
0 & 1 & 0 & 0 \\
\end{vmatrix}.[/tex]
Novamente, podemos aplicar o teorema de Laplace, desta vez, na 4ª linha, pois dentre todas as linhas e colunas esta é a que possui a maior quantidade de elementos iguais a [tex]0[/tex]. Portanto,
[tex]\qquad D_{21} = 0\cdot C_{41}+1\cdot C_{42}+0\cdot C_{43}+0\cdot C_{44}[/tex]
[tex]\qquad D_{21} = 1\cdot C_{42}[/tex]
[tex]\qquad D_{21} = 1\cdot (-1)^{4+2}D_{42}[/tex]
[tex]\qquad D_{21} = D_{42}[/tex].
Observe que [tex]D_{42}[/tex] acima corresponde ao menor complementar do elemento [tex]a_{42}[/tex] da matriz [tex]D_{21}[/tex]. Ou seja,
[tex]\qquad D_{21} = D_{42} = \begin{vmatrix}
9 & -2 & 6 \\
8 & -2 & 14 \\
2 & 1 & 7 \\
\end{vmatrix} = -124[/tex].
Logo,
[tex]\qquad \det M = -18\cdot D_{21}[/tex]
[tex]\qquad \det M = -18\cdot (-124) [/tex]
[tex]\qquad \boxed{\det M =2232}[/tex].
 |
Nem foi tão complicado, não é mesmo? |
Até aqui, já temos conhecimento suficiente para calcularmos o determinante de uma matriz de ordem [tex]n[/tex] qualquer, podendo, inclusive, às vezes, termos sucesso mais rápido quando utilizamos o teorema de Laplace, uma vez que este pode ser uma mão na roda quando se tem, na matriz em questão, elementos iguais a zero, como vimos anteriormente. No entanto, no estudo de determinantes podemos destacar mais algumas ferramentas que podem ser usadas para facilitar o cálculo de determinantes de matrizes. A próxima seção trata de tais ferramentas e, em algumas delas, omitiremos a demonstração da validade, já que sua compreensão requer conhecimento aprofundado de um tema que ainda não vimos.
Como já sabemos o que é o determinante de uma matriz e já aprendemos a calculá-lo, vamos aprofundar um pouco a nossa discussão.
Para isso, vamos apresentar três novas Salas: duas com assuntos específicos e uma terceira com problemas.
➤ Sala 2: Regra de Chió.
➤ Sala 3: Problemas.
Recomendamos fortemente que vocês continuem a leitura seguindo a ordem na qual essas Salas estão anunciadas.
Vamos lá?
| Sala 1 | Sala 2 | Sala 3 |
Equipe COM – OBMEP
Fevereiro de 2025
[1] Asymptotic Behaviour of Random Vandermonde Matrices with Entries on the Unit Circle (Último acesso em 29/06/24)
[2] MacTutor – Matrices and determinants(Último acesso em 29/06/24)
[3] Wikipédia – Determinante(Último acesso em 29/06/24)
[4] IEZZI, Gelson. HAZZAN, Samuel. Fundamentos de matemática elementar, 4: Sequências, Matrizes, Determinantes e Sistemas. 10. ed. São Paulo: Atual, 2013.
