Trigonometria do
triângulo retângulo
I – Apresentação do Tema
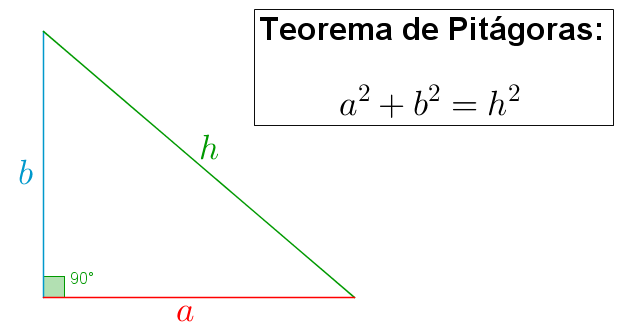
Ao falarmos sobre triângulos retângulos, a primeira propriedade que vem à cabeça de muitos de vocês, certamente, é o Teorema de Pitágoras. Mas, apesar de sua beleza e aplicabilidade, o Teorema de Pitágoras não é a única propriedade importante dos triângulos retângulos.
Nesta Sala de Estudos, vamos explorar os triângulos retângulos utilizando ferramentas da Geometria como, por exemplo, semelhança, para obtermos várias propriedades interessantes e largamente utilizadas em medições indiretas. E, diferentemente do Teorema de Pitágoras, que utiliza apenas as medidas dos lados dos triângulos retângulos, aqui utilizaremos também as medidas dos dois ângulos agudos desses triângulos, já que o início das nossas discussões será estabelecer, de alguma forma, relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo.
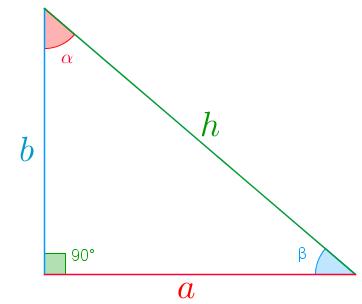
O ramo da matemática que estuda relações entre ângulos e lados de um triângulo é a Trigonometria.
A palavra trigonometria vem do grego – τριγωνομετρία – que é a composição das palavras gregas τρίγωνον (trigonon: triângulo) e μέτρον (metron: medida). A primeira dessas, por sua vez, é composta das palavras τρεῖς, τρία (tris, tría: três) e γωνία (gonia: ângulo).
Assim, utilizaremos os significados dos três radicais gregos que formam a palavra Trigonometria
tri (três) + gonos (ângulos) + metron (medidas)
para apresentar o objetivo central desta Sala de Estudos:
estudar medições em triângulos.
A Trigonometria atua direta ou indiretamente em vários ramos da Matemática que requerem medidas de precisão e tem numerosas aplicações na Astronomia, na Topografia, no estudo de imagens digitais, em sistemas de navegação por satélites, e, de maneira geral, na determinação de ângulos e de distâncias inacessíveis. Nesta sala, apresentaremos algumas das aplicações geométricas da Trigonometria.
E se vocês estão habituados a ver a palavra trigonometria em tópicos do ensino médio, não se preocupem: para entender o que vai ser tratado aqui, vocês só precisam saber um pouco sobre triângulos!
II – Um pouco de História
Há mais de 3000 anos, os egípcios e os babilônicos assistiram ao início do desenvolvimento da Trigonometria, que surgiu, principalmente, devido a problemas da Astronomia, Agrimensura, Construção e Navegação. Medidas na agrimensura, medidas para a construção de pirâmides, previsão de rotas e posições de corpos celestes, melhoria na exatidão de rotas de navegação e no cálculo do tempo foram situações específicas nas quais são encontrados os primeiros indícios de rudimentos da Trigonometria.
No papiro Rhind, por exemplo, são encontrados problemas envolvendo trigonometria. O papiro Rhind, ou Ahmes, mede 5,5 m de comprimento por 0,32 m de largura e data de, aproximadamente, 1650 a.C. É um texto matemático escrito na forma de manual prático e contém 85 problemas copiados em escrita hierática, pelo escriba Ahmes, de um trabalho mais antigo.
Estudiosos apontam que na tábua cuneiforme Plimpton 322 há indícios de elementos de trigonometria. A Plimpton 322 é considerada a mais notável dentre todas as tabletas babilônicas já encontradas. É uma tábua de argila, parcialmente quebrada, medindo cerca de 12,7 cm de largura, 8,8 cm de altura e 2 cm de espessura, que foi recuperada no deserto do Iraque. Estima-se que o texto foi escrito entre 1900 e 1600 a.C.
 Uma parte do papiro Rhind – Museu Britânico, Londres. |
 Plimpton 322 – Columbia University. |
Ainda como parte da Astronomia, o estudo da Trigonometria se difundiu pela Grécia, Índia e Arábia. Os gregos antigos fizeram um estudo sistemático das relações entre ângulos – ou arcos – numa circunferência e os comprimentos de suas cordas.

Hiparco de Nicéia (180 – 125 a.C)
Particularmente o astrônomo, construtor, cartógrafo e matemático grego Hiparco de Nicéia, que viveu entre os anos 180 e 125 a.C. e que ganhou o direito de ser chamado de o “Pai da Trigonometria”, construiu uma tabela com comprimentos de cordas que é considerada a primeira tabela trigonométrica. Com a ajuda dessa tabela ele podia relacionar facilmente os lados e os ângulos de qualquer triângulo do plano. Mais do que isso, fortemente influenciado pela matemática babilônica, Hiparco acreditava que a melhor base numérica para contagem era a 60. Dessa forma, introduziu na Grécia a divisão da circunferência em [tex]360[/tex] partes iguais, atribuiu o nome “arco de 1 grau” a cada parte em que a circunferência ficou dividida e dividiu cada arco de 1 grau em 60 partes obtendo, assim, o “arco de 1 minuto”. Infelizmente, os doze livros que continham a trigonometria de Hiparco, assim como o restante da sua obra, se perderam com o tempo…

Cláudio Ptolomeu (90 – 168)
No entanto, o conhecimento produzido por Hiparco foi preservado e ampliado brilhantemente por Cláudio Ptolomeu (90 – 168): extraordinário astrônomo, geógrafo, físico e matemático da Universidade de Alexandria que também estudou os astros com a ajuda da trigonometria. É dele o mais influente e significativo compêndio de Astronomia da Antiguidade: Syntaxis mathematica. Escrita em 13 volumes, essa obra ficou conhecida como Almagesto, que significa “o maior”, em árabe, já que os tradutores árabes a consideravam a maior obra sobre Astronomia existente na época. A trigonometria de Ptolomeu aparece nos capítulos dez e onze do primeiro livro do Almagesto, como pré-requisito para o restante da obra. O Almagesto foi a mais importante fonte de consulta para os astrônomos até o século VIII, época na qual o mundo começa a conhecer a matemática hindu.
Com a matemática hindu apareceram razões trigonométricas, como as que trabalharemos nesta Sala, e os métodos de se obter tabelas trigonométricas foram aperfeiçoados. Mais do que isso, a Índia revolucionou a Trigonometria com um conjunto de textos denominados Siddhanta, que significa sistemas de Astronomia. Apesar das poucas explicações e de nenhuma prova, o Siddhanta segue um caminho diferente do caminho do Almagesto de Ptolomeu e substitui a relação entre “as cordas de um círculo e os ângulos centrais correspondentes” pela relação entre “a metade das cordas de um círculo e a metade dos ângulos centrais correspondentes”, relação essa chamada por eles de jiva. Surge aí a “Trigonometria no triângulo retângulo”.
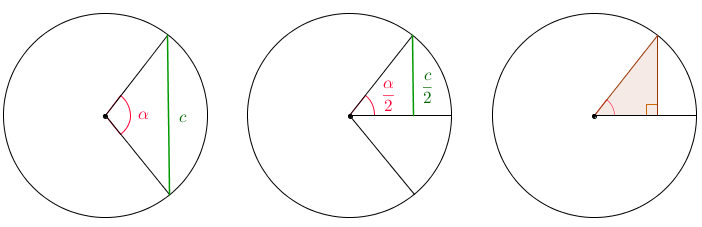
O conflito entre a Trigonometria do Almajesto e a Trigonometria hindu termina quando o matemático árabe al-Battani (850 – 929) adota a Trigonometria hindu, introduzindo uma inovação preciosa para a matemática: o círculo de raio unitário.
Da Arábia, a Trigonometria alcançou a Europa, onde se separa da Astronomia para se tornar um ramo independente da Matemática. Nesse novo caminho, a Trigonometria ganha um tratamento analítico com o matemático francês François Viète (1540-1603), que também desenvolveu métodos para determinar triângulos planos e esféricos. No início do século XVII, o matemático escocês John Napier (1550-1617) fez, também, contribuições para a trigonometria esférica.
No século XVIII, como não poderia deixar de ser, a trigonometria recebeu contribuições importantes do matemático inglês Isaac Newton (1643-1727) e do matemático suíço Leonhard Euler (1707-1783). Particularmente, Euler fundou a trigonometria moderna, introduziu a notação atual das funções trigonométricas e estabeleceu a relação da função exponencial com as funções trigonométricas, o que permitiu inseri-las no campo dos números complexos. Com Euler, a trigonometria toma a sua forma atual!
|
|
 |
 |
 |
| François Viète | John Napier | Isaac Newton | Leonhard Euler |
III – Razões especiais
Vamos iniciar este tópico estabelecendo três razões entre números reais: essas razões aparecem de maneira natural quando lidamos com triângulos retângulos semelhantes e são conhecidas como razões trigonométricas.
Para acompanhar sem problemas a nossa discussão, é necessário que vocês saibam o que é um triângulo retângulo e o que são triângulos semelhantes.
Se vocês não se lembram desses dois conceitos matemáticos, não faz mal: para um reencontro com os triângulos retângulos cliquem aqui e, para relembrar um pouco sobre triângulos semelhantes, cliquem aqui.
Antes de prosseguir, informamos que:
(1) As notações para segmentos de reta e seus comprimentos definidas nessas duas salas de ajuda, assim como a identificação entre segmentos e suas medidas, serão também utilizadas nesta Sala.
(2) Para simplificar notação, sempre que necessário, identificaremos um ângulo por sua medida. Assim, se um ângulo de vértice [tex]A[/tex] tem medida [tex]\alpha[/tex], então poderemos nos referir a ele como [tex]\widehat{A}[/tex] ou ângulo [tex]\alpha[/tex], desde que não haja comprometimento de interpretação.
E aí, prontos?
Considere uma família de triângulos retângulos [tex]A_1C_1B_1, \, \, A_2C_2B_2, \, \, A_3C_3B_3, \, \, … , \, \, A_nC_nB_n, \, \, …[/tex] de modo que cada triângulo [tex]A_iC_iB_i[/tex] tenha um dos ângulos com medida [tex]\theta[/tex], [tex]0^{\circ} \lt \theta \lt 90^{\circ}[/tex].
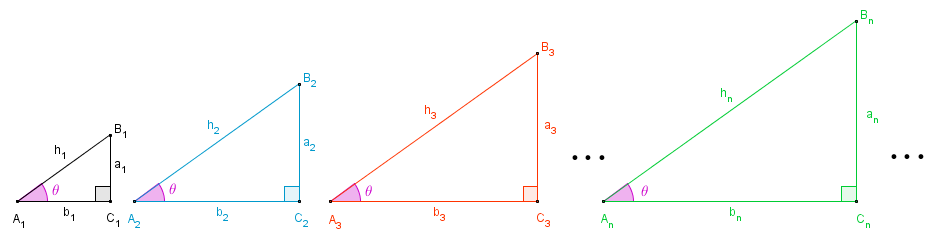
Como, dois a dois, esses triângulos têm dois ângulos com a mesma medida, respectivamente [tex]\theta[/tex] e [tex]90^{\circ}[/tex], então todos os triângulos da família são semelhantes e, consequentemente:
● [tex]\dfrac{a_1}{b_1}= \dfrac{a_2}{b_2}=\dfrac{a_3}{b_3}=\cdots =\dfrac{a_n}{b_n}=\cdots [/tex]
● [tex]\dfrac{a_1}{h_1}= \dfrac{a_2}{h_2}=\dfrac{a_3}{h_3}=\cdots =\dfrac{a_n}{h_n}=\cdots [/tex]
● [tex]\dfrac{b_1}{h_1}= \dfrac{b_2}{h_2}=\dfrac{b_3}{h_3}=\cdots =\dfrac{b_n}{h_n}=\cdots [/tex]
Se vocês quiserem comprovar essas três afirmações para famílias particulares de triângulos retângulos semelhantes, vocês podem utilizar o applet que disponibilizaremos abaixo: é só clicar no botão.
Vamos passar a limpo propriedades que podem ser visualizadas e investigadas com o applet, explicitando alguns resultados matemáticos necessários para realizarmos as discussões desta sala.
Uma observação essencial é que, fixado um ângulo agudo de medida [tex]\theta[/tex], em graus, para todo triângulo retângulo que tenha um de seus ângulos agudos com medida [tex]\theta[/tex], as razões
[tex] \, \dfrac{cateto \, oposto \, a \, \theta}{cateto \, adjacente \, a \, \theta} \, \quad[/tex] [tex]\quad\dfrac{cateto \, oposto \, a \, \theta}{hipotenusa} \, \quad[/tex] [tex]\quad\, \dfrac{cateto \, adjacente \, a \, \theta}{hipotenusa} \, [/tex]
são sempre as mesmas.
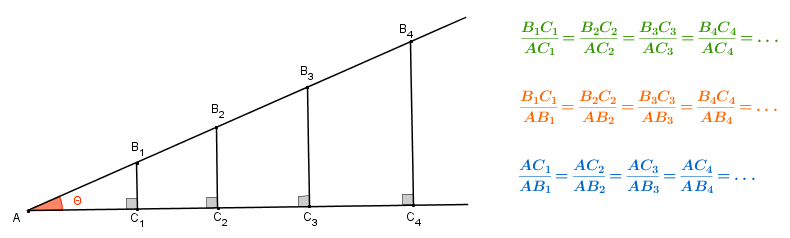
Assim, essas razões não dependem dos comprimentos dos lados dos triângulos retângulos considerados:
elas são determinadas pelo ângulo de medida [tex]\theta[/tex] desses triângulos.
Daremos, então, nomes especiais a essas razões, explicitando a dependência entre elas e o ângulo de medida [tex]\theta[/tex]:
● a constante definida pelas razões entre os comprimentos dos catetos opostos e dos catetos adjacentes dos triângulos retângulos semelhantes será denominada “tangente de [tex]\theta[/tex]” e denotada por [tex]tg \, \theta[/tex]:
[tex]\qquad\qquad tg \, \theta= \frac{B_1C_1}{AC_1} =\frac{B_2C_2}{AC_2} = \frac{B_3C_3}{AC_3} = \frac{B_4C_4}{AC_4} =\dots [/tex];
● a constante definida pelas razões entre os comprimentos dos catetos opostos e das hipotenusas dos triângulos retângulos semelhantes será denominada “seno de [tex]\theta[/tex]” e denotada por [tex] \, sen \, \theta[/tex]:
[tex]\qquad\qquad sen \, \theta= \frac{B_1C_1}{AB_1} = \frac{B_2C_2}{AB_2} = \frac{B_3C_3}{AB_3} = \frac{B_4C_4}{AB_4} =\dots [/tex];
● a constante definida pelas razões entre os comprimentos dos catetos adjacentes e das hipotenusas dos triângulos retângulos semelhantes será denominada “cosseno de [tex]\theta[/tex]” e denotada por [tex]cos \, \theta[/tex]:
[tex]\qquad\qquad cos \, \theta= \frac{AC_1}{AB_1} = \frac{AC_2}{AB_2} = \frac{AC_3}{AB_3} = \frac{AC_4}{AB_4} =\dots [/tex].
Como os valores para o seno, o cosseno e a tangente de ângulos com medidas [tex]\theta[/tex], [tex]0^{\circ} \lt \theta \lt 90^{\circ}[/tex], são constantes, é possível construir tabelas contendo aproximações para tais valores, o que facilita enormemente a manipulação desses dados em aplicações. Essas tabelas são conhecidas como tabelas trigonométricas ou tábuas trigonométricas.
Embora razões trigonométricas possam ser calculadas para ângulos com medidas não inteiras, as tabelas trigonométricas mais simples são as que apresentam as razões trigonométricas definidas para ângulos com medidas inteiras entre [tex]0 \, [/tex] e [tex] \, 90[/tex] graus. Para obter uma tabela dessas, é só clicar nos próximos botões:
● para baixar o arquivo, cliquem no botão da direita;
● para apenas consultar, cliquem no botão da esquerda e, depois da consulta, não se esqueçam de fechar a janela que se abriu.
| Consultar | Baixar o arquivo |
Se vocês nunca utilizaram uma tabela trigonométrica, observem que, a partir do valor de um ângulo, podemos encontrar os valores aproximados dos seus respectivos seno, cosseno e tangente; assim como, a partir do valor de uma razão trigonométrica, conseguimos identificar a medida aproximada do ângulo que a produz. E, por favor, não se assustem com esse monte de números, pois não é preciso decorar o seno, o cosseno e a tangente de todos os possíveis ângulos agudos: tabelas como a que apresentamos podem ser facilmente obtidas em livros ou na Internet. Num primeiro momento, o importante é vocês entenderem direitinho o que é o seno, o cosseno e a tangente de um dado ângulo agudo e terem a certeza de que, se necessário, aproximações para esses valores podem ser obtidas, mesmo sem recorrer a tabelas prontas.
IV – Trigonometria do triângulo retângulo
Vale a pena observarmos, mais uma vez, a praticidade da ideia de que a tangente, o seno e o cosseno de um determinado ângulo agudo de medida [tex]\theta[/tex] podem ser obtidos a partir de um triângulo retângulo conveniente que tenha um de seus ângulos agudos medindo [tex]\theta[/tex]. Isso significa que podemos utilizar tabelas trigonométricas (e calculadoras científicas são tabelas modernas) para obtermos valores de seno, cosseno e tangente de vários ângulos e com isso determinarmos características de triângulos retângulos que apareçam em problemas e até em situações do nosso cotidiano, como a apresentada a seguir.
Um problema inicial
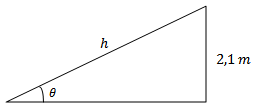
Em uma oficina mecânica, será necessário construir uma rampa para carros, de modo a vencer um desnível de [tex]2,1 \, m[/tex].

Se o ângulo de inclinação deve ter, no máximo, [tex]25^{\circ}[/tex], qual deve ser o comprimento mínimo da rampa? Considerem para a rampa comprimentos representados com uma casa decimal.
Apenas com o que foi até agora exposto, vocês já têm informações mais do que suficientes para resolverem esse probleminha inicial. Mas antes vamos fazer algumas adaptações na linguagem matemática para trabalharmos especificamente com a trigonometria em triângulos retângulos.
A trigonometria do triângulo retângulo nada mais é do que o estudo das propriedades da tangente, do seno e do cosseno de ângulos agudos, a partir de triângulos retângulos escolhidos segundo nossa conveniência. Vamos pôr em prática essa ideia, estabelecendo as próximas definições.
Definições
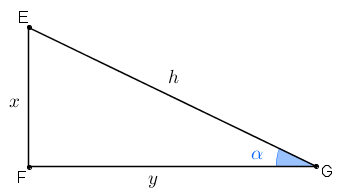
Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a, \, b, \, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
| Chamamos de
● tangente de [tex]\theta[/tex], e denotamos por [tex]tg \, \theta[/tex], a razão entre os comprimentos do cateto oposto e do cateto adjacente a [tex]\theta[/tex]: |
|
|
A facilidade de aplicarmos essas definições nos permite determinar os comprimentos dos catetos de um triângulo retângulo, conhecendo apenas o comprimento de sua hipotenusa e a medida de um de seus ângulos agudos.
Neste caso o comprimento [tex]x \, [/tex] e [tex] \, y[/tex] dos catetos são dados por |
Agora, voltando ao probleminha inicial, por que vocês não tentam solucioná-lo? Vocês poderão conferir a resposta, ou mesmo tentar entender como o problema pode ser resolvido, clicando no botão abaixo.
Embora tenhamos definido as razões trigonométricas geometricamente é bastante razoável a seguinte pergunta:
Senos, cossenos e tangentes têm algum tipo de relação algébrica entre si?
A resposta positiva à essa pergunta nos permitirá trabalhar algebricamente com as razões trigonométricas e isso nos abre a possibilidade de, quem sabe, determinarmos senos, cossenos e tangentes sem fazermos medições, necessariamente. Isso seria bem legal e “econômico”!
Então, vamos investigar?
Atividade: Duas investigações
Nesta atividade vocês deverão procurar relações algébricas entre:
✐ seno, cosseno ou tangente de um mesmo ângulo;
✐ senos, cossenos ou tangentes de ângulos complementares.
Para isso, cliquem no próximo botão.
 |
Apresentaremos a seguir as conclusões que gostaríamos que fossem obtidas a partir da Atividade de Investigação que apresentamos acima. |
Propriedades da trigonometria do triângulo retângulo

1) Relações fundamentais
Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a, \, b, \, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Nessas condições, são válidas as seguintes propriedades:
a) [tex]sen^2\theta + cos^2\theta = 1 \qquad\qquad[/tex]b) [tex]\dfrac{sen \, \theta}{cos \, \theta} = tg \, \theta[/tex].
2) Ângulos complementares
Considerem dois ângulos agudos complementares com medidas [tex]\alpha[/tex] e [tex]\beta[/tex].
Então:
a) [tex] \, \, sen \, \alpha = cos \, \beta \qquad\qquad[/tex]b)[tex] \, tg \, \alpha = \dfrac{1}{tg \, \beta}[/tex].
3) Ângulos com medidas menores do que [tex]45^{\circ}[/tex]
Seja [tex]\theta[/tex] tal que [tex]0^{\circ} \lt \theta \lt 45^{\circ}[/tex].
Então:
a)[tex] \, sen \, 2\theta=2sen\theta \cdot cos\theta\qquad\qquad[/tex]
b) [tex]sen \, \frac{\theta}{2}=\sqrt{\frac{1-cos \, \theta}{2}}[/tex].
4) Ângulos especiais
a) [tex] \, \, sen \, 30^{\circ}=\dfrac{1}{2}\qquad\qquad \, \, \, \, cos \, 30^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad tg \, 30^{\circ}=\dfrac{\sqrt{3}}{3}[/tex] .
b) [tex] \, \, sen \, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] cos \, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] tg \, 45^{\circ}=1[/tex] .
c) [tex] \, \, sen \, 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos \, 60^{\circ}=\dfrac{1}{2}\qquad\qquad[/tex] [tex] \, \, \, \, tg \, 60^{\circ}=\sqrt{3}[/tex] .
Bons estudos!
 |
Com as próximas propriedades, a partir dos senos e dos cossenos de dois ângulos, será possível obtermos o seno da soma, o seno da diferença, o cosseno da soma e o cosseno da diferença dos dois ângulos iniciais. |
Mais propriedades da trigonometria do triângulo retângulo
5) Cosseno da diferença
Sejam [tex]\alpha \, [/tex] e [tex] \, \beta[/tex] tais que [tex]0^{\circ} \lt \, \beta \, \lt \, \alpha \, \lt 90^{\circ}[/tex]. Então [tex] \, \, \boxed{cos \, (\alpha-\beta)=cos \, \alpha\cdot cos \, \beta+sen \, \alpha\cdot sen \, \beta} \, [/tex].
6) Seno da diferença
Sejam [tex]\alpha \, [/tex] e [tex] \, \beta[/tex] tais que [tex]0^{\circ} \lt \, \beta \, \lt \, \alpha \, \lt 90^{\circ}[/tex]. Então [tex] \, \, \boxed{ sen \, (\alpha-\beta)=sen \, \alpha\cdot cos \, \beta-sen \, \beta\cdot cos \, \alpha} \, [/tex].
7) Cosseno da soma
Sejam [tex]\alpha \, [/tex] e [tex] \, \beta[/tex] tais que [tex]0^{\circ} \lt \, \alpha, \, \, \beta, \, \, \alpha+\beta \, \lt 90^{\circ}[/tex]. Então [tex] \, \, \boxed{cos \, (\alpha+\beta)=cos \, \alpha\cdot cos \, \beta-sen \, \alpha\cdot sen \, \beta} \, [/tex].
8) Seno da soma
Sejam [tex]\alpha \, [/tex] e [tex] \, \beta[/tex] tais que [tex]0^{\circ} \lt \, \alpha, \, \, \beta, \, \, \alpha+\beta \, \lt 90^{\circ}[/tex]. Então [tex] \, \, \boxed{sen \, (\alpha+\beta)=sen \, \alpha\cdot cos \, \beta+sen \, \beta\cdot cos \, \alpha} \, [/tex].
 |
Essas quatro últimas propriedades serão trabalhadas na próxima atividade, na forma de uma Oficina. |
Oficina: Somas e diferenças
As propriedades 5, 6, 7 e 8 permitem obter vários senos e cossenos a partir dos senos e cossenos de dois ângulos que cumpram determinadas condições. Assim, elas também podem ser úteis na construção de tabelas!
Para brincar com essas quatro propriedades, é só clicar no próximo botão.
Bom divertimento!
V – Medindo o que não podemos alcançar…
Não é necessário nem pensar em medir a distância entre a Lua e o Sol para verificar que existem situações para as quais os chamados “métodos diretos de medição da distância entre dois pontos” não dão certo, mesmo fazendo uma série de contorcionismos.
Como o próprio nome sugere, a medida de uma distância de modo direto consiste simplesmente na leitura da distância entre dois pontos mediante a utilização de um instrumento de medida: uma régua graduada, uma fita métrica, uma trena. Já nos chamados processos indiretos de medida, uma distância é obtida via cálculos matemáticos que vinculam a “distância a ser calculada” a “outras que são obtidas de modo direto”.
O probleminha inicial ilustra um processo de medição indireta: o dono da oficina mecânica obteve o comprimento da rampa mesmo sem medi-la, aliás, mesmo sem ter a rampa…
O probleminha inicial ilustra também o modo de se resolver muitos dos problemas que envolvem a determinação indireta de distâncias: a partir dos dados, tentamos encontrar um triângulo retângulo de modo que o comprimento da sua hipotenusa ou de um de seus catetos forneça a distância a ser determinada. Fatalmente, a solução desse tipo de problema requer a utilização de razões trigonométricas. Arquitetos, engenheiros e topógrafos se deparam muitas vezes com problemas desse tipo nos projetos que desenvolvem.
Apresentaremos três exemplos clássicos de problemas que envolvem distâncias que precisam ser obtidas por medição indireta não só para que vocês os resolvam, mas, principalmente, para que vocês observem exemplos de medições diretas necessárias para a solução desse tipo de problema. Por falar em medida, informamos que as figuras que ilustram os problemas não estão em escala.
|
|
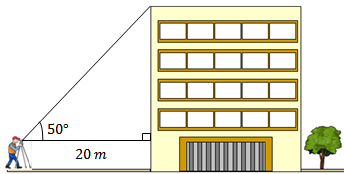
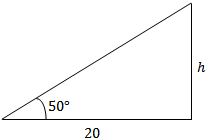
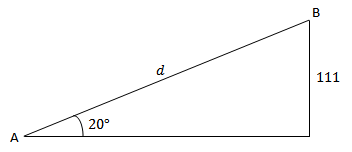
Uma pessoa com [tex]1,75 \, m[/tex] de altura e que se encontra a [tex]20 \, m[/tex] da base de um edifício vê o ponto mais alto dele sob um ângulo de [tex]50^{\circ}[/tex]. Qual a altura aproximada do edifício? |
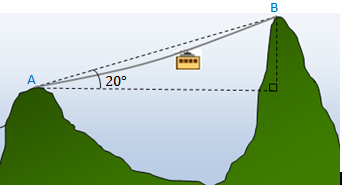 |
A Secretaria de Turismo de uma cidade vai instalar um teleférico ligando os topos de duas montanhas, uma com [tex]872 \, m \, [/tex] e a outra com [tex] \, 761 \, m[/tex] de altura, conforme a figura. Os engenheiros responsáveis pelo projeto mediram o ângulo de vértice [tex]A[/tex] e calcularam que o cabo de aço que sustentará o teleférico tem curvatura e, por isso, seu comprimento é [tex]7\%[/tex] maior que a medida do segmento de reta [tex]AB.[/tex] Assim, calculem o comprimento do cabo. |
|
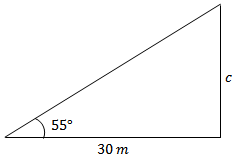
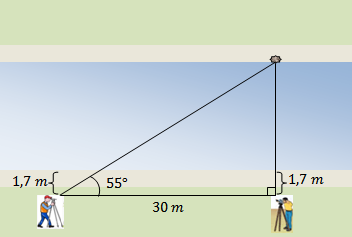
Dois engenheiros estão de um mesmo lado de um rio, separados por [tex]30 \, m[/tex] um do outro. Cada um deles, em sua respectiva posição, observa uma pedra que está na margem do outro lado, segundo um ângulo específico, conforme mostra a figura. Supondo que ambos estão afastados da margem de uma distância de [tex]1,7 \, m[/tex] e que as duas margens do rio são paralelas, qual é a largura do rio? (Desconsiderar a diferença de altura entre os observadores e a pedra.) |
Com um pouquinho de treino, vocês conseguirão resolver rapidamente problemas bem bacanas, utilizando a trigonometria do triângulo retângulo. Vamos deixar alguns para vocês tentarem resolver. Mas, antes, vale observar que, em algumas situações, o triângulo retângulo a ser utilizado pode estar bem escondidinho…
Aí vão os problemas…
 |
Que tal praticar um pouco do que foi aqui apresentado?
|
Equipe COM – OBMEP
Julho de 2016.
➨ iconesbr (Último acesso em 20/06/20)
➨ IMATICA – Papiro Rhind (Último acesso em 20/06/20)
➨ MacTutor – Arquivo História da Matemática (Último acesso em 20/06/20)
➨ The Babylonian tablet Plimpton 322 (Último acesso em 20/06/20)
➨ YouTube (Último acesso em 20/06/20)
➨ Licenças sob Domínio público via Wikimedia Commons