Reencontrando triângulos retângulos
 |
Apresentaremos aqui algumas definições e propriedades básicas para ajudar no entendimento da trigonometria dos triângulos retângulos. |
Um vídeo para começar…
Para assistir, é só clicar na setinha.
Tudo o que necessitamos nas discussões sobre a trigonometria dos triângulos retângulos apareceu no vídeo que vocês acabaram de assistir.
Vamos, então, passar a limpo as ideias que nos interessam.
Triângulos retângulos e seus elementos
Vamos relembrar o que são triângulos retângulos?
Definição:
Um triângulo retângulo é qualquer triângulo que tenha um ângulo reto, isto é, um ângulo de 90 graus.
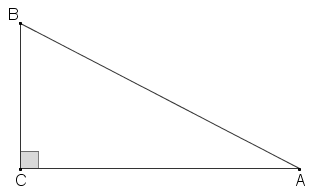 |
Se na figura o ângulo relativo ao vértice [tex]C[/tex] é reto, então o triângulo [tex]ABC[/tex] é um triângulo retângulo. Os lados de um triângulo retângulo recebem denominações especiais. Assim, no triângulo [tex]ABC[/tex]: ● os lados [tex]\overline{CB} \, [/tex] e [tex] \, \overline{CA}[/tex] são denominados catetos; ● o lado [tex] \, \overline{AB}[/tex], oposto ao ângulo reto, é denominado hipotenusa. |
Para simplificar notações, é comum confundir o segmento com sua medida. Assim podemos dizer, por exemplo, que [tex]AB \, [/tex] é a hipotenusa ou que [tex]CB \, [/tex] e [tex] \, CA[/tex] são catetos, sendo [tex]AB[/tex], [tex]CB \, [/tex] e [tex] \, CA[/tex], respectivamente, os comprimentos dos segmentos [tex]\overline{AB}[/tex], [tex]\overline{CB} \, [/tex] e [tex] \, \overline{CA}[/tex].
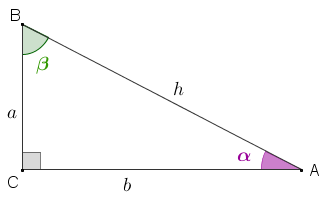
Dessa forma, se [tex]\alpha \, [/tex] e [tex] \, \beta[/tex] são as medidas dos ângulos agudos [tex]\widehat{A} \, [/tex] e [tex]\widehat{B}[/tex] do triângulo retângulo [tex]ABC[/tex], podemos chamar:
|
● [tex]\overline{AB} \, [/tex] ou [tex] \, AB \, [/tex] ou [tex] \, h \, [/tex] de hipotenusa do triângulo [tex]ABC[/tex]; ● [tex]\overline{CB} \, [/tex] ou [tex] \, CB[/tex] ou [tex] \, a[/tex] de cateto oposto a [tex]\widehat{A} \, [/tex] ou a [tex]\alpha \, [/tex]; ● [tex]\overline{CA} \, [/tex] ou [tex] \, CA[/tex] ou [tex] \, b[/tex] de cateto adjacente a [tex]\widehat{A} \, [/tex] ou a [tex]\alpha \, [/tex]; ● [tex]\overline{CB} \, [/tex] ou [tex] \, CB[/tex] ou [tex] \, a[/tex] de cateto adjacente a [tex]\widehat{B} \, [/tex] ou a [tex]\beta \, [/tex]; ● [tex]\overline{CA} \, [/tex] ou [tex] \, CA[/tex] ou [tex] \, b[/tex] de cateto oposto a [tex]\widehat{B} \, [/tex] ou a [tex]\beta \, [/tex]. |
 |
O teorema de Pitágoras
O Teorema de Pitágoras é um dos resultados mais utilizados da matemática e talvez o mais “popular”. Apesar de levar o nome do matemático grego Pitágoras de Samos (569 a.C. – 480 a.C., aproximadamente), este resultado, ao que parece, foi descoberto de maneira independente por vários povos antigos.
Este é o enunciado mais conhecido do teorema:
Em qualquer triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
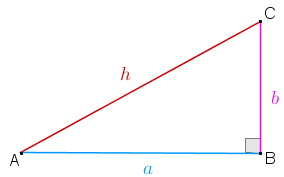 |
Com relação ao triângulo retângulo [tex]ABC[/tex] da figura ao lado, a versão 1 do Teorema de Pitágoras nos garante que: [tex]\qquad \qquad \boxed{a^2+b^2=h^2}[/tex]. É incrível podermos relacionar o comprimento dos lados de um triângulo retângulo, sem sequer conhecê-los! |
Incrível também é a interpretação geométrica dessa formulazinha!
Interpretação Geométrica do Teorema:
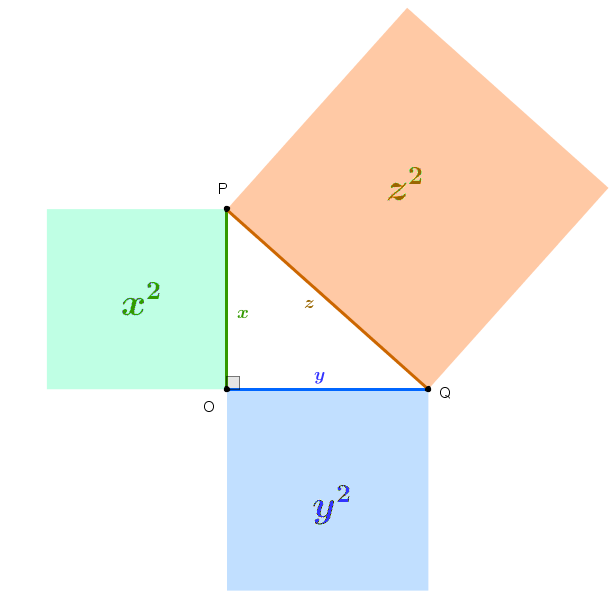
Podemos interpretar geometricamente esse enunciado do Teorema de Pitágoras, utilizando áreas, e garantir que a soma das áreas dos quadrados construídos sobre os catetos de um triângulo retângulo é igual à área do quadrado construído sobre a hipotenusa desse triângulo.
Assim, na figura ao lado, a área verde somada com a área azul é igual à área alaranjada, ou seja:
[tex]\qquad\qquad x^2+y^2=z^2[/tex].
O que chamamos de versão 1 do Teorema de Pitágoras é, sem dúvida, a mais conhecida maneira de se enunciar o Teorema; mas, o que muitas pessoas que utilizam essa versão não sabem é que a recíproca do enunciado é também válida, ou seja:
Recíproca da versão 1 do teorema de Pitágoras
Se em um triângulo o quadrado da medida de um dos lados é igual à soma dos quadrados das medidas dos outros dois, então esse triângulo é retângulo.
Simbolicamente, essa recíproca garante que se [tex]m, \, n, \, t[/tex] são os comprimentos dos lados de um triângulo e [tex]m^2 + n^2=t^2[/tex], então tal triângulo é um triângulo retângulo. Nesse caso, o lado com medida [tex]t[/tex] é a hipotenusa do triângulo em questão.
A versão 1 e sua recíproca podem ser escritas simultaneamente. Vejam, então, uma segunda versão do Teorema de Pitágoras.
Em um triângulo, o quadrado do comprimento de um dos lados é igual à soma dos quadrados dos outros dois lados se, e somente se, o triângulo for retângulo.
Utilizando linguagem mais matemática:
Sejam [tex]a, \, b \, [/tex] e [tex] \, c[/tex] os comprimentos dos lados de um triângulo, com [tex]a, \, b\lt c[/tex]. Então:
tal triângulo é retângulo se, e somente se, [tex]a^2 + b^2=c^2[/tex].
Aparatos para estudar
Não nos preocuparemos com demonstrações nesta sala, já que o nosso objetivo neste momento é, apenas, relembrarmos alguns fatos relacionados à geometria dos triângulos retângulos. Mas, se for conveniente, vocês podem:
[tex](i)[/tex] utilizar as figuras sugeridas abaixo para fazer uma demonstração da versão 1 do Teorema de Pitágoras. As figuras falam por si; mas, como dica, escrevam a área do quadrado de lado [tex]a+b[/tex] de acordo com as duas decomposições sugeridas.
[tex] (ii)[/tex] utilizar o applet disponibilizado para visualizar a interpretação geométrica sobre a qual comentamos. Cliquem no botão do meio e esperem o aplicativo carregar (ele irá abrir em outra janela). Em seguida, movimentem os pontos A, B e C do aplicativo para obterem diferentes triângulos retângulos e comprovarem, particularmente, o Teorema de Pitágoras. Lembrem-se de que o GeoGebra trabalha com aproximações (utilizamos 4 casas decimais).
[tex] (iii)[/tex] assistir ao vídeo e ver uma demonstração experimental do teorema. Tentem justificar o que a experiência tem a ver com o Teorema de Pitágoras.
Boa diversão!
| Figuras | APPLET | Vídeo |
Um vídeo para terminar…
Para assistir, é só clicar na setinha.
Equipe COM – OBMEP
