caleidociclos, Escher e, até,
Tópicos – Sala 1
I – Apresentação do Tema
Vocês já devem ter visto ou, pelo menos, ouvido falar em mosaicos. Os mosaicos podem ser encontrados no artesanato, em utensílios de uso doméstico, pisos, janelas, interior de igrejas, palácios e diversos locais diferentes. Foram utilizados por gregos, romanos, chineses e outros povos para a decoração, principalmente os de motivos religiosos, pois muitos apresentam padrões estéticos harmoniosos, que agradam nosso senso estético.
O mosaico de que estamos falando aqui é a imagem criada pela junção de pequenos fragmentos de materiais (às vezes muito pequenos, às vezes não tão pequenos) que, colados próximos uns dos outros, produzem os mais variados desenhos. Os fragmentos podem ser obtidos de pedras, azulejos de várias cores, pastilhas de vidro e até de papéis, botões, plásticos, entre outros.
|
|
 |
 |
| Mosaico Árabe | Mosaico Grego | Mosaico Bizantino |
Cliquem sobre as figuras para ampliá-las. Depois de visualizar a figura, não se esqueçam de fechar a janela que se abriu.
Esse tipo de arte é muito antigo e teve origem no Oriente. O mosaico considerado pelos historiadores como o mais antigo que se tem conhecimento é o conhecido como Estandarte de Ur – um artefato de mais de 4500 anos, na forma de uma caixa trapezoidal, com várias imagens registradas em suas laterais que contam situações como a guerra e a vida doméstica de um rei.
 Para conhecer um pouco sobre a história do Estandarte de Ur, Para conhecer um pouco sobre a história do Estandarte de Ur,assista a este vídeo. Depois de assistir, não se esqueça de fechar a janela que se abriu. |

|

|
Um mosaico não tão antigo, mas não menos famoso, é o desenho de ondas, imitando o mar, mostrado na imagem abaixo. Essa é a marca registrada do bairro de Copacabana, no Rio de Janeiro, e tornou-se um logotipo internacional.

O desenho original, não tão suave quanto esse, foi trazido pelos calceteiros portugueses e as “ondas” originais eram modestas em sua curvatura e perpendiculares às ondas do mar.
Na década de 1970, o calçadão da Avenida Atlântica foi redesenhado pelo paisagista Roberto Burle Marx, que inverteu a posição do desenho, deixando as ondas de pedra paralelas às ondas do mar, e fez as curvas mais sensuais.
Para saber mais sobre esse mosaico tão famoso, visite a página
Calçadas de pedras portuguesas em Copacabana.
E para quem só conhece o arquiteto e paisagista Burle Marx, visite esta página também: Burle Marx, o mosaicista da pedra e da pastilha.
Nas imagens acima podemos distinguir dois tipos de mosaicos: um apresenta uma imagem criada com a incrustação de pequenas peças coloridas sobre uma superfície e outro tipo que utiliza figuras geométricas criando um padrão que não deixa espaços vazios. Esse último tipo de mosaico é também chamado de pavimentação do plano e será o tema central desta Sala de Atividades. Mais uma vez,
II – Pavimentação do Plano
A história da pavimentação do plano, ou ladrilhamento, é mais antiga que a dos mosaicos, já que desde 4.000 a.C. os antigos egípcios utilizavam ladrilhos na decoração de templos e das grandes pirâmides, enquanto outras civilizações antigas, também, utilizaram ladrilhos em templos e castelos. Muitas dessas construções são admiradas pela humanidade como obras de arte, até hoje. No entanto, o estudo das propriedades matemáticas das pavimentações por polígonos é recente e muitas partes deste tema permanecem ainda por explorar. O astrônomo Joannes Kepler (1571-1630) parece ter sido o pioneiro no estudo da geometria das pavimentações. A partir dos trabalhos de Platão e Arquimedes, Kepler apresenta uma classificação das pavimentações usando polígonos, na qual prova a existência de onze tipos de pavimentação.
Mas o que é uma pavimentação do plano?
● Os vértices dos polígonos são chamados de nós da pavimentação.
● Os segmentos de retas que têm por extremos dois nós consecutivos de um mesmo lado de polígono são chamados de arestas.
● Os polígonos utilizados em uma pavimentação são chamados de ladrilhos.
De maneira mais informal, pavimentar ou ladrilhar um plano é o mesmo que preenchê-lo com polígonos sem deixar espaço entre eles e sem sobrepô-los. Assim, dois polígonos de uma pavimentação só podem ter em comum, no máximo, arestas.
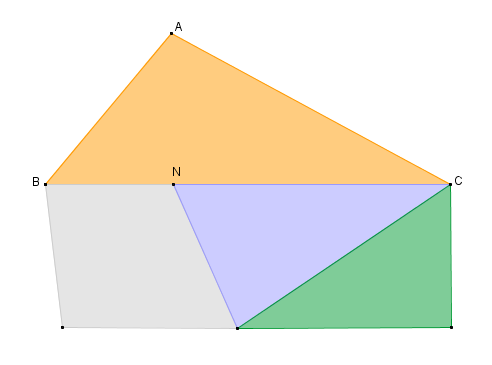
| Importante: Em uma pavimentação, um lado de um polígono pode conter um nó que não seja um de seus vértices; logo, um polígono de uma pavimentação pode conter em seus lados mais nós do que os seus vértices. É possível, também, que a aresta de uma pavimentação não seja lado de um polígono que contenha os nós que definem a aresta. Observem na figura abaixo que [tex]N[/tex] é um nó da pavimentação que pertence ao lado [tex]BC[/tex], mas não é vértice do triângulo [tex]ABC[/tex] e nem a aresta [tex]BN[/tex] é lado desse triângulo. |
 As pavimentações têm várias classificações, como por exemplo:
As pavimentações têm várias classificações, como por exemplo:
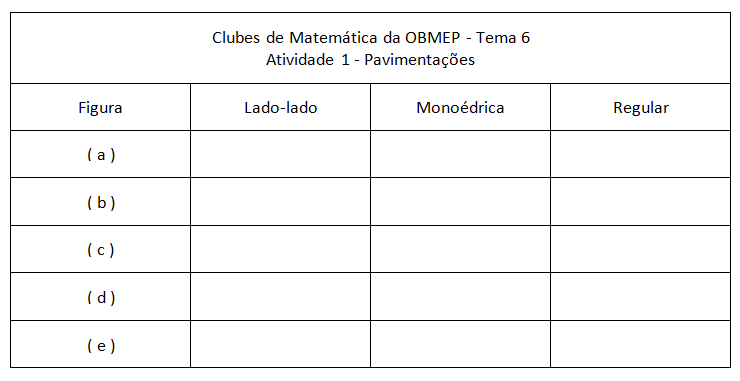
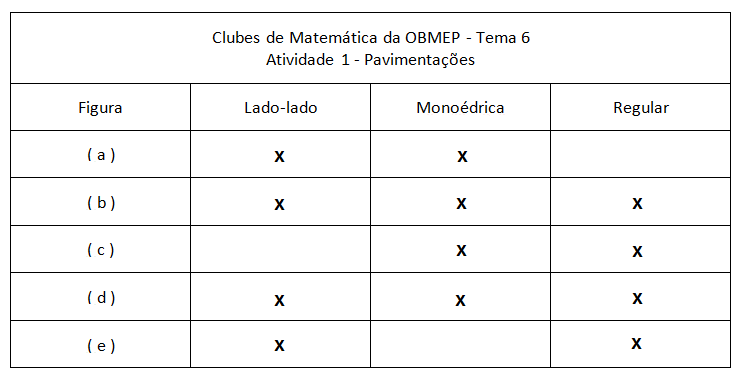
● Lado-lado: Pavimentações nas quais toda aresta é lado comum a dois polígonos e assim todo nó na aresta de um polígono da pavimentação é vértice desse polígono.
● Monoédricas ou puras: São pavimentações constituídas de polígonos congruentes entre si.
● Regulares: São pavimentações monoédricas e lado-lado nas quais os ladrilhos são polígonos regulares.
Será que vocês entenderam direitinho essas três classificações de pavimentações? Para saber, tentem fazer a atividade a seguir.
Atividade 1
Vocês podem conferir suas respostas, clicando no botão abaixo.
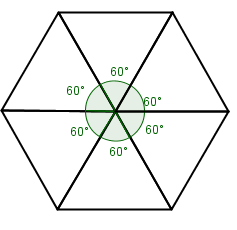
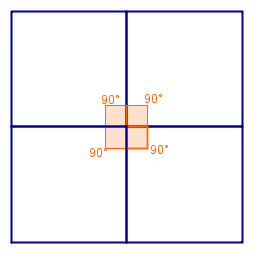
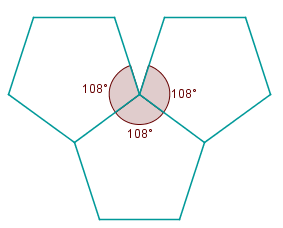
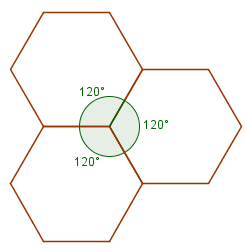
As pavimentações do plano mais simples são as regulares, ou seja, as pavimentações monoédricas, lado-lado e cujos ladrilhos são polígonos regulares. Além de estas pavimentações possuírem um único tipo de ladrilho, o uso da expressão “mais simples” ficará mais claro depois de respondermos à seguinte pergunta:
Que tipo de polígono regular pode ser utilizado em uma pavimentação regular?
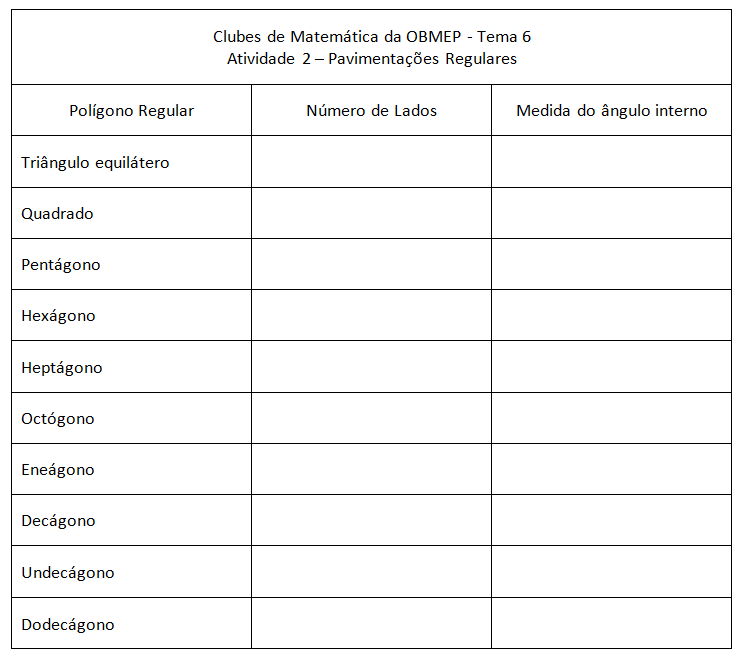
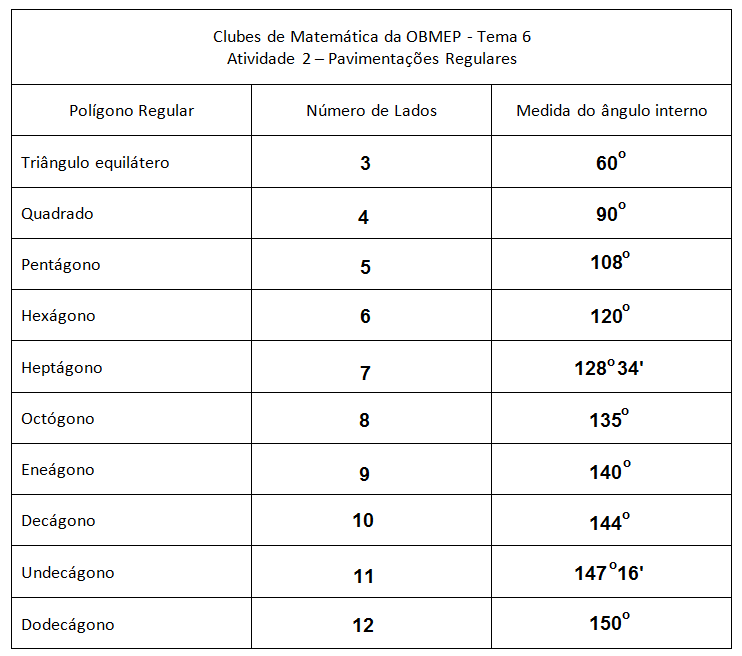
Como a resposta para essa pergunta depende, essencialmente, da medida do ângulo interno do tipo de polígono regular da pavimentação, sugerimos que vocês tentem obter as medidas dos ângulos internos de alguns polígonos regulares. Para isso, deixamos aqui mais uma atividade.
Atividade 2
Precisam de ajuda?
Confiram suas respostas, clicando no botão abaixo.
Feita a atividade, já podemos buscar a resposta sobre que polígonos podem ser utilizados em pavimentações regulares.
Acompanhem a discussão, clicando no botão abaixo.
As pavimentações lado-lado cujos ladrilhos são regulares, mas não congruentes entre si, podem ser denominadas de pavimentações quase regulares ou pavimentações arquimedianas. É possível mostrar de maneira não muito complicada que existem apenas oito pavimentações desse tipo, ou seja, oito pavimentações lado-lado cujos ladrilhos são polígonos regulares de mais de um tipo. Assim são apenas onze as pavimentações formadas por polígonos regulares não necessariamente congruentes. Se vocês se interessaram pelo assunto, indicamos o seguinte texto:
❏ LADRILHAMENTOS
Élvia Mureb Sallum
Para conhecer pavimentações monoédricas definidas por triângulos, quadriláteros e hexágonos, não necessariamente regulares, assim como vários resultados gerais sobre pavimentação, leiam o texto:
Algumas pavimentações do plano podem ser visualizadas utilizando-se um objeto que já encantou crianças e adultos ao redor do mundo durante muito tempo, mas, que nos dias de hoje, está esquecido: o caleidoscópio.
Vamos conhecer um pouco sobre caleidoscópios?
III – Caleidoscópio

David Brewster (1781 – 1868)
O cientista escocês David Brewster, por volta de 1816, estudava alguns aspectos das ciências físicas, incluindo óptica e as propriedades da luz, quando inventou o caleidoscópio. Ele nomeou sua invenção usando as palavras gregas:
kalos = bonita eidos = forma scopos = observador.

Caleidoscópio poli-angular de David Brewster
Por suas descobertas científicas, David Brewster foi eleito membro da Royal Society em 1815 e nomeado cavaleiro em 1831. Além de inventar e nomear o caleidoscópio, Sir David Brewster também usou polarização e espelhos poli-angulares em seus caleidoscópios. No entanto esses elementos não foram utilizados em outros caleidoscópios até a década de 1980 – 150 anos mais tarde.
Durante a década de 1870, na Inglaterra, o caleidoscópio era objeto de luxo, estando presente nas casas mais elegantes. Mas isso mudou com a era eletrônica do rádio e, posteriormente, da televisão.
Em meados dos anos 1900, o caleidoscópio difundiu-se como brinquedo infantil. Uma firma de brinquedos, fundada em 1946, foi um dos produtores mais famosos de caleidoscópios nos Estados Unidos e os fabricam até hoje.
A Era Moderna do Caleidoscópio
A popularidade do caleidoscópio aumentou novamente no final da década de 1970. O ressurgimento desse objeto foi uma combinação de artesanato e avanços tecnológicos. Durante os anos 80 e 90, artistas começaram a trabalhar tanto a parte interna como a parte externa do caleidoscópio. Os exteriores foram feitos de novos materiais, como vidro soprado à mão e cerâmica, entre outros. Também foram utilizados materiais diferentes (ou mesmo estranhos) como cabaças, garrafas de vinho e de cerveja e até peças de motocicletas.
 Modelos de caleidoscópios de brinquedo
Modelos de caleidoscópios de brinquedo
Mas, independente de como é construído, as imagens que os caleidoscópios produzem
são belíssimas, não há como negar…

|

|
 |

|
É hora de vocês construírem um caleidoscópio
e captar suas próprias imagens…
IV – Caleidociclos
O que vocês acham de conseguir quatro padrões diferentes
de pavimentação, a partir de um único padrão?
Parece uma boa ideia, não é?
Se vocês ficaram curiosos, então leiam com atenção as informações deste tópico, pois nele vamos tratar dos caleidociclos. O caleidociclo é um anel tridimensional feito em papel e formado por tetraedros unidos por suas arestas; ele pode girar infinitas vezes sobre si próprio, em torno de seu centro, sem se romper ou deformar, produzindo belos efeitos visuais.

Embora a ideia do objeto seja mais antiga, o nome caleidociclo foi utilizado pela primeira vez em 1977 para designar esse objeto e deriva do grego:
kalós (belo) + eidos (forma) + kyklos (ciclo)
resultando, de fato, no que o objeto é: uma bela forma cíclica!
Podemos encontrar dois tipos básicos de caleidociclos: o hexagonal e o octogonal (ou quadrado). As denominações vêm da forma do polígono resultante de cada ciclo de movimentos: um hexágono ou um octógono, respectivamente.
 |
 |
| caleidociclo hexagonal | caleidociclo octogonal |
Os vídeos mostram os dois tipos de caleidociclos em movimento real, já que eles devem ser movidos manualmente.
| caleidociclo hexagonal | caleidociclo octogonal |
Ao vermos um caleidociclo sendo movimentado, a primeira impressão é que se trata de um objeto muito difícil de ser construído.
Mas não é! (Cá para nós, é muito mais fácil do que um caleidoscópio)
Então, que tal vocês tentarem construir um? Essa construção será a nossa próxima atividade.
V – E a matemática ???
Que objeto matemático é um caleidociclo?
Alguns de vocês devem estar com a resposta na ponta da língua: Um caleidociclo é um poliedro!
Outros já estão, até, se adiantando e contando arestas, vértices e faces dos caleidociclos construídos para comprovar, mais uma vez, que [tex]V-A+F=2 [/tex]: afinal, alguém em sã consciência duvidaria de Euler ?
É sempre bom lembrar que na matemática, antes de classificarmos um objeto disso ou daquilo, temos que saber precisamente o que significam o isso e o aquilo em questão. E, particularmente, o estudo dos poliedros é um tópico da matemática no qual comumente as pessoas saem classificando objetos sem, de fato, saber quais as características que um objeto deve ter para receber determinada classificação, ou um determinado nome. Só para vocês terem uma ideia do tamanho da confusão que isso causa, dependendo do que classificamos como poliedro, a relação de Euler pode não ser satisfeita, já que poliedro é um objeto matemático que pode ser definido com diferentes níveis de generalidade.
Assim, para evitar problemas, sugerimos que vocês cliquem no botão abaixo, antes de prosseguir…
De volta aos caleidociclos, finalizamos esta Sala deixando para vocês mais uma atividade. Cliquem neste último botão e, se necessário, visitem novamente a sala sobre poliedros.
Bom trabalho, pessoal!
 |
Visite a Sala 2 do Tema!
|
Equipe COM – OBMEP
Outubro de 2015.
➨ Arte em Toda a Parte (Último acesso em 18/08/20)
➨ Brasil Escola (Último acesso em 18/08/20)
➨ Caleidoscópio (Último acesso em 18/08/20)
➨ Dreamstime (Último acesso em 18/08/20)
➨ Engenharia de papel (Último acesso em 18/08/20)
➨ Flickr (Último acesso em 18/08/20)
➨ História do Mosaico (Último acesso em 18/08/20)
➨ O incrível Estandarte de Ur (Último acesso em 25/09/15)
➨ Para divertir os pequenos: aprenda a fazer um caleidoscópio (Último acesso em 18/08/20)
➨ Paula Nadelstern, el Arte del Caleidoscopio (Último acesso em 18/08/18)
➨ PAVIMENTAÇÕES NO PLANO EUCLIDIANO (Último acesso em 25/08/20)
➨ Totally History (Último acesso em 18/08/20)
➨ YouTube (Último acesso em 18/08/20)
➨ Licenças sob Domínio público via Wikimedia Commons
➨ Wikimedia – David Brewster Commons (Último acesso em 18/08/20)