b_Kepler

Johannes Kepler

Johannes (ou Johanes, ou Joannes) Kepler nasceu em 27 de dezembro de 1571, em Weil der Stadt, na Alemanha, e faleceu em 15 de novembro de 1630, em Ratisbona, Alemanha. Foi um astrônomo e matemático que, durante sua existência, trouxe importantíssimas contribuições para a ciência. Dentre algumas dessas, formulou três leis fundamentais da mecânica celeste, que hoje são conhecidas como Leis de Kepler.

Graduou-se pela Universidade de Tübingen e, durante sua carreira, foi professor de matemática na Universidade de Graz, Áustria.

Em 1600, foi obrigado a deixar a cidade de Graz, perseguido por ser protestante. Estabeleceu-se, então, na cidade de Praga, onde se tornou assistente do astrônomo Tycho Brahe, e matemático da corte do imperador Rodolfo II.

Em 1612 foi nomeado professor de matemática em Linz, Áustria.

Kepler também teve uma participação relevante no campo da óptica, quando propôs uma versão ainda melhor do telescópio refrator de Galileu (hoje conhecido como Telescópio de Kepler), além de ter ajudado a ratificar algumas descobertas telescópicas do grande astrônomo Galileu Galilei.

Obra

● Órbitas Elípticas

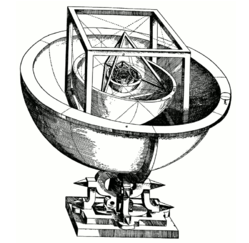
De formação profundamente religiosa, Kepler via Deus como o poder criador do Cosmos. Descobrir os segredos do universo era para ele um jogo que ele jogava com Deus. Apesar de suas convicções cristãs, Kepler inclinou-se para as ideias de Copérnico, aderindo ao sistema heliocêntrico do universo, em contraposição à teoria oficial da Terra como centro imóvel do cosmo. Apesar da sua fé, Kepler não achou que um universo heliocêntrico fosse uma heresia; pelo contrário, nesse modelo o Sol parecia ser uma metáfora de Deus, à volta de Quem tudo gira. O primeiro grande trabalho sobre astronomia de Johannes Kepler, Mysterium Cosmographicum (O Mistério Cosmográfico, 1956), foi a primeira defesa publicada do sistema copernicano. Nesta obra, Kepler procurou associar os planetas aos cinco sólidos platônicos, (tetraedro, cubo, octaedro, dodecaedro e icosaedro, com 4, 6, 8, 12 e 20 faces iguais, respectivamente), buscando uma lei geométrica universal que descrevesse o conjunto de suas órbitas.

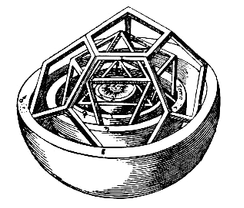O modelo de Kepler dos sólidos platônicos para o Sistema Solar	Detalhe central

Suas observações levaram-no a convencer-se da existência de uma força que conserva os planetas em suas órbitas ao redor do Sol e suas publicações neste sentido chamaram a atenção para seu autor, que passa a corresponder-se com os mais eminentes astrônomos da época, como Tycho Brahe e Galileu. Fruto de suas constantes observações do planeta Marte, Kepler publica, em 1609, uma de suas obras fundamentais: Nova astronomia. Impressionado com a variação dos movimentos de Marte e estudando os trabalhos de Brahe, ele chega a uma conclusão que rompe com as opiniões de um milênio de estudos astronômicos: os movimentos dos astros celestiais são elípticos e não, como se imaginava, circulares.

● As Leis de Kepler

Duas das três leis que passariam a ser conhecidas pelo nome do astrônomo foram publicadas em Nova Astronomia. A terceira se encontra no livro Sobre a harmonia do mundo (1619), obra que, cinquenta anos depois, permitiria a Newton a descoberta da Lei da Gravitação Universal.

As três leis de Kepler podem ser assim resumidas:
1ª) as órbitas dos planetas em torno do Sol são elipses, nas quais o Sol ocupa um dos focos;
2ª)no movimento de cada planeta, as áreas varridas pelo raio vetor que une o planeta ao Sol são proporcionais ao tempo gasto para percorrê-las;
3ª) os quadrados dos tempos das revoluções siderais dos planetas são proporcionais aos cubos dos grandes eixos de suas órbitas.

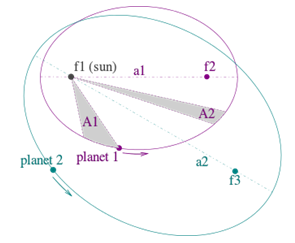As leis de Kepler, com duas órbitas planetárias: (1) As órbitas são elipses, com pontos focais f1 e f2 para o planeta 1 e f1 e f3 para o planeta 2. O sol está no ponto focal f1. (2) Os dois setores sombreados A1 e A2 possuem a mesma área superficial e o tempo para o planeta 1 varrer o setor A1 é igual ao tempo para varrer o setor A2. (3) A relação entre os períodos dos planetas 1 e 2 está na proporção a1[tex]^{\frac{3}{2}}[/tex]:   a2[tex]^{\frac{3}{2}}[/tex].

Depois de Sobre a harmonia do mundo, Kepler se dedica à preparação de um mapa que representasse, com a precisão possível na época, as posições planetárias. O resultado é a obra Tábuas Tudolfinas (1623), iniciada por Tycho Brahe e utilizada por mais de um século no cálculo das posições planetárias.

Muitas das ideias de Kepler levaram anos para serem compreendidas. Dentre elas, sua observação de que a velocidade de um astro aumenta em relação direta à proximidade de seu ponto de atração, o que foi elucidado pela Lei da Gravitação e por outras observações do cosmo.

● Um presente de Ano Novo

Como presente de Ano Novo, em 1611, Kepler compôs para seu amigo e há algum tempo patrono, Baron Wackher von Wackhenfels, um pequeno folheto intitulado Strena Seu de Nive Sexangula (Um Presente de Ano Novo de Neve Hexagonal). Neste tratado, Kepler publicou a primeira descrição da simetria hexagonal dos flocos de neve e estendeu a discussão para uma hipotética base física atomística para a simetria, enunciando o que mais tarde ficou conhecida como a conjectura de Kepler:

a melhor maneira de se empilhar objetos esféricos seria organizá-los na forma de pirâmide.

Foi Thomas Hales, da Universidade de Pittsburgh (EUA), quem desenvolveu uma prova para o problema, em 1998. Hales quebrou o problema em milhares de arranjos possíveis e utilizou um software para resolver todos. No entanto, o trabalho final ficou com 300 páginas, e foram necessários muitos revisores e alguns anos para verificar se havia algum erro. Mesmo assim, quando o estudo foi publicado na revista Annals of Mathematics em 2005, os cientistas estavam apenas 99% seguros de que o resultado estava correto. Em 2003, Hales começou a criar o projeto “Flyspeck”, uma ferramenta computacional capaz de verificar sua prova. Então, em 2014, um computador finalmente mostrou que a ideia do astrônomo e matemático Kepler era verdadeira.

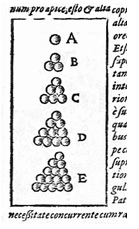
Um dos diagramas de Strena Seu de Nive Sexangula, ilustrando a conjectura de Kepler.

● Infinitesimais

Kepler foi um dos pioneiros em relação às aplicações matemáticas dos infinitesimais. Segundo John Kirkby (1735), um infinitesimal é “aquilo que é infinitamente menor que qualquer quantidade concebível; é como um grão de sal comparado com o globo terrestre, ou um instante de tempo comparado com um milhão de eras”. Como consequência, quaisquer quantidades cuja diferença seja um infinitesimal devem ser consideradas iguais. Infinitesimais foram usados na definição original da derivada (conceito intimamente ligado à taxa de variação instantânea de uma quantidade em função de outra), dada por Leibniz.

Homenagem

KEPLER MISSION SCIENTIFIC – A missão Científica Kepler (NASA)

Em 1984, os cientistas Bill Borucki e A. L. Summers publicaram um artigo intitulado “O método fotométrico de detectar outros sistemas planetários”. Surgia, então, a ideia para a Missão Kepler, da NASA.

A sonda Kepler consiste em um observatório espacial que procura por planetas extrassolares (um exoplaneta ou planeta extrassolar é um planeta que orbita uma estrela que não seja o Sol e, desta forma, pertence a um sistema planetário distinto do nosso). O objetivo científico da missão Kepler é explorar a estrutura e diversidade de sistemas planetários. Neste sentido, a bem-sucedida missão conta com inúmeras descobertas já realizadas. Johannes Kepler é considerado o primeiro astrofísico e a Missão Kepler o honra por suas realizações, além de utilizar a terceira lei de Kepler para determinar o tamanho das órbitas planetárias.

Em 2015, a Missão Kepler descobriu um exoplaneta com características semelhantes ao nosso: Kepler-452b, ao qual a agência espacial americana chamou de “primo mais velho” da Terra.