Sala de Atividades: Pavimentação – Sala 2

Tópicos – Sala 2

VI – Escher

Vocês já ouviram falar de um artista gráfico chamado Escher?

Bem, aqui nos Clubes de Matemática da OBMEP vocês já devem ter se deparado com alguns vídeos a respeito dele. Na Videoteca dos Clubes temos o vídeo Inspirations, do cineasta espanhol Cristóbal Vila que imagina como seria o local de trabalho do artista, e o vídeo Escher e a Geometria – um passeio pela exposição “O mundo mágico de Escher”, que ficou em cartaz em São Paulo em julho de 2011.

Caso ainda não conheçam Escher, vale a pena assistir aos vídeos!!

Maurits Cornelis Escher (1898-1972) é um dos mais famosos artistas gráficos do mundo e seus trabalhos são encontrados em muitos sites da Internet. Ele ficou conhecido, principalmente, pelas construções impossíveis presentes em suas obras, como as duas apresentadas a seguir.

Mas não é por suas construções impossíveis que Escher está nesta Sala. Nos dias de hoje, não podemos falar de pavimentação do plano sem citá-lo.

Desde a sua primeira visita a um castelo Mouro em Granada, Espanha, no ano de 1922, Escher se inspirou nos azulejos espanhóis e se interessou pela divisão regular do plano, criando várias pavimentações. Para conhecer um pouco mais sobre o envolvimento de Escher com a pavimentação, assistam ao vídeo O estranho mundo de Escher, da série Isto é Matemática.

Vamos, então, conhecer um pouquinho sobre
o imenso e maravilhoso “estranho mundo das pavimentações de Escher”.

VII – Um pouco sobre as pavimentações de Escher

Escher explorou de forma brilhante a geometria plana e a geometria espacial em suas obras, mesmo não tendo qualquer formação ou conhecimento de ciências exatas. O seu encanto por figuras geométricas e padrões levou-o a descobrir a Teoria da Divisão do Plano Regular: uma superfície pode ser dividida regularmente em figuras iguais e totalmente preenchida com elas sem a existência de espaços vazios.

Essa técnica já era dominada por povos antigos, que a utilizavam na confecção de seus mosaicos, conforme vimos na Sala 1; mas Escher foi além dos triângulos equiláteros, quadrados e hexágonos regulares capazes de cobrir o plano sem deixar buracos ou se sobreporem. Ele substituiu os polígonos regulares por figuras que representam coisas existentes na natureza – pessoas, pássaros, peixes, répteis, etc. – e criou imagens envolventes, como as que vemos abaixo.

MC Escher: Plane Filing II, 1957	MC Escher: Horse, 1937-1938	MC Escher: BirdFish, 1941
MC Escher: Fish, 1942	MC Escher: Two-Fish, 1942	MC Escher: Eagle, 1938
MC Escher: IMP, 1938	MC Escher: Lizard, 1939	MC Escher: Three-Birds, 1938

Imagens extraídas de: M.C.Escher

Muito embora os únicos polígonos regulares que são possíveis de serem utilizados para pavimentar o plano sejam o triângulo, o quadrado e o hexágono, Escher combinou, deslocou, girou, refletiu e distorceu essas três figuras matemáticas, obtendo uma maior variedade de padrões e criando pavimentações mais elaboradas. As três palavras em negrito deslocou, girou e refletiu representam o resultado de três ações possíveis de se fazer em um plano de modo que uma figura sobre a qual elas foram aplicadas muda de posição, mas não de forma. Na matemática, essas ações são estudadas e recebem, respectivamente, os seguintes nomes: translação; rotação; reflexão.

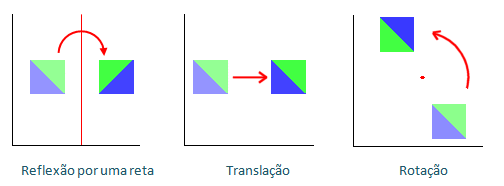
Para relembrar um pouco sobre elas, cliquem AQUI.

Mesmo desenhando pássaros, peixes e outros animais para dar vida às suas pavimentações, Escher não abandonou os polígonos; pelo contrário, utilizou-os como base para gerar as figuras que compuseram suas pavimentações. Assim, desenhando dentro de polígonos e utilizando degradees de cores e sombras, criou padrões que ficaram conhecidos como metamorfoses (gradativamente, uma figura vai se transformando em outra). Um exemplo dessa técnica vocês podem ver nas próximas figuras. Clicando sobre a primeira figura, vocês poderão assistir a uma animação que brinca com a obra! Clicando sobre a segunda, vocês poderão assistir a um vídeo mostrando detalhes da obra, que mede 19,2 cm x 680 cm. Isso mesmo, 6,8 metros de comprimento.

Cliquem em uma figura e na janela que irá abrir, é só clicar na setinha. Depois de assistir ao vídeo, é só fechar a janela que se abriu.

MC Escher: Sky and Water, 1938	MC Escher: Metamorfoses II, 1967-1968

VIII – Treinando para ser um Escher

Escher criava padrões e efeitos surpreendentes a partir de formas geométricas básicas.
Com esta atividade vamos procurar objetos matemáticos disfarçados de arte.

	Esta é uma bela forma para se criar um padrão de pavimentação, não é? Mas vamos explorá-la matematicamente com uma única pergunta: Sabendo que as curvas que definem a figura são semicircunferência de mesmo raio, vocês saberiam calcular a área dessa figura? Se não sabem, acompanhem as sugestões.
	Suponham que vocês conheçam as distâncias entre os pontos A, B e C. Ajudou?
	Suponham que vocês saibam que as distâncias entre os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] são iguais. Nada, ainda?
	Última dica, hem? Suponha que [tex]\qquad d(A,B) = d(B,C) = d(C,A) = d[/tex], una os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] por segmentos de reta e calcule a área em função de [tex]d[/tex]. Agora é com vocês!

Esta era uma das técnicas utilizadas por Escher para desenhar seus padrões de pavimentação.

IX – Um dia de Escher

E aí, prontos para um dia de Escher?

Vamos lá, cliquem neste último botão.

Bom trabalho, pessoal!

Boa diversão!!!