Clique no botão abaixo para visualizar a Sala.
Atividades
I – Um vídeo para começar
Vimos na Sala Principal que a força de um terremoto pode ser medida pela sua magnitude e pela sua intensidade: “a magnitude está associada com a energia liberada pelo terremoto”, enquanto “a intensidade é o efeito causado por ele na superfície da Terra”. Assim, quando falamos sobre “calcular a energia liberada por um sismo”, estamos considerando a magnitude e não a intensidade do terremoto.
Vamos recordar?
II – Atividades Individuais
Vamos treinar um pouco com problemas que envolvem a aplicação de logaritmos em terremotos nas provas de vestibulares?
U.S. GEOLOGICAL SURVEY, Historic Earthquakes. Disponível em: http://earthquake.usgs.gov. Acesso em: 1 maio 2010 (adaptado).
U.S. GEOLOGICAL SURVEY. USGS Earthquake Magnitude Policy. Disponível em: http://earthquake.usgs.gov. Acesso em: 1 maio 2010 (adaptado).
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico [tex]M_0[/tex] do terremoto de Kobe (em [tex] dina.cm[/tex])?
a) [tex]10^{-5,10}.[/tex]
b) [tex]10^{-0,73}.[/tex]
c) [tex]10^{12,00}.[/tex]
d) [tex]10^{21,65}.[/tex]
e) [tex]10^{27,00}.[/tex]
Efetuando as operações, obtemos:
[tex]\quad 7,3+10,7=\dfrac{2}{3} \cdot log_{10}(M_0) \\
\quad 18=\dfrac{2}{3} \cdot log_{10}(M_0)\\
\quad 27=log_{10}(M_0) \\
\quad M_0=10^{27}.[/tex]
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre [tex]E_1[/tex] e [tex]E_2[/tex]?
a) [tex]E_1=E_2+2.[/tex]
b) [tex]E_1=10^2 \cdot E_2.[/tex]
c) [tex]E_1=10^3 \cdot E_2.[/tex]
d) [tex]E_1=10^{9/7} \cdot E_2.[/tex]
e) [tex]E_1=\dfrac{9}{7} \cdot E_2.[/tex]
[tex]\qquad \qquad M=\dfrac{2}{3} \cdot log\left(E/E_0 \right) \iff log\left(E/E_0 \right)= \dfrac{3M}{2} \iff \boxed{E=E_0 \cdot 10^{3M/2}}.[/tex]
Daí, como [tex]M_1=9[/tex] e [tex]M_2=7[/tex], temos [tex]E_1=E_0 \cdot 10^{27/2}~[/tex] e [tex]~E_2=E_0 \cdot 10^{21/2}.[/tex]
Portanto, segue que:
[tex]\quad E_1=E_0 \cdot 10^{27/2}\\
\quad E_1=E_0 \cdot 10^{21/2} \cdot 10^{6/2}\\
\quad E_1=E_2 \cdot 10^3.[/tex]

Um terremoto teve sua amplitude e frequências medidas e obteve-se [tex]A=1\ 000[/tex] micrômetros e [tex]f=0,2[/tex] hertz. Use [tex]-0,7[/tex] como aproximação para [tex]log\,0,2.[/tex]
Disponível em: www.mundoeducacao.com.br. Acesso em: 11 jul. 2012 (adaptado).
Considerando o quadro apresentado, e analisando o resultado da expressão que fornece a magnitude desse terremoto, conclui-se que ele foi
a) registrado, mas não percebido pelas pessoas.
b) percebido, com pequenos tremores notados pelas pessoas.
c) destrutivo, com consequências significativas em edificações pouco estruturadas.
d) destrutivo, com consequências significativas para todo tipo de edificação.
e) destrutivo, com consequências nas fundações dos edifícios, fendas no solo e tubulações no subsolo.
[tex]\quad M=log(1\ 000 \cdot 0,2)+3,3\\
\quad M=log10^3+log0,2+3,3\\
\quad M \approx 3-0,7+3,3 \\
\quad M\approx 5,6.[/tex]
Portanto, podemos concluir que ele foi destrutivo, com consequências significativas em edificações pouco estruturadas.
Disponível em: http://oglobo.globo.com. Acesso em: 2 ago. 2012.
A energia liberada pelo terremoto que atingiu a costa nordeste do Japão em [tex]2011[/tex], em [tex]kWh[/tex], foi de
a) [tex]10^{10,83}[/tex]
b) [tex]10^{11,19}[/tex]
c) [tex]10^{14,19}[/tex]
d) [tex]10^{15,51}[/tex]
e) [tex]10^{17,19}[/tex]
[tex]\quad 8,9=\dfrac{2}{3} \cdot log\left(\dfrac{E}{E_0} \right)\\
\quad log\left(\dfrac{E}{E_0} \right)=13,35\\
\quad log~E-log~E_0=13,35\\
\quad log~E=13,35+log~E_0\\
\quad log~E=13,35+log~\left(7 \cdot 10^{-3}\right)\\
\quad log~E=13,35 + log~7+ log~10^{-3 }\\
\quad log~E=13,35 + 0,84-3 \cdot log~10\\
\quad log~E=11,19\\
\quad E=10^{11,19}.
[/tex]
Disponível em: http://earthquake.usgs.gov. Acesso em: 28 fev. 2012 (adaptado).
A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é
a) [tex]1,28[/tex]
b) [tex]2,0[/tex]
c) [tex]10^{9/7}[/tex]
d) [tex]100[/tex]
e) [tex]10^9-10^7[/tex]
[tex]\qquad R=log\left(\dfrac{A}{A_0} \right) \iff \dfrac{A}{A_0}=10^R \iff A=A_0 \cdot 10^R.[/tex]
Logo, se [tex]A_J[/tex] e [tex]A_A[/tex] são, respectivamente, as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina, então:
[tex]\quad \dfrac{A_J}{A_A}=\dfrac{A_0 \cdot 10^9}{ A_0 \cdot 10^7}=100.[/tex]
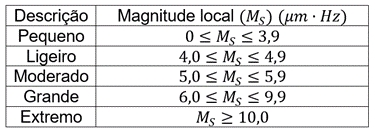
Para se calcular a magnitude local, usa-se a fórmula [tex]M_S=3,30+log(A \cdot f)[/tex], em que [tex]A[/tex] representa a amplitude máxima da onda registrada por um sismógrafo em micrômetro [tex]\mu m[/tex] e [tex]f[/tex] representa a frequência da onda, em hertz [tex](Hz)[/tex]. Ocorreu um terremoto com amplitude máxima de [tex]2\ 000\ \mu m[/tex] e frequência de [tex]0,2\ Hz[/tex].
Disponível em: http://cejarj.cecierj.edu.br. Acesso em: 1 fev. 2015 (adaptado).
Utilize [tex]0,3[/tex] como aproximação para [tex]log\,2[/tex]. De acordo com os dados fornecidos, o terremoto ocorrido pode ser descrito como
a) Pequeno.
b) Ligeiro.
c) Moderado.
d) Grande.
e) Extremo.
[tex]\quad M_S=3,3+log(2\ 000 \cdot 0,2)\\
\quad M_S=3,3+log(2^2 \cdot 10^2)\\
\quad M_S=3,3+log\,2^2+log\,10^2[/tex]
segue que:
[tex]\quad M_S = 3,3+2 \cdot log\,2+2 \cdot log\,10 \approx 3,3 +0,6+2 = 5,9.[/tex]
Dessa forma, podemos concluir que o terremoto ocorrido pode ser descrito como Moderado.
● Em [tex]16[/tex] de setembro de [tex]2015[/tex], um terremoto de magnitude [tex]8,3[/tex] atingiu o Chile, próximo à região de Valparaíso, deixando várias vítimas.
● Em [tex]08[/tex] de setembro de [tex]2017[/tex], um terremoto de magnitude [tex]5,3[/tex] atingiu a região norte do Japão.
Sabendo que os dois terremotos acima tiveram a mesma amplitude [tex]B[/tex] e período [tex]T[/tex], podemos afirmar que com relação à amplitude do movimento vertical do solo, o terremoto no Chile foi
a) [tex]2[/tex] vezes mais forte que o do Japão.
b) [tex]3[/tex] vezes mais forte que o do Japão.
c) [tex]10[/tex] vezes mais forte que o do Japão.
d) [tex]100[/tex] vezes mais forte que o do Japão.
e) [tex]1\ 000[/tex] vezes mais forte que o do Japão.
[tex]\qquad 8,3=log\left(\dfrac{a_{Chile}}{T}\right)+B\\
\qquad 8,3-B= log\left(\dfrac{a_{Chile}}{T}\right)\\
\qquad \dfrac{a_{Chile}}{T}=10^{8,3-B} \\
\qquad \boxed{ a_{Chile} =T \cdot 10^{8,3-B}}.[/tex]
● Para o terremoto do Japão, temos que:
[tex]\qquad 5,3=log\left(\dfrac{a_{Japão}}{T}\right)+B \\
\qquad 5,3-B= log\left(\dfrac{a_{Japão}}{T}\right) \\
\qquad \dfrac{a_{Chile}}{T}=10^{5,3-B} \\
\qquad \boxed{ a_{Japão} =T \cdot 10^{5,3-B}}.[/tex]
Deste modo,
[tex]\quad \dfrac{a_{Chile}}{a_{Japão}}=\dfrac{T \cdot 10^{8,3-B}}{T \cdot 10^{5,3-B}}=10^{8,3-B-(5,3-B)}\\
\quad \dfrac{a_{Chile}}{a_{Japão}} =10^3=1\ 000[/tex]
e, portanto, o terremoto no Chile foi [tex]1\ 000[/tex] vezes mais forte que o do Japão.
Aumentando de uma unidade a magnitude do terremoto, por quanto fica multiplicada a energia liberada?
a) [tex]8 \cdot \sqrt{10}[/tex]
b) [tex]9 \cdot \sqrt{10}[/tex]
c) [tex]10 \cdot \sqrt{10}[/tex]
d) [tex]11 \cdot \sqrt{10}[/tex]
e) [tex]12 \cdot \sqrt{10}[/tex]
[tex]\quad M=\dfrac{2}{3} \cdot log_{10}\left(\dfrac{E}{E_0}\right) \iff log_{10}\left(\dfrac{E}{E_0}\right)=\dfrac{3 \cdot M}{2} \iff \boxed{E=E_0 \cdot 10^\frac{3 \cdot M}{2}}.[/tex]
Com isso, aumentando uma unidade a magnitude do terremoto segue que a energia [tex]E_a[/tex] correspondente é dada por:
[tex]\quad E_a=E_0 \cdot 10^\frac{3 \cdot (M+1)}{2}\\
\quad E_a= \left(E_0 \cdot 10^\frac{3 \cdot M}{2}\right) \cdot 10^\frac{3}{2}\\
\quad E_a=E \cdot \textcolor{red}{10 \cdot \sqrt{10}}.[/tex]
Dessa forma, aumentando de uma unidade a magnitude do terremoto, a energia liberada fica multiplicada por [tex]10 \cdot \sqrt{10}[/tex].
E que tal resolver, agora, alguns problemas gerais envolvendo logaritmos?
Uma emissora de TV resolveu lançar a Kyle Korver um desafio de lances livres, no qual ele deve arremessar seguidas vezes na mesma tabela. Porém, entre um arremesso e outro, ele deve ir até o meio da quadra receber a bola de um fã.
Considerando que a probabilidade de ele acertar um arremesso qualquer nestas condições seja a mesma de sua carreira escolar, a partir de qual lançamento a probabilidade de ele não acertar todos os lances livres torna-se maior que a de ter acertado todos?
Para efeito de cálculos, considere [tex]log(2) \approx 0,3010 \, [/tex] e [tex] \, log(3) \approx 0,4771[/tex].
Solução
[tex]A=\dfrac{1}{3log_2 1500}+\dfrac{1}{6log_3 1500}+\dfrac{1}{2log_5 1500}[/tex].
Solução
Solução
Quantas vezes a tecla [tex]\log[/tex] precisa ser pressionada para que apareça uma mensagem de erro?
Solução
[tex]\begin{cases}
log_{2}(xyz-3+log_{5}x)=5 \\
log_{3}(xyz-3+log_{5}y)=4 \\
log_{4}(xyz-3+log_{5}z)=4
\end{cases}[/tex] .
Sabendo que [tex]xyz[/tex] é um número inteiro, encontre o valor de [tex]|log_{5}x|+|log_{5}y|+|log_{5}z|[/tex].
Solução
Solução
[tex]\qquad \qquad f(n)=\log_{2730} n^2[/tex], com o logaritmo na base [tex]2730.[/tex]
Nessas condições, quanto vale [tex]f(13)+f(14)+f(15)[/tex]?
Solução
A Hydrangea macrophylla é uma planta com flor azul ou cor-de-rosa, dependendo do pH do solo no qual está plantada. Em solo ácido (ou seja, com [tex] pH \lt 7[/tex]) a flor é azul, enquanto que em solo alcalino (ou seja, com [tex] pH \gt 7[/tex]) a flor é rosa. Considere que a Hydrangea cor-de-rosa mais valorizada comercialmente numa determinada região seja aquela produzida em solo com pH inferior a [tex]8.[/tex]
Sabe-se que [tex]pH=–log_{10}x[/tex], em que [tex]x[/tex] é a concentração de íon hidrogênio ([tex]H^+[/tex]).
Para produzir a Hydrangea cor-de-rosa de maior valor comercial, deve-se preparar o solo de modo que [tex]x[/tex] assuma
(A) qualquer valor acima de [tex]10^{–8}.[/tex]
(B) qualquer valor positivo inferior a [tex]10^{–7}.[/tex]
(C) valores maiores que [tex]7[/tex] e menores que [tex]8.[/tex]
(D) valores maiores que [tex]70[/tex] e menores que [tex]80.[/tex]
(E) valores maiores que [tex]10^{–8}[/tex] e e menores que [tex]10^{–7}.[/tex]
III – Atividades em Grupo
O vídeo abaixo mostra como construir um sismógrafo simples.
COMO HACER UN SISMOGRAFO CASERO
(QUE FUNCIONA DE VERDAD)
Sismografo de Emil Wiechert
Para assistir, é só clicar na setinha.
Existem diversos componentes sofisticados que são utilizados nessa construção indicada no vídeo, o que pode dificultar para vocês a atividade.
Mas vocês podem pesquisar e encontrar um outro modo de construir um sismógrafo para cumprir a missão!
Vocês tomam cuidado com os ouvidos de vocês?
Leiam o texto a seguir e respondam as perguntas abaixo.
Observe a ilustração.
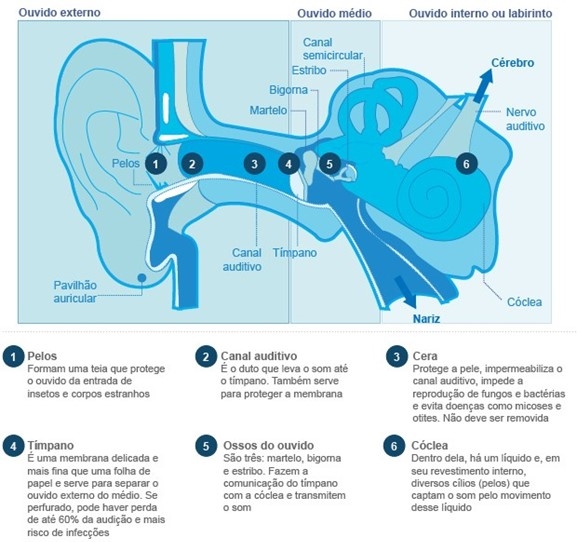
Quando o som está muito perto da orelha, ele é mais prejudicial porque vai direto para o tímpano.
Quando está propagado em um ambiente, como o interior de um carro, sofre interferência da janela, dos bancos e de toda a estrutura do automóvel até chegar ao tímpano, dessa vez com menor pressão sonora.
Assim como o resto do corpo, o ouvido também envelhece e, a partir dos 50 anos, as células auditivas começam a morrer. Esse envelhecimento, porém, não causa perda total da audição a não ser que esteja associado a outras doenças.
Fonte: Escutar som muito alto pode causar perda irreversível da audição (Acesso em 02/02/2024)
Pesquisem e enumerem tais fatores.
Pesquisem e enumerem tais fatores.
a) uma avenida;
b) um show de rock;
c) um cortador de grama;
d) uma turbina de avião;
e) um carro;
f) uma conversa.
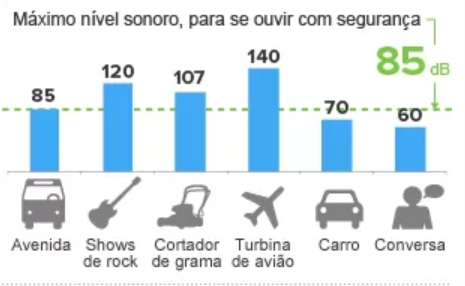
Imagem extraída do site G1 – Bem Estar. (Acesso em 02/02/2024.)
Qual seria essa expressão? Qual a unidade de medida para nível sonoro?
na qual
[tex]\quad N_S[/tex] é o nível sonoro;
[tex]\quad I[/tex] é a intensidade do som considerado;
[tex]\quad I_0[/tex] é o limiar de audibilidade.
● O nível sonoro é medido em decibéis [tex](dB). [/tex]
Pesquisem outras aplicações dos logaritmos e registrem a pesquisa de vocês em texto, imagens ou vídeo.
Se ficar bem bacana, poderemos postar no nosso Blog!
IV – Um vídeo para finalizar
Até agora vocês trabalharam com “fórmulas prontas” registradas nas discussões e nos problemas que apresentamos; pois, afinal, estávamos interessados na Matemática dos terremotos. Mas se vocês estão se perguntado como foram estabelecidas relações entre as várias grandezas que aparecem nessas fórmulas, assistam ao vídeo a seguir.
Vídeo do canal SerCiência – Tomás Silveira.
Equipe COM – OBMEP
