Problema
(Indicado a partir do 1º ano do E. M.)
Sejam [tex]x[/tex], [tex]y[/tex] e [tex]z[/tex] números reais que satisfazem as equações
[tex]\begin{cases}
log_{2}(xyz-3+log_{5}x)=5 \\
log_{3}(xyz-3+log_{5}y)=4 \\
log_{4}(xyz-3+log_{5}z)=4
\end{cases}[/tex] .
Sabendo que [tex]xyz[/tex] é um número inteiro, encontre o valor de [tex]|log_{5}x|+|log_{5}y|+|log_{5}z|[/tex].

Para ajudar. . .
Relações importantes no estudo de logaritmos:
Sendo [tex]b,b_1,\ldots, b_n[/tex] e [tex]a[/tex] números reais positivos, com [tex]a\neq1[/tex], temos que:
[tex]{\color{#800000}(1)} \, \, log_ab=c \iff b=a^c[/tex];
[tex]{\color{#800000}(2)} \, \, log_a b_1+log_a b_2+\ldots +log_a b_n=log_a(b_1b_2\cdots b_n)[/tex].
Propriedades da função dada por [tex]y=5^x[/tex]:
Sendo [tex]t[/tex] um número real, temos:
[tex]{\color{#800000}(3)} \, \, 5^t \gt 0[/tex].
[tex]{\color{#800000}(4)} \, \, 5^t \ge 1\Leftrightarrow t\ge 0 [/tex].
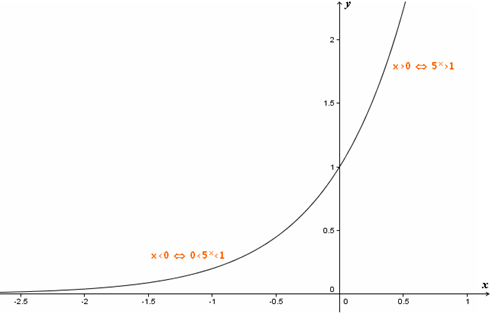
O gráfico da função [tex]f:\mathbb{R} \rightarrow ]0,+\infty[[/tex] dada por [tex] f(x)=5^x[/tex] pode ajudar a enxergar as propriedades [tex]{\color{#800000}(3)}[/tex] e [tex]{\color{#800000}(4)}[/tex].
Solução
Por [tex]{\color{#800000}(1)}[/tex], a primeira equação do sistema pode ser reescrita da seguinte forma:
[tex]\quad xyz-3+log_5{x}=2^5=32[/tex]. [tex]\qquad{\color{#800000}(i)}[/tex]
Analogamente, a segunda e a terceira se tornam:
[tex]\quad xyz-3+log_5{y}=81[/tex]; [tex]\qquad{\color{#800000}(ii)}[/tex]
[tex]\quad xyz-3+log_5{z}=256[/tex]. [tex]\qquad{\color{#800000}(iii)}[/tex]
Adicionando as três equações [tex]{\color{#800000}(i)}[/tex], [tex]{\color{#800000}(ii)}[/tex] e [tex]{\color{#800000}(iii)}[/tex] obtemos:
[tex]\quad 3xyz-9+log_5{x}+log_5{y}+log_5{z}=369[/tex],
donde, por [tex]{\color{#800000}(2)}[/tex],
[tex]\quad 3xyz+log_5{xyz}=378[/tex],
ou ainda
[tex]\quad log_5{xyz}=378-3xyz[/tex].
Por [tex]{\color{#800000}(1)}[/tex], esta última equação pode ser escrita como [tex] \, \boxed{5^{378-3xyz}=xyz}[/tex].
Dado que [tex]xyz[/tex] é um número inteiro, podemos afirmar que o lado direito da equação [tex] \, \boxed{5^{378-3xyz}=xyz} \, [/tex] será uma potência de [tex]5[/tex]. Podemos ir além: [tex]5^{378-3xyz}[/tex] não pode ser uma potência de [tex]5[/tex] maior do que [tex]125[/tex]. (Com efeito, por [tex]{\color{#800000}(3)}[/tex], [tex]xyz=5^{378-3xyz} \gt 0[/tex]; como [tex]xyz[/tex] é um número inteiro, então [tex]5^{378-3xyz}\ge 1[/tex], donde, por [tex]{\color{#800000}(4)}[/tex], [tex]378-3xyz \ge 0[/tex], ou seja, [tex]xyz \le 126[/tex].)
Assim, as possibilidades para [tex]xyz[/tex] são: [tex]5[/tex], [tex]25[/tex] e [tex]125[/tex]. Por verificação direta, observamos que [tex]xyz=125[/tex]; substituindo este valor em [tex]{\color{#800000}(i)}[/tex], [tex]{\color{#800000}(ii)}[/tex] e [tex]{\color{#800000}(iii)}[/tex], obtemos
[tex]\quad log_{5}x=-90[/tex];
[tex]\quad log_{5}y=-41[/tex];
[tex]\quad log_{5}z=134[/tex].
Finalmente, temos a soma [tex]\fcolorbox{black}{#eee0e5}{$|log_{5}x|+|log_{5}y|+|log_{5}z|=265$}[/tex] .
Solução elaborada pelos Moderadores do Blog.