Probabilidades
A ideia do acaso é quase tão antiga quanto as primeiras civilizações; entretanto, até pouco tempo, o acaso era visto como obra divina, sendo considerado como fenômeno natural (e, portanto, possível de ser estudado) só bem mais tarde. Conforme dito por Maurice George Kendall (estatístico britânico que viveu de 1907 a 1983):
- "A Humanidade precisou de centenas de anos para se acostumar com um mundo onde alguns eventos não tinham causa… ou eram determinados por causas tão remotas que somente podiam ser razoavelmente representados por modelos não-casuais."
Tendo isso em vista, não é difícil entender porque a "matematização" do acaso, do azar e do risco teve início há pouco mais de quinhentos anos! O estudo estruturado do acaso é uma das áreas mais recentes do conhecimento humano e atende pelos nomes Teoria das Probabilidades, ou Cálculo de Probabilidades ou simplesmente Probabilidade. Com ele temos ferramentas para modelarmos aquelas ações em que o "acaso" representa um papel preponderante e não podemos prever com certeza o que vai acontecer.
Nos dias de hoje, o raciocínio probabilístico aparece, mesmo que inconscientemente, em várias ações do nosso cotidiano: da decisão se levamos ou não um guarda-chuva quando saímos de casa à decisão de qual plano compramos para o nosso celular, estamos usando probabilidade. Isso sem enumerar as muitas situações, como as pesquisas que estão desenvolvidas para vacinas contra a COVID-19, que utilizam explicitamente ferramentas da Probabilidade. Enfim,
pintou incerteza, a Probabilidade está presente!
Muitos pesquisadores estão ativamente envolvidos na descoberta e estabelecimento de novas aplicações da Probabilidade nos campos da Medicina, Meteorologia, Fotografia de Satélites, Marketing, previsão de terremotos, comportamento humano, design de sistemas de computador, Finanças, Genética e Direito, só para exemplificar.
Nos currículos escolares, embora o estudo da Probabilidade se concentre mais fortemente no Ensino Médio, ele permeia o Ensino Fundamental dentro dos temas do Tratamento da Informação. Portanto,
não é por acaso que vamos estudar acasos nesta Sala…
E como surgiu a Probabilidade?
Particularmente, o estudo do acaso nasceu das tentativas de quantificação dos riscos dos seguros e de avaliar as chances de se ganhar em jogos de azar.
Além dos seguros das cargas transportadas durante as navegações, outros tipos de seguro influenciaram nas origens da Probabilidade. O seguro de vida, por exemplo, popularizou-se com o crescimento das cidades após a Idade Média, e é em torno desse tipo de seguro que surgiram os primeiros trabalhos matemáticos sobre esse tema. Em 1663, Edmond Halley (o mesmo do cometa) publicou o primeiro trabalho sobre seguro de vida, estimando o valor do prêmio do seguro em função da esperança de vida e da probabilidade de sobrevida. Por volta de 1730, a matemática dos seguros atinge um estado bastante maduro com os estudos do Matemático Daniel Bernoulli.

Imagem extraída da Wikiwand.
Os primeiros dados cúbicos que se tem notícias foram encontrados no Egito e datados de antes de 2000 AC e em escavações chinesas datadas de até 600 AC. Também os tetraedros foram encontrados em tumbas egípcias e os icosaedros eram usados na Grécia desde antes de Cristo. Na Índia, foram encontrados registros escritos de dados que datam de mais de dois mil anos.
Os povos Asiáticos e Mediterrâneos usavam em seus jogos o astrágalo, um ancestral do dado atual, formado por um osso de animal semelhante a um tetraedro irregular. Nele, as maiores faces eram numeradas por 3 e 4, enquanto as menores eram numeradas por 1 e 2.

Astrágalos
É também importante lembrar que antigamente jogava-se não só em apostas, mas também para prever o futuro, decidir disputas, dividir heranças, entre outros.
O desenvolvimento inicial do estudo da Probabilidade pode ser creditado às escolas italiana e francesa. Vejamos um pouco do que fez cada uma dessa escolas.
Os italianos dos séculos XV e XVI foram os pioneiros dos cálculos probabilísticos. Eles limitaram-se a resolver problemas concretos comparando, simplesmente, frequências de ocorrências e ganhos em jogos de azar, sem desenvolverem conceitos e teoremas.
► O frei Luca Pacioli (1445 – 1518) foi o primeiro autor conhecido a estudar jogos de azar. Ele chegou a analisar o famoso “problema dos pontos” que seria resolvido corretamente por Pascal e Fermat posteriormente. Escreveu em 1494 o trabalho Summa de arithmetica, geometria, proportioni e proportionalità ou simplesmente Summa.
► Niccolo Fontana (1499 – 1557), conhecido como Tartaglia, publicou sua obra General Trattato (1556) em que tratava dos problemas de Pacioli em algumas de suas páginas.
►Girolamo Cardano (1501 – 1576) foi o primeiro a introduzir técnicas de combinatória para calcular o número de casos favoráveis num evento e considerar a probabilidade como a razão entre o número de casos favoráveis e o número de casos possíveis. Dedicou-se principalmente a problemas envolvendo jogos de dados. Devido à sua fama na época, Cardano foi convidado para fazer o horóscopo de Eduardo VI. Prognosticou-lhe longa vida. O rei morreu no ano seguinte. Por outro lado, Cardano previu o dia exato de sua morte e acertou. Muitos dizem que cometeu suicídio para tornar realidade a sua previsão.
► Galileo Galilei (1564 – 1642) escreveu um breve artigo sobre os jogos de azar: Sopra le scoperta dei dadi (Sobre o jogo de dados), e presumiu que um dado tem probabilidade igual de cair em qualquer um dos seis lados.
Os franceses Blaise Pascal (1623-1662) e Pierre de Fermat (1601-1665) foram os pioneiros na resolução de problemas genéricos envolvendo probabilidades, mas nenhum deles chegou a tratar de teoremas envolvendo Probabilidade.
Para alguns historiadores e estudiosos, o cálculo de probabilidades se fortaleceu com os estudos feitos por Pascal ao tentar resolver o hoje conhecido como Problema dos Pontos. Como Pascal teria percebido que os métodos até então conhecidos eram insuficientes para que ele conseguisse resolver o problema, procurou ajuda de Fermat para discutir as suas ideias.
Acredita-se que foi esse problema que deu o início a uma troca de correspondências entre Pascal e Fermat no verão de 1654, na qual eles desenvolveram abordagens próprias e resolveram várias versões do problema. Pascal encontrou uma solução sistemática e generalizável que permite determinar a resposta a partir do famoso Triângulo de Pascal. (O Triângulo de Pascal está relacionado com os Coeficientes Binomiais e pode ser usado quando quisermos determinar o número de maneiras de selecionar um certo número de objetos de uma coleção.)
É só clicar no botão abaixo agora ou mais tarde!
Em torno de 1689, deixando de lado os seguros e os jogos de azar, Jakob Bernoulli (1654 – 1705) iniciou o processo de abstração das probabilidades com a publicação de um trabalho sobre séries no qual ele apresentou o resultado hoje conhecido como a “Lei dos Grandes Números” (vamos vê-la nesta Sala). No entanto, os principais resultados alcançados por Jakob Bernoulli foram publicados, em 1713, na obra Ars Conjectandi. A partir deste, dois trabalhos foram desenvolvidos: o Doctrine of Chance de Abraham de Moivre (1667 – 1754), em 1716, e o Laws of Chance de Thomas Simpson (1710 – 1761), em 1740.
No entanto, o maior marco da etapa clássica da Teoria das Probabilidades e considerado como a introdução definitiva do cálculo de probabilidades no mundo matemático foi publicado em 1812 por Pierre-Simon Laplace (1749 – 1827): o tratado Théorie Analytique des Probabilités .
A partir de então, os estudos clássicos de probabilidades continuaram e cresceram com o envolvimento de grandes matemáticos, como Johann Carl Friedrich Gauss, Leonhard Euler, o russo Andrei Andreyevich Markov (1856 – 1922), e os franceses Siméon Denis Poisson (1781 – 1840), Jules Henri Poincaré (1854 – 1912), Félix Édouard Justin Émile Borel (1871 – 1956), Henri Léon Lebesgue (1875 – 1941), Jean Le Rond d’Alembert (1717 – 1783), entre outros.
Em 1933, Andrey Nikolaevich Kolmogorov (1903 – 1987) iniciou a etapa moderna da Teoria das Probabilidades, apresentando uma axiomatização rigorosa e abstrata, baseada na Teoria dos Conjuntos.
Mas o que é mesmo Probabilidade?
Na Matemática é comum utilizarmos a palavra probabilidade com dois sentidos:
► Probabilidade como a área na qual encontramos ferramentas e técnicas para lidarmos com problemas da incerteza, do acaso. Nesse sentido, utilizamos a palavra probabilidade com o mesmo significado de Teoria das Probabilidades, teoria cujo objeto de estudo são os experimentos aleatórios – fenômenos que apresentam resultados imprevisíveis se repetidos várias vezes em processos semelhantes.
► Probabilidade como uma função que tem como objetivo medir a chance de um determinado evento ocorrer. Nesse sentido, perceba a importância dessa função: ela é tão especial que tem o mesmo nome da própria área de estudo na qual ela é definida!
Fora da Matemática, existe uma longa e interminável controvérsia em torno das diferentes interpretações do termo probabilidade, até porque, como tantos outros ramos da Matemática, o desenvolvimento da Teoria das Probabilidades tem sido estimulado pela variedade das suas aplicações. Mas a teoria matemática da Probabilidade não depende de interpretação e pode ser aplicada de maneira útil independentemente de em qual interpretação de probabilidade um problema particular está sendo analisado.
Particularmente, vamos apresentar matematicamente a função probabilidade e vamos explorá-la em três modelos diferentes da Teoria das Probabilidades. Mas, antes, vamos estabelecer ideias e noções gerais, que cabem como início dos estudos tanto da função probabilidade como nos três modelos que iremos explorar.
Conceitos básicos
Os chamados fenômenos ou experimentos aleatórios são processos reais ou hipotéticos nos quais os possíveis resultados podem ser identificados antecipadamente, mas não podemos prever com certeza o que vai acontecer: o "acaso" representa um papel preponderante. Assim, um experimento aleatório possui duas características fundamentais:
– O resultado não pode ser previsto com certeza.
– Embora não seja possível afirmar que resultado em particular ocorrerá, é possível descrever o conjunto de todos os resultados possíveis do experimento.
São exemplos de experimentos aleatórios:
(2) Escolher uma peça de um lote de fabricação e verificar se a mesma tem ou não defeito.
(3) A cobrança de um pênalti por um jogador de futebol.
(4) O lançamento de uma moeda e a verificação se, depois da queda, a face voltada para cima é cara ou coroa.
(5) A retirada de uma bola de uma urna com [tex]50[/tex] bolas numeradas de [tex]1[/tex] a [tex]50[/tex] e observação de seu número.
(6) Verificar o tipo sanguíneo de um habitante de uma cidade escolhido ao acaso.
(7) Retirar uma carta de um baralho completo e verificar o seu naipe.
Mesmo apresentando resultados imprevisíveis se repetidos várias vezes em processos semelhantes, podemos quantificar a chance que cada resultado possível tem de ocorrer em fenômenos aleatórios utilizando ferramentas da Teoria das Probabilidades. Para facilitar a apresentação dessas ferramentas, é usual denominar o conjunto de todos os possíveis resultados de um experimento aleatório de espaço amostral do experimento e de eventos os possíveis resultados de um experimento.
Cada elemento de um espaço amostral é denominado ponto amostral.
► Evento: qualquer subconjunto do espaço amostral. Os eventos geralmente são indicados por letras maiúsculas do nosso alfabeto, indexadas ou não; e, na prática, dizemos que um evento E ocorre se, quando realizado o experimento, obtém-se um resultado que pertence a E.
Um primeiro passo no estudo de um experimento aleatório é compreendermos os resultados possíveis de se obter com a realização desse experimento, ou seja, antes de mais nada, é necessário conhecer e entender bem o espaço amostral do experimento.
► Para os experimentos exemplificados acima, observe que os respectivos espaços amostrais são os seguintes:
(2) [tex]\Omega_2 = \{[/tex]peça defeituosa , peça sem defeitos[tex]\}[/tex].
(3) [tex]\Omega_3 = \{[/tex]pênalti convertido , pênalti desperdiçado[tex]\}[/tex] ou
[tex]\quad \;\,\Omega_3 = \{[/tex]pênalti convertido , defesa do goleiro , bola chutada para fora[tex]\}[/tex],
dependendo do que desejamos analisar.
(4) [tex]\Omega_4=\{[/tex]cara , coroa[tex]\}[/tex].
(5) [tex]\Omega_5=\{1,2,3,4,\cdots,49,50\}[/tex].
(6) [tex]\Omega_6=\{A, B, AB, O\}[/tex].
(7) [tex]\Omega_7=\{[/tex]ouros, copas, paus, espadas[tex]\}[/tex].
► Para esses experimentos, podemos, por exemplo, definir respectivamente os seguintes eventos:
(2) [tex]E_2:[/tex] A peça escolhida é defeituosa. Neste caso, [tex]E_2=\{[/tex]peça defeituosa [tex]\}\subset \Omega_2[/tex].
(3) [tex]E_3:[/tex] O jogador fez o gol. Neste caso, [tex]E_3= \{[/tex]pênalti convertido[tex]\}\subset \Omega_3[/tex].
(4) [tex]E_4:[/tex] Obter cara. Neste caso, [tex]E_4=\{[/tex]cara[tex]\}\subset \Omega_4[/tex].
(5) [tex]E_5:[/tex] Retirar uma bola com numeração acima de [tex]45[/tex]. Neste caso, [tex]E_5=\{46,47,48,49,50\}\subset \Omega_5[/tex].
(6) [tex]E_6:[/tex] O tipo sanguíneo do habitante é [tex]AB[/tex]. Neste caso, [tex]E_6=\{AB\}\subset \Omega_6[/tex].
(7) [tex]E_7:[/tex] O naipe da carta é paus. Neste caso, [tex]E_7=\{[/tex]paus[tex]\}\subset \Omega_7[/tex].
Observação: Em geral, um evento é definido por uma sentença, como fizemos nos sete exemplos anteriores.
Tipos especiais de eventos
► Há eventos que sempre ocorrem e por isso são chamados de eventos certos. Já os que nunca ocorrem são chamados de eventos impossíveis.
Lançar um dado, cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex], e "obter um número menor do que oito" é um evento certo; mas "obter um número maior do que dez" é um evento impossível.
► Dentro de um mesmo espaço amostral, quando a ocorrência de um evento impossibilita a ocorrência de outro evento dizemos que os eventos são mutuamente excludentes ou disjuntos.
No lançamento de um dado com as faces numeradas de [tex]1[/tex] a [tex]6[/tex], por exemplo, os eventos "obter um valor maior do que quatro" e "obter um valor menor do que 2" são mutuamente excludentes, já que os dois não podem ocorrer simultaneamente.
► Os eventos que possuem apenas um resultado do experimento são chamados de eventos elementares ou eventos simples; esses eventos são os subconjuntos unitários do espaço amostral. Assim, cada evento elementar é formado por um único ponto amostral.
Os eventos [tex]E_2[/tex], [tex]E_3[/tex], [tex]E_4[/tex], [tex]E_6[/tex] e [tex]E_7[/tex] dos nossos exemplos de experimentos são todos elementares. No lançamento de um dado, cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex], temos seis eventos elementares: [tex]\{1\}[/tex], [tex]\{2\}[/tex], [tex]\{3\}[/tex], [tex]\{4\}[/tex], [tex]\{5\}[/tex] e [tex]\{6\}[/tex]. No Sorteio da Mega-Sena, cada cartão com seis números que pode ser apostado é um exemplo de um evento elementar.
Observe que, como os eventos são conjuntos, podemos definir operações entre eles.
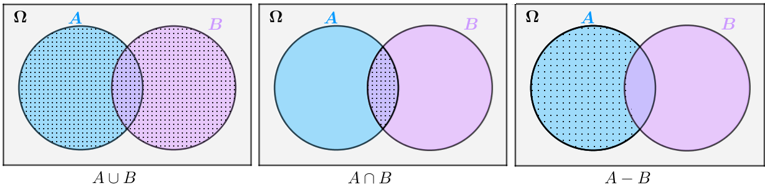
Dessa forma, dados dois eventos podemos utilizar operações entre conjuntos de modo a criar novos eventos, como mostramos abaixo.
Composição de eventos
Sejam [tex]A[/tex] e [tex]B[/tex] eventos de um mesmo experimento aleatório.
► O conjunto [tex]A \cup B\;[/tex] indica um evento que ocorre se e somente se pelo menos um dos dois eventos, [tex]A[/tex] ou [tex]B[/tex], ocorre.
► O conjunto [tex]A \cap B\;[/tex] indica um evento que ocorre se e somente se os dois eventos, [tex]A[/tex] e [tex]B[/tex], ocorrem simultaneamente.
– Usando essa simbologia, podemos dizer que os eventos [tex]A[/tex] e [tex]B[/tex] são mutuamente excludentes quando [tex]A \cap B=\emptyset [/tex].
► O conjunto [tex]A-B\;[/tex] indica um evento que ocorre se e somente se [tex]A[/tex] ocorre, mas [tex]B[/tex] não ocorre.
► O evento complementar de um evento [tex]A[/tex], que indicamos por [tex]\overline{A}[/tex] ou [tex]A^C[/tex], é o conjunto formado por todos os resultados do experimento que não pertencem a [tex]A[/tex]. Assim, [tex]\overline{A}[/tex] ocorre se e somente se [tex]A[/tex] não ocorre.
Se [tex]A_1,A_2,\cdots,A_n[/tex] são eventos de um mesmo experimento aleatório, podemos generalizar as duas combinações iniciais de eventos.
► A união [tex]A_1\cup A_2\cup \cdots \cup A_n\;[/tex], que pode ser simbolizada por [tex] {\textstyle \bigcup\limits_{i=1}^n} A_i[/tex], indica um evento que ocorre quando pelo menos um dentre os eventos [tex]A_1,A_2,\cdots,A_n[/tex] ocorrer.
► A interseção [tex]A_1\cap A_2\cap \cdots \cap A_n\;[/tex], que pode ser simbolizada por [tex] {\textstyle \bigcap\limits_{i=1}^n} A_i[/tex], indica um evento que ocorre quando todos os eventos [tex]A_1,A_2,\cdots,A_n[/tex] ocorrerem.
A seguir, vamos ver alguns exemplos de eventos definidos a partir de outros eventos:
[tex]\qquad \qquad A_1[/tex]: "o número escolhido é ímpar";
[tex]\qquad \qquad A_2[/tex]: "o número escolhido é primo".
Assim, [tex]A_1=\{1,3,5,7\}\,[/tex], [tex]A_2=\{2,3,5,7\}\,[/tex] e, utilizando as operações entre conjuntos, podemos nos referir aos seguintes eventos:
[tex]\qquad \qquad A_1 \cup A_2[/tex]: "o número escolhido é ímpar ou primo", ou seja, [tex]A_1 \cup A_2 = \{1, 2, 3 , 5,7\}[/tex].
[tex]\qquad \qquad A_1 \cap A_2[/tex]: "o número escolhido é ímpar e primo", ou seja, [tex]A_1 \cap A_2 = \{3 , 5, 7\}[/tex].
Para esse evento, podemos definir a seguinte sequência de eventos para qualquer [tex]i\in \{1,2,3,4,5\}[/tex]:
[tex]\qquad \qquad A_i:[/tex] ocorrência de um número maior do que [tex]2i[/tex].
Assim:
[tex]\qquad A_1=\{3,4,5, \cdots,200\}[/tex];
[tex]\qquad A_2=\{5,6,7,\cdots,200\}[/tex];
[tex]\qquad A_3=\{7,8,9,\cdots,200\}[/tex];
[tex]\qquad A_4=\{9,10,11,\cdots,200\}[/tex];
[tex]\qquad A_5=\{11,12,13,\cdots,200\}[/tex];
[tex]\qquad {\textstyle \bigcup\limits_{i=1}^5} A_i=\{3,4,5, \cdots,200\}[/tex];
[tex]\qquad {\textstyle \bigcap\limits_{i=1}^5} A_i=\{11,12,13, \cdots,200\}[/tex].
Espaço Amostral:
[tex]\qquad \Omega_4 = \{cara , coroa\}[/tex]
É possível definir os seguintes eventos para este experimento:
[tex]\qquad E_1 = \emptyset[/tex]
[tex]\qquad E_2 = \{cara\}[/tex]
[tex]\qquad E_3 = \{coroa\}[/tex]
[tex]\qquad E_4 = \{cara, coroa\}[/tex]
Algumas considerações:
[tex]\textcolor{#8b4513}{(i)}[/tex] Podemos garantir que listamos todos os eventos do experimento, já que um conjunto com [tex]n[/tex] elementos possui [tex]2^n[/tex] subconjuntos.
[tex]\textcolor{#8b4513}{(ii)}[/tex] Os eventos [tex]E_2[/tex] e [tex]E_3[/tex] são disjuntos e um é o complementar do outro.
[tex]\textcolor{#8b4513}{(iii)}[/tex] O evento [tex]E_1[/tex] por não possuir elemento é dito evento impossível.
[tex]\textcolor{#8b4513}{(iv)}[/tex] O evento [tex]E_4[/tex] é o próprio espaço amostral e por isso é um evento certo.
Espaço amostral:
Aqui, podemos definir os seguintes Eventos:
[tex]\qquad \Omega_1 = \{1 , 2 , 3 , 4 , 5 , 6\}[/tex]
[tex]\qquad[/tex] Evento [tex]A[/tex]: "o resultado foi par" , ou seja, [tex]A = \{2 , 4 , 6\}[/tex].
[tex]\qquad[/tex] Evento [tex]B[/tex]: "o resultado foi ímpar", ou seja, [tex]B = \{1 , 3 , 5\}[/tex].
[tex]\qquad[/tex] Evento [tex]C[/tex]: "o resultado foi maior do que 4", ou seja, [tex]C = \{5 , 6\}[/tex].
[tex]\qquad[/tex] Evento [tex]D[/tex]: "o resultado foi par ou maior do que 4", ou seja, [tex]D = A \cup C= \{2 , 4 , 5 , 6\}[/tex].
[tex]\qquad[/tex] Evento [tex]E[/tex]: "o resultado foi par e maior do que 4", ou seja, [tex]E = A \cap C = \{6\}[/tex].
Algumas considerações:
[tex]\textcolor{#8b4513}{(i)}[/tex] Listamos apenas alguns dos [tex]2^6 = 64[/tex] eventos existentes.
[tex]\textcolor{#8b4513}{(ii)}[/tex] O evento [tex]B[/tex] é o complementar de [tex]A[/tex], pois [tex]\Omega_1 – A = B[/tex].
[tex]\textcolor{#8b4513}{(iii)}[/tex] O evento [tex]A[/tex] é o complementar de [tex]B[/tex], pois [tex]\Omega_1 – B = A[/tex].
[tex]\textcolor{#8b4513}{(iv)}[/tex] Os eventos [tex]A[/tex] e [tex]B[/tex] são mutuamente excludentes, pois [tex]A \cap B = \emptyset[/tex].
[tex]\textcolor{#8b4513}{(v)}[/tex] O evento [tex]E[/tex] é um evento elementar, pois possui apenas [tex]6[/tex] como elemento.
Além dos fenômenos aleatórios, existem os fenômenos determinísticos: aqueles que repetidos sob as mesmas condições conduzem ao mesmo resultado. Embora não iremos tratar desse tipo de fenômeno nesta Sala, vejam alguns exemplos de fenômenos determinísticos: a temperatura de ebulição da água sob as mesmas condições físicas; o tempo que um carro numa velocidade média de [tex]80 \text{ km/h}[/tex] levará para percorrer um trajeto de [tex]300 \text{ km}[/tex]; um corpo colocado a [tex]50 \text{ m}[/tex] de altura e depois solto, cai por ação da gravidade; as Leis da Física e da Química (Lei de Ohm, Lei de Kepler, etc.); medição de objetos; as técnicas de cálculo.
Observem que é possível observar um mesmo experimento sob o aspecto da aleatoriedade e do determinismo. Perceba que, no experimento de soltar uma pena de uma certa altura, temos o evento determinístico de que a pena atingirá o chão e o evento aleatório que é a posição que a pena assumirá quando atingir o solo.
Feitas essas observações, que tal vocês fazerem algumas atividades?
– É só clicar no botão a seguir e
Bons estudos!!!
A chance de um evento ocorrer
Ao analisarmos experimentos aleatórios, é bastante conveniente dispormos de uma medida que quantifique a incerteza presente em cada experimento analisado, já que perceber o comportamento de eventos relacionados a fenômenos aleatórios e entender quais são as chances reais de eles ocorrerem é de grande importância para a nossa sociedade. E, embora não exista uma maneira única de quantificarmos a chance de um evento ocorrer, independentemente de como associemos números a eventos, a teoria matemática funciona.
Assim, nos nossos estudos, vamos apresentar inicialmente a definição axiomática da Função Probabilidade e vamos explorar essa definição em três modelos diferentes da Teoria das Probabilidades: a Probabilidade Clássica; a Probabilidade Frequencial e a Probabilidade Condicional (existem outras, viu?).
Dividimos a nossa discussão em quatro Salas praticamente independentes, mas sugerimos fortemente que elas sejam acessadas na ordem na qual estão apresentadas. No canto inferior direito de cada uma delas, vocês encontrarão um link para voltarem para esta Sala e, se for necessário, fazer uma nova escolha. As salas abrirão em janelas diferentes do navegador de vocês.
Antes de vocês percorrerem as nossas Salas, talvez seja conveniente lembrar que uma mesma palavra pode ter vários significados. Particularmente em nossas Salas utilizamos a palavra chance com o significado que encontramos em um dicionário da língua portuguesa, ou seja, como a "possibilidade de algo acontecer", como podemos ver, por exemplo, clicando AQUI. Fazemos esta observação, pois em Estatística a palavra chance pode ser definida como a razão entre a probabilidade de um evento ocorrer e a probabilidade do evento não ocorrer, isto é, [tex] \dfrac{p} {1-p}[/tex], com [tex]p[/tex] sendo a probabilidade de o evento em questão ocorrer. Assim, poderíamos dizer que, neste caso, a chance seria a razão do esperado pelo inesperado!
➤ Sala 2: Probabilidade Clássica.
➤ Sala 3: Probabilidade Condicional.
➤ Sala 4: Probabilidade Frequencial.
Vamos lá?
| Sala 1 | Sala 2 | Sala 3 | Sala 4 |
Equipe COM – OBMEP
Janeiro de 2021.
[01] Algumas considerações sobre a origem da Teoria da Probabilidade (Último acesso em 17/12/20)
[02] Aulete Digital (Último acesso em 17/12/20)
[03] A Matemática do Ensino Médio, volume 2: Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[04] Análise Combinatória e Probabilidade: Coleção do Professor de Matemática – Augusto César Morgado; João Bosco Pitombeira de Carvalho; Paulo Cesar Pinto Carvalho e Pedro Fernandez.
[05] Enciclopédia Britânica (Último acesso em 17/12/20)
[06] Fundamentos de Matemática Elementar, volume 5 – Samuel Hazzan.
[07] GeoGebra (Último acesso em 17/12/20)
[08] Início da matematização das probabilidades (Último acesso em 17/12/20)
[09] Introdução à Teoria das Probabilidades – Prof. Victor Hugo Lachos Davila. (Último acesso em 17/12/20)
[10] Probabilidade – Profa. Ana Maria Lima de Farias; Prof. Luiz da Costa Laurencel. (Último acesso em 17/12/20)
[11] Probability and Statistics – Morris H. Degroot; Mark J. Schervish.
[12] MacTutor – Várias páginas (Último acesso em 17/12/20)
[13] Matemática, volume único – Gelson Iezzi; Osvaldo Dolce; David Mauro Degenszajn; Roberto Périgo.
[14] Wikiwand (Último acesso em 17/12/20)
[15] Wikipedia (Último acesso em 17/12/20)
[16] YouTube (Último acesso em 17/12/20)
