Atividade: Proporção em Geometria


Para executar alguns recursos desta sala, você precisa ter o plug-in Adobe Flash Player instalado no dispositivo que você está utilizando.


Proporção em Geometria
 

Tópicos

I – Apresentação do Tema

carinha19

Pessoal . . .
Vocês ficaram sabendo desta notícia?

 

Há aranhas gigantes à solta em Lisboa

aranha

Aranhas gigantescas apareceram, do nada, na Ponte 25 de Abril, em Lisboa – Portugal, e estão aterrorizando motoristas. A espécie é desconhecida dos especialistas e o motivo que as levou a invadirem a ponte, também.
As autoridades acalmam a população e afirmam que não há motivos para pânico…
Vejam imagens desse ataque de aranhas gigantes na reportagem mostrada neste vídeo.

v7

Nossa !!!!!!!!!
É apavorante, não é?

 carinha19

É apavorante para quem não sabe Proporção e Geometria . . .

 

Agora, além de apavorado, fiquei confuso…

 

 Desafio2

Recomendo, então, que você fique atento à discussão que faremos aqui, pois o tema desta Sala de Atividades é
Proporção em Geometria!

 

A proporcionalidade é um dos conceitos da matemática mais presentes no dia a dia de cada um de nós. Por exemplo, para encontrar proporcionalidade, basta olhar para algo que nos acompanha a cada instante: a nossa sombra.
Mesmo dentro da própria Matemática não é raro a proporcionalidade aparecer na aritmética, na geometria e na álgebra, já que ela depende de noções muito simples de quocientes e de igualdades.
Aqui trataremos de situações nas quais a proporcionalidade invade a geometria, já que nos ocuparemos de relações entre figuras geométricas que, de alguma forma, serão divididas em iguais proporções.
Essa parceria Proporção e Geometria, além de bela, é antiga, existe há mais de 2500 anos! Foi utilizando noções simples de semelhança e proporcionalidade que, por exemplo, sábios da Antiguidade encontrarem métodos de calcular os tamanhos da Terra, do Sol e da Lua.
Na nossa discussão não mediremos especificamente tamanhos e distâncias entre astros, mas apresentaremos cinco temas centrais da Geometria Plana que podem ser utilizados não somente nesse tipo de medição mas também no combate a criaturas colossais…

E aí, dispostos a decifrarem o mistério das aranhas gigantes?
Então, muita calma, a todos, e boa diversão!!!

II – O Teorema de Tales e aplicações

Iniciaremos a nossa discussão com um resultado cuja descoberta é atribuída a Tales de Mileto, um dos sete sábios da Grécia, que viveu no século VI a.C.: o Teorema de Tales.
Esse é um dos teoremas centrais da geometria plana e tem um papel fundamental na teoria da semelhança e na trigonometria, o que lhe rende inúmeras aplicações práticas. Portanto, se vocês não conhecem este teorema, sigam estes três passos:

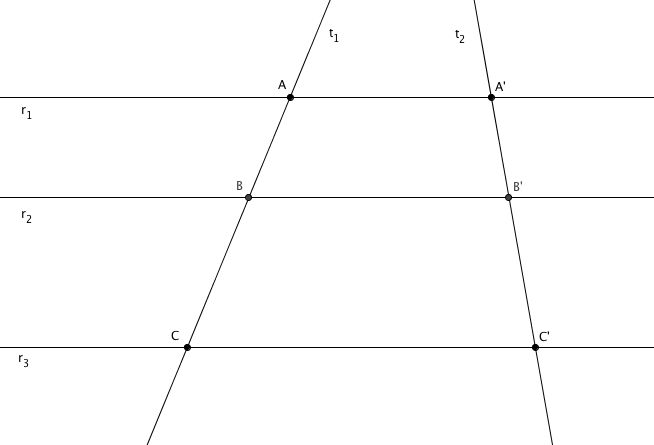
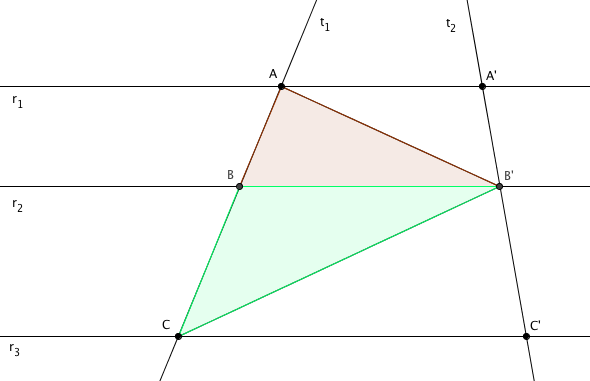
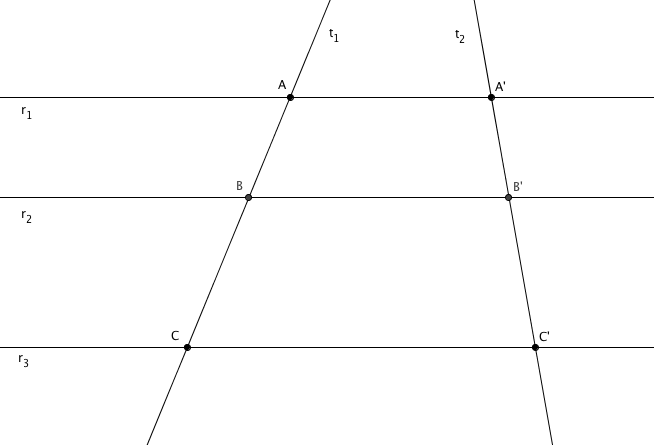
  • A primeira coisa a fazer é pegar papel e lápis, ler com bastante atenção o enunciado, fazer uma boa figura com três retas paralelas e duas transversais a elas e tentar entender o que o teorema está garantindo.
  • Em seguida, utilizem este applet para visualizar o resultado garantido pelo Teorema: façam várias simulações, até vocês se convencerem de que parece que Tales tinha razão…
  • Finalmente, leiam com cuidado a prova do teorema e comprovem que Tales realmente tinha razão!

O Teorema de Tales

Se um feixe de retas paralelas, com no mínimo três retas, é intersectado por duas retas transversais, então dois segmentos quaisquer de uma das transversais são proporcionais aos segmentos correspondentes da outra.

Sejam [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex] retas paralelas e [tex]t_1[/tex] e [tex]t_2[/tex] as transversais, conforme mostra a figura a seguir.
Teorema de Tales

Queremos mostrar que [tex]\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}[/tex], sendo que [tex]AB, \, BC, \, A’B’, \, B’C'[/tex] denotam, respectivamente, os comprimentos dos segmentos [tex]\overline{AB}, \, \overline{BC}, \, \overline{A’B’}, \, \overline{B’C’}[/tex].

Como [tex]r_1//r_2[/tex], então as distâncias de [tex]A[/tex] a [tex]r_2[/tex] e de [tex]A'[/tex] a [tex]r_2[/tex] são iguais, ou seja, [tex]d(A, r_2) = d(A’,r_2)[/tex].
Assim, como os triângulos [tex]ABB'[/tex] e [tex]A’BB'[/tex] possuem mesma altura em relação à base comum [tex]BB'[/tex], concluímos que esses dois triângulos têm a mesma área.
Denotaremos esse fato por [tex]S(ABB’) = S(A’BB’)[/tex][tex] \, \, \, (I)[/tex].

Teorema de Tales 2

De modo análogo, conclui-se que os triângulos [tex]B’BC[/tex] e [tex]BB’C'[/tex] tem a mesma área, isto é, [tex]S(B’BC) = S(BB’C’)[/tex][tex] \, \, \, (II)[/tex].

Perceba também que a distância do ponto [tex]B'[/tex] à reta [tex]t_1[/tex] é a altura dos triângulos [tex]ABB'[/tex] e [tex]B’BC[/tex] relativa aos lados [tex]AB[/tex] e [tex]BC[/tex] respectivamente; deste modo temos que:
[tex]\qquad \quad \dfrac{S(ABB’)}{S(B’BC)} =\dfrac{\dfrac{AB\times altura}{2}}{\dfrac{BC\times altura}{2}}= \dfrac{AB}{BC}[/tex],
ou ainda,
[tex\qquad \quad \dfrac{S(ABB’)}{S(B’BC)} =\dfrac{AB}{BC}[/tex][tex] \, \, \, (III)[/tex].
Teorema de Tales
De modo análogo, [tex]\dfrac{S(A’BB’)}{S(BB’C’)} = \dfrac{A’B’}{B’C’}[/tex][tex] \, \, \, (IV)[/tex].

Agora, dividindo membro a membro [tex](I)[/tex] e [tex](II)[/tex] temos [tex]\dfrac{S(ABB’)}{S(B’BC)} = \dfrac{S(A’BB’)}{S(BB’C’)}[/tex][tex] \, \, \, (V)[/tex].

Também, de [tex](III)[/tex], [tex](IV)[/tex] e [tex](V)[/tex], temos [tex]\dfrac{AB}{BC} = \dfrac{A’B’}{B’C’}[/tex][tex] \, \, \, (VI)[/tex].

Finalmente, multiplicando ambos os membros de [tex](VI)[/tex] por [tex]\dfrac{BC}{A’B’}[/tex] temos [tex]\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}[/tex].

Agora que vocês já entenderam o Teorema de Tales, que tal conhecerem algumas de suas aplicações?
Então, cliquem no botão abaixo. Vamos lá, pessoal!

As duas investigações e os três problemas indicados abaixo são aplicações do Teorema de Tales.

Resolvam os seguintes problemas:

1) Três lotes são limitados pelas ruas A e B, sendo suas cercas laterais perpendiculares à rua A, conforme a figura a seguir.
Teorema de Tales (1)

Determinem a medida de comprimento da frente de cada terreno para a rua B.

2) (Teorema da Bissetriz Interna) A bissetriz de um ângulo interno de um triângulo divide o lado oposto a esse ângulo em dois segmentos proporcionais aos seus lados adjacentes.
Provem esse resultado utilizando o Teorema de Tales.

3) Na prova do Teorema de Tales, tomamos dois segmentos consecutivos [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex] na transversal [tex]t_1[/tex].
Mostrem que o resultado continua válido para segmentos não consecutivos.

 

Realizem as seguintes investigações:

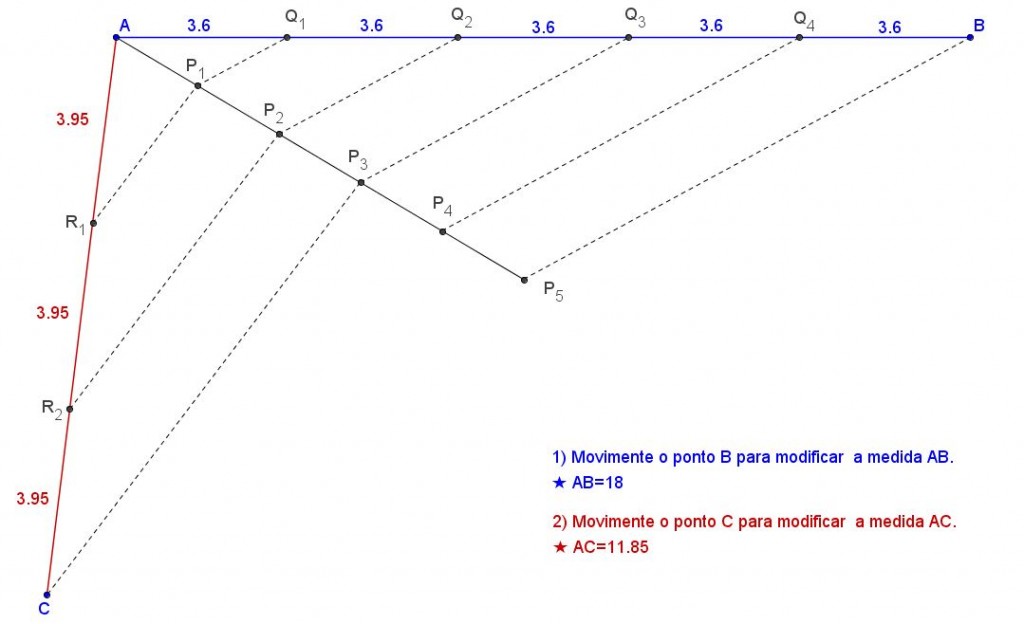
1) Como efetuar a divisão de um segmento em partes congruentes, usando apenas régua não graduada e compasso.

2) Como dividir a região limitada por um triângulo em n regiões de mesma área, usando apenas régua não graduada e compasso.

Se vocês estão com dificuldades para realizarem a divisão de um segmento em partes congruentes, utilizem este applet, talvez ele possa ajudá-los na determinação de um procedimento geral.

Divisão de segmentos em partes congruentes

Com esse applet é possível dividir dois segmentos, [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] em, respectivamente, cinco e três partes congruentes.
Para facilitar o manuseio e ampliar a área de trabalho, o applet abrirá em uma outra janela.
Para utilizar o applet, basta clicar na figura abaixo!

divisao

III – Semelhança de Triângulos e aplicações

Dentre os polígonos, o triângulo é considerado o mais simples, já que é definido com o menor número de lados – apenas 3. Mas, apesar de sua aparente simplicidade, são muitas as situações em que se recorre a outra característica do triângulo – a sua estabilidade. Afinal três pontos não colineares definem um, e somente um, plano.
Na construção civil, por exemplo, são muitas as soluções de questões relacionadas à segurança de estruturas que se apoiam na simplicidade e na robustez do triângulo.
E é no estudo dos triângulos que encontraremos mais um exemplo da Proporcionalidade na Geometria.

Triângulos semelhantes

Vamos relembrar o que são triângulos semelhantes?

Definição:
Dois triângulos são ditos semelhantes quando existe uma correspondência biunívoca entre seus vértices, de modo que
(i) ângulos internos correspondentes são congruentes;
(ii) lados correspondentes são proporcionais.

Na figura abaixo, os triângulos [tex]ABC[/tex] e [tex]DEF[/tex] com a seguinte correspondência entre vértices:

[tex]A\longleftrightarrow D\qquad \quad [/tex] [tex]B\longleftrightarrow E\qquad \quad [/tex] [tex]C\longleftrightarrow F[/tex]

são semelhantes.

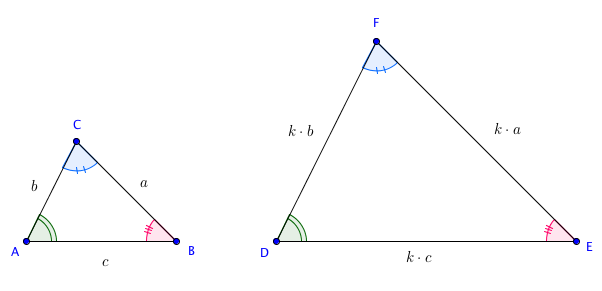
Semelhança

Como os dois triângulos são semelhantes, podemos afirmar que:

  • [tex]\widehat{A}[/tex] e [tex]\widehat{D}[/tex] são ângulos congruentes, isto é, ângulos com a mesma medida.
  • [tex]\widehat{B}[/tex] e [tex]\widehat{E}[/tex] são ângulos congruentes.
  • [tex]\widehat{C}[/tex] e [tex]\widehat{F}[/tex] são ângulos congruentes.
  • Os lados correspondentes são proporcionais, isto é, existe um número real positivo [tex]k[/tex], tal que:
    [tex]\qquad \quad \dfrac{DE}{AB}=\dfrac{EF}{BC}=\dfrac{FD}{CA}=k[/tex].

Observem quantas informações importantes no estudo da geometria vocês conseguem obter, sabendo que dois dados triângulos são semelhantes. São três igualdades de medidas de ângulos e três proporcionalidades de comprimentos de segmentos.

O que sabemos até agora sobre semelhança de triângulos?

– Por um lado, sabendo que dois dados triângulos são semelhantes, obtemos três igualdades e três proporcionalidades.
– Mas por outro, é necessário termos em mãos doze medidas para verificarmos se dois dados triângulos são semelhantes:

  • as medidas dos três ângulos internos do primeiro triângulo;
  • as medidas dos três lados do primeiro triângulo;
  • as medidas dos três ângulos internos do segundo triângulo;
  • as medidas dos três lados do segundo triângulo.

Assim, precisamos de outras informações sobre semelhança de triângulos, além da única temos: a definição. Apresentaremos, então, algumas propriedades que nos permitirão concluir que dois triângulos são semelhantes, a partir de um número menor de medidas conhecidas. Vejamos.

Casos de semelhança de triângulos

As três propriedades conhecidas como casos (ou critérios) de semelhança são, na verdade, condições mínimas que, se verificadas, nos permitem afirmar que dois triângulos são semelhantes. Com certeza você se lembra delas, não é?

Caso A.A. (ângulo – ângulo):
Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.

Caso L.A.L. (lado – ângulo – lado):
Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e os ângulos internos definidos por esses lados são congruentes, então os triângulos são semelhantes.

Caso L.L.L. (lado – lado – lado):
Se os três lados de um triângulo são proporcionais aos três lados de outro triângulo, então os triângulos são semelhantes.

A próxima propriedade é também um resultado clássico da Geometria Plana e mostrará uma situação muito especial na qual dois triângulos serão sempre semelhantes.

Teorema Fundamental da Proporcionalidade

Teorema:
Se uma reta paralela a um dos lados de um triângulo intersecta os outros dois lados em pontos distintos, então ela determina um triângulo semelhante ao triângulo inicial.

Observem a próxima figura.

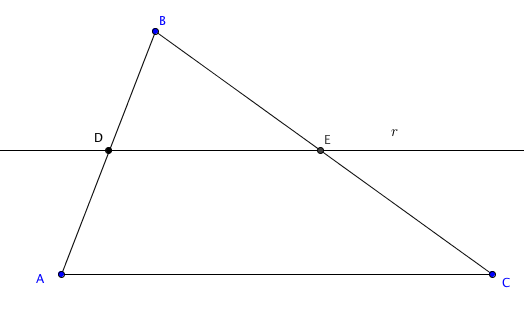
Proposição

Se a reta [tex]r[/tex], determinada pelos pontos [tex]D[/tex] e [tex]E[/tex], for paralela ao lado [tex]AC[/tex], então os triângulos [tex]ABC[/tex] e [tex]DBE[/tex] são semelhantes. Neste caso, a correspondência entre vértices será:

[tex]A\longleftrightarrow D\qquad \quad [/tex] [tex]B\longleftrightarrow B\qquad \quad [/tex] [tex]C\longleftrightarrow E[/tex]

As demonstrações desses quatro resultados não serão discutidas nesta sala, pois fogem do foco da nossa discussão. Dessa forma, nas atividades que apresentaremos a seguir, vocês poderão utilizar livremente as quatro propriedades apresentadas para concluir, quando necessário, que dois dados triângulos são semelhantes.

Aplicações da semelhança de triângulos

Proporemos, agora, problemas teóricos e práticos que podem ser solucionados com a teoria que apresentamos neste tópico. Em alguns desses problemas, vocês poderão observar como a Semelhança de Triângulos é importante no trabalho de topógrafos, cartógrafos e engenheiros, principalmente quando houver necessidade de se obter distâncias inacessíveis por serem muito longas ou com algum tipo de obstáculo. Nessas situações, esses profissionais têm que trabalhar com medidas de ângulos e, para obtê-las, eles muitas vezes utilizam um instrumento chamado teodolito. Se você não sabe o que é um teodolito, clique no botão abaixo, antes de prosseguir.

O teodolito é um instrumento ótico utilizado para medir ângulos, tanto horizontais como verticais, em medidas diretas e indiretas de distâncias.
teodolito2 Por agora, vocês só precisam saber que podemos, particularmente, utilizar um teodolito com a mesma finalidade que vocês utilizam os seus transferidores.transfPara saber mais sobre este instrumento, cliquem aqui e conheçam a página do Teodolito, na seção de Instrumentos Científicos, do Museu de Astronomia e Ciências Afins – MAST.

Vamos, então, aos problemas. Bons estudos!

Resolvam e justifiquem as soluções dos problemas a seguir. Ao utilizarem uma das quatro propriedades enunciadas neste tópico, citem-na.
1) Considere o triângulo retângulo ABC mostrado na figura, em que AH é a altura relativa à sua hipotenusa.
Utilize semelhança de triângulos para provar as seguintes relações:
Relações Métricas
a) [tex]h^2 = m \cdot n[/tex];

b) [tex]b^2 = a \cdot m[/tex];

c) [tex]c^2 = a \cdot n[/tex];

d) [tex]b^2 + c^2 = a^2[/tex];

e) [tex]b \cdot c = a \cdot h[/tex];

f) [tex]\dfrac{1}{h^2} = \dfrac{1}{b^2} + \dfrac{1}{c^2}[/tex].

2) Um engenheiro querendo medir a distância entre dois pontos [tex]C[/tex] e [tex]D[/tex] na margem de um lago, utilizou um teodolito de modo a marcar [tex]\overline{AB}[/tex] paralelo a [tex]\overline{CD}[/tex].
Tendo à disposição as medidas indicadas na figura, calcule a distância do ponto [tex]C[/tex] ao ponto [tex]D[/tex].
Medição indireta

3) Dados dois segmentos de comprimentos [tex]m[/tex] e [tex]n[/tex], construa um segmento que tenha como comprimento a média geométrica dos dois, usando apenas régua não graduada e compasso.

4) Use semelhança de triângulos para provar que se [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex] são cordas distintas de uma mesma circunferência que se intersectam em um ponto [tex]P[/tex], então [tex]AP \cdot PB = CP \cdot PD[/tex].
Sugestão: Leia sobre ângulo inscrito numa circunferência em http://clubes.obmep.org.br/blog/angulo-central-e-angulo-inscrito/.

IV – Figuras semelhantes

Podemos falar de semelhança no estudo de outras figuras e não apenas no estudo de triângulos. E esse tipo de semelhança aparece, também, em situações cotidianas das pessoas. Por exemplo, vocês já devem ter ouvido alguma reclamação do tipo:

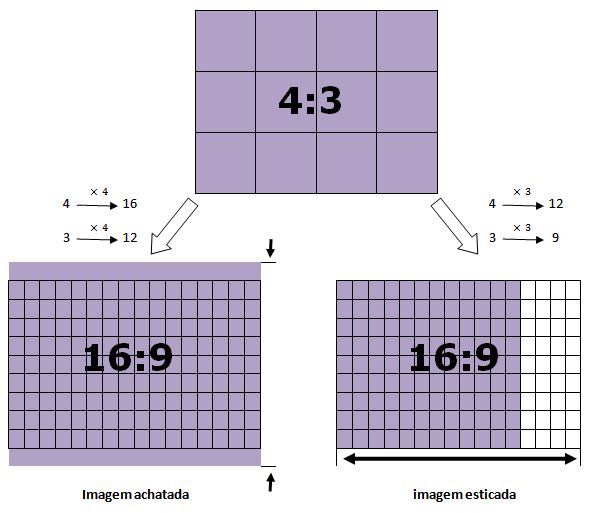
  • Por que a imagem da minha TV fica esticada (ou achatada)?
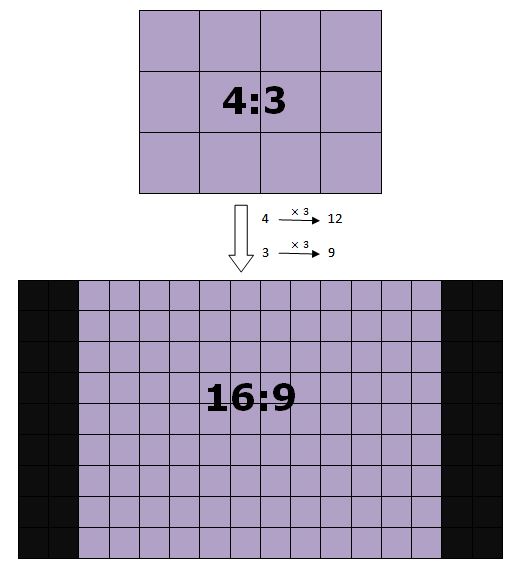
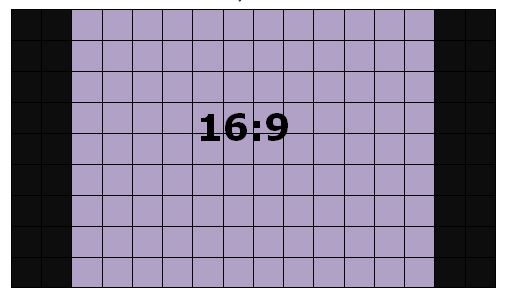
  • Por que aparecem barras laterais em torno da imagem, quando eu assisto determinados filmes no computador?

Pois é, a resposta para essas perguntas pode estar na semelhança de retângulos: um caso particular da semelhança definida a seguir.

Definição:
Duas figuras [tex]F_1[/tex] e [tex]F_2[/tex] são ditas semelhantes se existir uma correspondência biunívoca entre os seus pontos, de modo que para quaisquer dois pontos distintos [tex]P[/tex] e [tex]Q[/tex] de [tex]F_1[/tex] os pontos correspondentes [tex]P'[/tex] e [tex]Q'[/tex] em [tex]F_2[/tex] são tais que [tex]\dfrac{PQ}{P’Q’}[/tex] é constante.

Se vocês não conseguiram enxergar como a semelhança pode fornecer uma possível explicação para as imagens esticadas/achatadas e para o aparecimento de barras laterais que citamos no início deste tópico, ou acreditam que isso ocorre apenas porque as televisões modernas são maiores, cliquem no próximo botão antes de irem para os problemas propostos na Atividade 3.

Em um passado não muito longe, as TVs utilizavam a proporção 4:3 nas suas telas – para cada quatro partes iguais na largura, três partes na altura. Mas, atualmente, com a transmissão digital, a indústria passou a trabalhar com telas que usam principalmente a proporção 16:9 (widescreen), embora existam telas 21:9 (a super widescreen).
tv4
Quando assistimos algo produzido no passado em uma TV mais moderna, a TV tenta adaptar um conteúdo 4:3 para uma proporção 16:9. Assim “sobra imagem” na altura da tela ou “falta imagem” para a largura da tela, conforme se pode ver na figura abaixo, e isso pode provocar um “achatamento” ou um “esticamento” da imagem para quem assiste.
tv51
As barras pretas na lateral aparecem quando se configura uma televisão mais moderna para não deformar o conteúdo 4:3 . Neste caso, a televisão centralizará a imagem e exibirá as barras laterais para ocupar o espaço não preenchido.
tv6
É bom salientar que esses processos ocorrem não pelo tamanho, supostamente, maior das televisões modernas: ocorre pela não proporção entre as medidas das telas das tvs mais antigas e as das tvs mais modernas: [tex]\dfrac{4}{3}\ne \dfrac{16}{9}[/tex]. É um problema de proporção e não simplesmente de tamanho…

tv7tv7tv7tv7tv7

Resolvam e justifiquem as soluções dos problemas a seguir.

1) Verifiquem experimentalmente se é possível construir polígonos de mesmo tipo com lados proporcionais, mas que não sejam semelhantes.

2) Mostrem que dois quadrados quaisquer são semelhantes.

3) Mostrem que dois círculos quaisquer são semelhantes.

V – Escalas

Quando vamos representar algo por meio de um desenho ou de uma maquete, queremos que a representação seja semelhante, havendo, portanto, uma proporcionalidade entre medidas de comprimento da representação e as medidas reais correspondentes do representado. Essa constante de proporcionalidade é chamada de escala e matematicamente é assim definida:

[tex]E = \dfrac{d}{D}[/tex], com:
[tex]E[/tex] – escala; [tex]d[/tex] – medida no desenho; [tex]D[/tex] – medida real.

  • Assim uma escala 1:10.000 indica, por exemplo, que cada medida 1cm no desenho representa 10.000 cm na medida real.

planta escala

  • Na figura abaixo, a escala gráfica do primeiro mapa mostra que cada 1 centímetro (cm) medido no mapa corresponde a 25.000.000 cm, ou seja, 250.000 m, ou ainda, 250 km na medida real. Na mesma figura, no segundo mapa, estado do Rio de Janeiro, vemos graficamente que cada 1 centímetro (cm) medido no mapa, corresponde a 40 quilômetros (km) na realidade. O segundo mapa foi o que chamamos de ampliado, ou seja, foi utilizada uma escala maior: o denominador foi diminuído, logo a razão (escala) é maior.

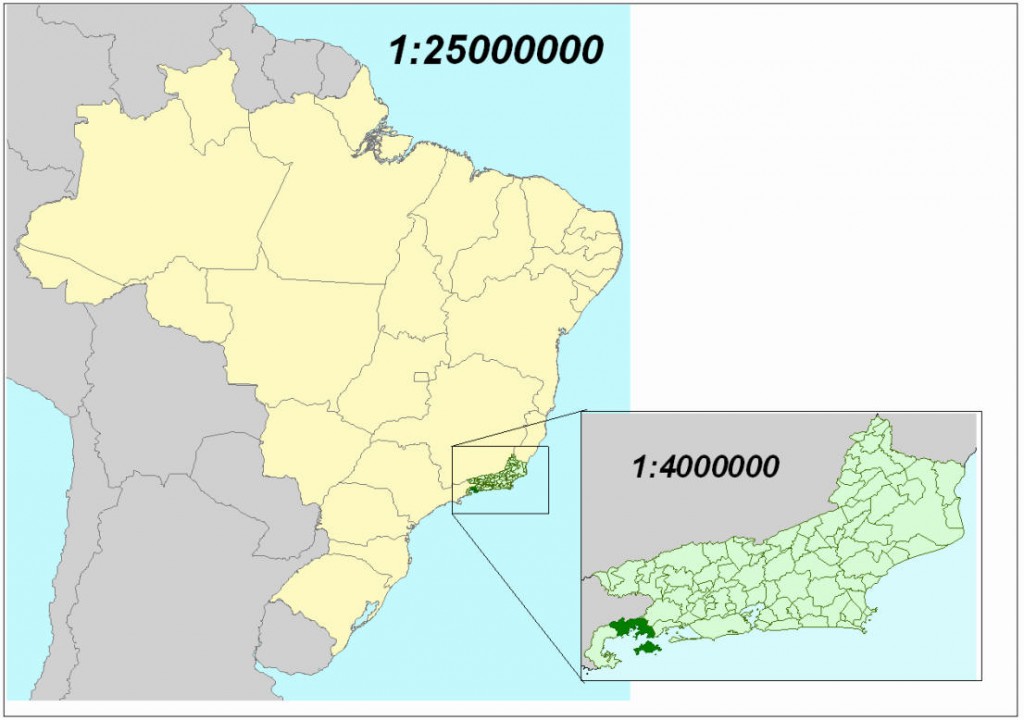
escala2

Esse é um assunto bem bacana, não é? Então, que tal ampliar o conhecimento de vocês sobre escala, resolvendo alguns problemas? É só clicar no botão Atividade 4.

Resolvam e justifiquem as soluções dos problemas a seguir.
1) (ENEM 2012) Um biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir.
escalas enem

Qual é a árvore que apresenta a maior altura real?

2) O Professor Robério imprimiu uma foto da Arena Amazônia que estava na escala 1: 6 000 000 em uma folha de papel A4, no modo paisagem.
Após a impressão, percebeu que a gravura ocupava apenas [tex]\dfrac{1}{9}[/tex] da página conforme figura.
Arena Amazônia

A partir do observado, ele percebeu que poderia aumentar o tamanho de sua área de impressão nove vezes.
Qual a escala que ele deve usar para fazer a impressão na página inteira?

3) A Rural Willys é um utilitário que foi produzido no Brasil nas décadas de 50, 60 e 70. Abaixo mostramos um desenho de uma Rural e uma tabela contendo suas principais dimensões.
escala3
escala 4

Fonte: http://ruralwillys.tripod.com/especifica/especifica.htm

Uma miniatura perfeita do veículo foi produzida tendo a distância entre os eixos de 5cm.
Qual a escala utilizada na confecção da miniatura?
Determinem as outras medidas da miniatura.
escala5

4) Pesquisem o que é um escalímetro; como utilizá-lo; modelos existentes; etc.

VI – Homotetia

No desenvolvimento de determinadas tarefas, pode ser necessário fazer ampliações ou reduções de figuras geométricas. As escalas podem ajudar, mas, na prática, como fazer uma ampliação/redução?
Podemos usar homotetia e obter ampliação ou redução de uma figura, a partir de um ponto fixo. Mas o que é homotetia?
É o que vamos ver neste tópico; mas, antes, é bom que você já saiba que máquinas copiadoras que fazem ampliações ou reduções geralmente utilizam homotetia como princípio básico dos seus processos de funcionamento.

Definição:
Sejam [tex]O[/tex] um ponto e [tex]k[/tex] um número real não nulo.
Homotetia de centro [tex]O[/tex] e razão [tex]k[/tex] de uma figura [tex]F[/tex] é uma transformação geométrica que associa a cada ponto [tex]M[/tex] de [tex]F[/tex] o ponto [tex]M'[/tex] assim definido:

  • se [tex]k[/tex] for positivo, [tex]k > 0[/tex], [tex]M'[/tex] é o ponto da semirreta [tex] OM[/tex], de origem [tex]O[/tex], tal que [tex]OM’= k\cdot OM[/tex];
  • se [tex]k[/tex] for negativo, [tex]k \lt 0[/tex], [tex]M'[/tex] é o ponto da semirreta oposta à semirreta [tex]OM[/tex], de origem [tex]O[/tex], tal que [tex]OM’=(-k)\cdot OM[/tex].

Vejam dois exemplos de figuras obtidas por homotetia.

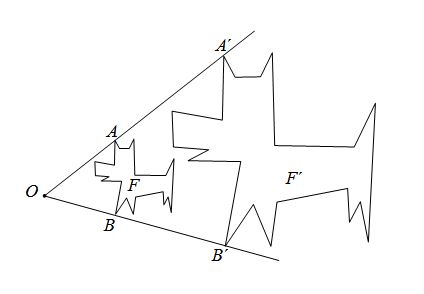
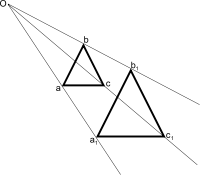
homotetia1      Homotetia

Não se assustem, a definição é meio complicada mesmo. Mas, neste momento, vocês só terão que saber como utilizar a homotetia para ampliar ou reduzir figuras e terem a certeza de que as figuras obtidas são semelhantes à figura inicial.
Para um melhor entendimento de como obter uma figura por homotetia, a partir de uma figura inicial:

  • utilizem este applet;
  • leiam este texto, extraído de Construções Geométricas – Vol.1. Consórcio CEDERJ/UENF/UERJ/UFF/UFRJ/UFRRJ/UNIRIO/Fundação CECIERJ;
  • assistam a este vídeo.

Agora chegou a vez de vocês obterem figuras por homotetia. Cliquem no botão da Atividade 5 e boa diversão!

Vamos realizar um experimento?

  • Desenhem numa cartolina uma figura que será nosso padrão.
  • Realizem, por homotetia, quatro ampliações e quatro reduções da figura padrão, anotando as razões de semelhança utilizadas. Nessas oito ações, utilizem, necessariamente, as seguintes razões de semelhança:[tex] 3, \, -2, \, \dfrac{1}{3}, -\dfrac{1}{4}[/tex]. As demais razões de semelhança ficam a critério do grupo.
  • Recortem todas as figuras e pesem-nas utilizando uma balança de precisão.
  • Qual a relação entre os “pesos” dessas figuras e seus tamanhos?

VII – Atividades de campo

Agora que vocês já conhecem algumas das proporções da Geometria, que tal utilizarem o que aprenderam para se divertir?
Escolham um tema, cliquem sobre ele e boa diversão!

O Google Maps é um serviço gratuito para visualização de mapas e imagens de satélite da Terra. Graças ao Google Maps, é possível traçar rotas nos mapas, visualizar grandes centros urbanos com zoom e cadastrar empresas e negócios no mapa.
Caso consigam visualizar sua cidade utilizando o Google Maps:

  • Tracem a rota da casa de um de vocês até a escola e vejam a distância real fornecida para esse trajeto.
  • Imprimam o mapa e utilize uma linha sobre o trajeto destacado, em seguida estiquem a linha e meçam a distância do percurso no desenho.
  • Deixem as duas medidas na mesma unidade de comprimento e descubram a escala do mapa. Comparem o valor encontrado com o fornecido no canto inferior direito da tela do Google Maps.

– Registrem a atividade com fotos ou vídeo.
– Em um relatório, descrevam como foi realizada a atividade e registrem os cálculos, comentários e conclusões.

  • O que é um pantógrafo?
  • Utilizem este aplicativo do GeoGebra para entender o funcionamento de um pantógrafo.
  • Realizem uma oficina para a construção de um pantógrafo.
  • Utilizem o pantógrafo construído na oficina para ampliar os escudos dos seus Clubes.

– Registrem a atividade com fotos ou vídeo.
– Em um relatório, descrevam como foi realizada a oficina, anexem a ampliação do escudo e registrem os cálculos, comentários e conclusões.

Realizem um experimento que permita calcular a altura de um objeto, cuja medição direta é inacessível, a partir da medição de sombras e do uso de semelhança de triângulos.

– Registrem a atividade com fotos ou vídeo.
– Em um relatório, descrevam como foi realizado o experimento e registrem os cálculos, comentários e conclusões.

1) Realizem medições de dependências de sua escola e desenhem a planta baixa delas, tendo o cuidado de utilizarem a escala conveniente e as representações gráficas existente no desenho de plantas.
2) Pesquisem sobre as diferenças e semelhanças (não matemáticas) entre engenheiros e arquitetos.

– Registrem a atividade com fotos ou vídeo.
– Em um relatório, descrevam como foi realizada a atividade e registrem os cálculos, as plantas desenhadas, comentários e conclusões. Incluam, também nesse relatório, o resultado da pesquisa sobre arquitetos e engenheiros.

VIII – Material que pode ajudar…

Disponibilizamos aqui textos, sites e vídeos que podem ajudá-los no desenvolvimento das atividades propostas nesta Sala.
Esperamos que o material lhes seja útil.

Galeria de vídeos

Aqui vocês encontram vídeos que poderão utilizar nas suas pesquisas.
Cliquem na figura correspondente ao vídeo que vocês querem assistir: na janela que irá abrir, é só clicar na setinha e, depois de assistir ao vídeo escolhido, é só fechar a janela que se abriu.

v6
Discovery na Escola – Conceitos de Álgebra
Razão e Proporção 		Khan Academy em Português
Conceitos básicos de triângulos semelhantes

v1 v2
Novo Telecurso – Matemática – Ensino Fundamental
Aula 46 – Razão e proporção 		Novo Telecurso – Matemática – Ensino Fundamental
Aula 47 – Teorema de Tales

v3 v4
Novo Telecurso – Matemática – Ensino Fundamental
Aula 48 – Semelhança de Figuras / Escalas 		Novo Telecurso – Matemática – Ensino Fundamental
Aula 49 – Proporção inversa

v10 v11
Isto é Matemática
O Raio da Terra 		Khan Academy em Português
Exemplos de problemas com triângulos semelhantes

Textos e sites

Disponibilizamos abaixo links de textos que vocês poderão utilizar nas diversas atividades propostas nas salas sobre Proporção em Geometria.

❐ A Geometria e as distâncias astronômicas distâncias astronômicas na Grécia Antiga – Geraldo Ávila    (Último acesso em 30/06/20)
❐ Arquiteto x Engenheiro Civil: conheça as diferenças e semelhanças dessas duas profissões    (Último acesso em 30/06/20)
❐ As diferenças e semelhanças entre engenheiros e arquitetos    (Último acesso em 30/06/20)
❐ Instrumentos Científicos    (Último acesso em 30/06/20)
❐ O Princípio da similitude de Galileu Galilei    (Último acesso em 30/06/20)

 

Bons estudos, pessoal!

Mas, e as aranhas gigantes??????

 carinha19

Como disse anteriormente, a geometria e a proporção vão acabar com esse problema.

 
Os Clubes no combate às aranhas gigantes…

Se vocês também ficaram curiosos com a notícia da Apresentação do Tema, ouçam uma explicação matemática a respeito de ataques por criaturas descomunais, dada pelo professor Humberto José Bortolossi, do Instituto de Matemática da Universidade Federal Fluminense, assessorado por sua Equipe e pelo cientista Galileu Galilei.

A altura e o peso de uma aranha dependem, entre outros fatores, da espécie, do gênero e de sua alimentação. Mas, certamente, não existem aranhas gigantes como aquelas que aparecem nos filmes de terror.
Imagine, por exemplo, a situação de duas aranhas semelhantes, uma com um centímetro de altura e outra 100 vezes mais alta, isto é, com um metro.
A largura de cada pata da aranha gigante seria 100 vezes maior do que a da outra, então, o calibre desta pata forneceria uma área de apoio 10.000 vezes maior.
Só que o peso dessa aranha gigante não seria 10.000 vezes maior, mas sim 1.000.000 de vezes maior! Isso porque o peso do animal cresce de acordo com o volume e não com a área.
Com todo esse peso, a aranha gigante não conseguiria se sustentar de pé sobre suas oito patas.
Por trás disso está o Princípio da Similitude, enunciado pela primeira vez por Galileu Galilei, em 1638.
Se os filmes de terror fossem dirigidos por físicos ou matemáticos, talvez as aranhas de um metro, tivessem não 8, mas sim, 800 patas cada uma!

Abaixo apresentamos uma breve discussão do Princípio da Similitude de Galileu Galilei. Quem entendeu a discussão de semelhança e proporção, não terá problema para compreendê-lo!

A Teoria da Similitude (Semelhança)

Em sua obra Discorsi e Dimostrazioni Mathematische, datada de 1638, Galileu Galilei apresenta um princípio conhecido por Princípio da Similitude:

“Nenhum organismo biológico ou instituição humana, que sofra uma mudança de tamanho e uma consequente mudança na escala de proporções, não passa por isso sem modificar sua forma ou conformação.”

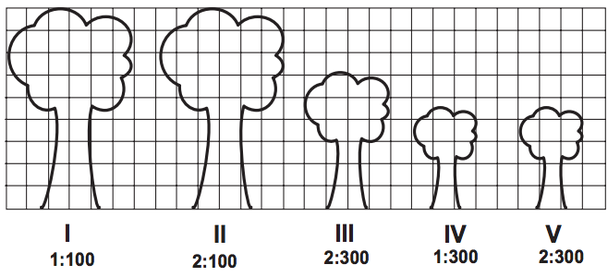
Assim, segundo esse princípio, se um organismo biológico aumentar o seu tamanho, ele vai ter que mudar a sua estrutura. Vamos tentar entender o porquê.

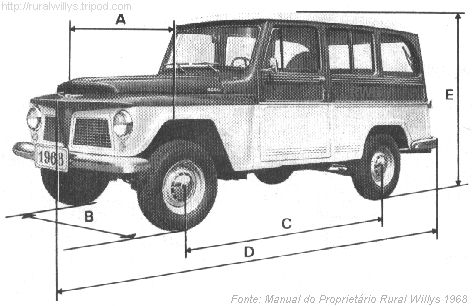
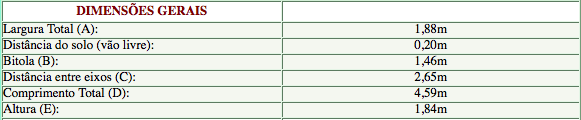
Considere, por exemplo, a situação de dois animais semelhantes tais que um deles tem o dobro da escala do outro. A “espessura” de um osso do animal maior será 4 vezes maior do que a “espessura” do osso correspondente do animal menor, mas este osso terá que suportar 8 vezes mais peso! Portanto, a estrutura óssea do animal maior será bem mais frágil, se comparada com a do animal menor. Pelo Princípio da Similitude, uma “versão maior” do animal menor preferirá mudar a sua estrutura (por exemplo, aumentando mais do que 4 vezes a “espessura” dos ossos) para garantir robustez.
Para entender um pouco melhor essa argumentação, acompanhe o exemplo apresentado a seguir.

  • Quando dobramos o tamanho do segmento, obtemos o equivalente a dois segmentos.
  • Quando dobramos o tamanho dos quadrados, ficamos com o equivalente a 4 quadrados (observe que [tex]2^2=4[/tex]).
  • Quando dobramos o tamanho do cubo, ficamos com o equivalente a 8 cubos, isto é, [tex]2^3[/tex] cubos!

Como o peso de um animal depende do volume dele, quando dobramos o tamanho de um bicho, seu peso fica multiplicado por [tex]2^3[/tex].
Então, vamos refazer a conta para as aranhas gigantes:
(i) se o tamanho da aranha aumentar em 100 vezes, a área da seção reta de suas patas, isto é, a área de apoio dada por elas, se multiplicaria por [tex]100^2[/tex]. Ficaria 10.000 maior!
(ii) Já o peso da aranha, assim como seu volume, se multiplicaria por [tex]100^3[/tex], ficaria 1.000.000 (um milhão) de vezes maior!

E faltariam patas para sustentar tanto peso!

Tá, entendi: aranhas gigantes de verdade não existem.
Fiquei apavorado à toa…

 carinha10

Em tempo: o vídeo que assustou você e muitos internautas é uma peça publicitária, no mínimo original, feita para o lançamento do último livro de uma trilogia, em Portugal.

 

E      e  u       a   c   r   e   d   i   t   e   i . . .

 

 carinha7

 

Sugestões de material para os professores:
➨ Geometria    (Extraído do Portal do MEC)
➨ Semelhança    (Último acesso em 30/06/20)
➨ Sombra, semelhança e proporção    (Último acesso em 30/06/20)

Equipe COM – OBMEP

Agosto de 2015.

Figuras, vídeos e material eventual extraídos de:
➨ Infowester responde    (Último acesso em 12/12/22)
➨Licenças sob Domínio público via Wikimedia Commons
➨ Wikipedia    (Último acesso em 12/12/22)
➨ YouTube    (Último acesso em 12/12/22)

Link permanente para este artigo: http://clubes.obmep.org.br/blog/atividade-proporcao-em-geometria-2/

Deixe uma resposta