|
Apresentaremos aqui algumas definições e propriedades básicas de geometria para ajudar no entendimento das pavimentações de Escher.
|
Isometrias e simetrias
Para entendermos melhor os padrões das pavimentações de Escher, é importante conhecermos alguns movimentos que podemos fazer com figuras do plano de modo que elas mudem de posição, mas mantenham as suas aparências: formas e tamanhos. Esses movimentos são estudados na matemática com o nome de Isometrias.
Sem muito rigor, as isometrias são transformações geométricas que preservam as distâncias entre pontos e as amplitudes de ângulos e, assim, transformam uma figura em outra “geometricamente igual”: cada segmento da figura transformada tem o mesmo tamanho do seu correspondente na figura original, podendo variar a direção ou o sentido, e cada ângulo transformado mantém a sua amplitude inicial. Portanto, uma isometria pode mudar somente a posição da figura na qual ela foi aplicada.
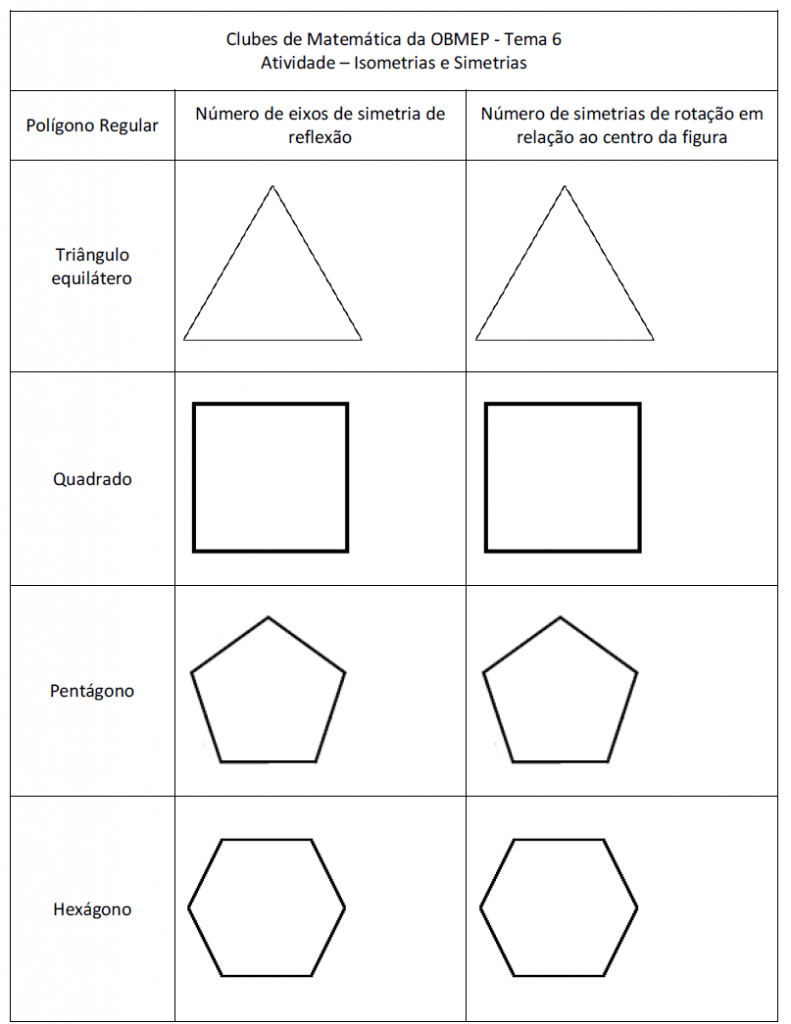
Existem exatamente quatro tipos de isometrias no plano:
- translação,
- rotação,
- reflexão,
- reflexão com deslizamento.
A ideia aqui não é definirmos formalmente cada uma dessas transformações, até porque isso fugiria aos propósitos e aos objetivos desta Sala de Atividades, mas sim disponibilizar material para que vocês aprendam a reconhecer quando esses quatro movimentos foram aplicados em figuras planas. Como a reflexão com deslizamento é o resultado de uma reflexão seguida de uma translação, ou de uma translação seguida de uma reflexão, basta que vocês reconheçam os três primeiros tipos de isometrias.
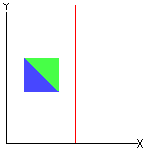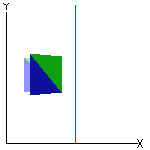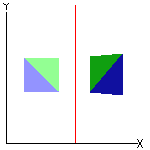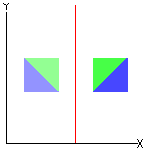
Que tal começar com as figuras abaixo?
 |
 |
 |
|
|
|
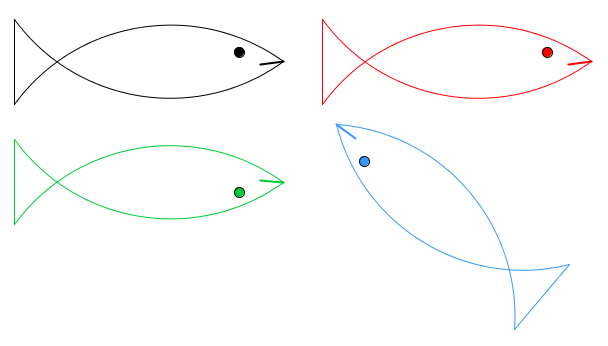
Vejam, a seguir, algumas características das três transformações.
|
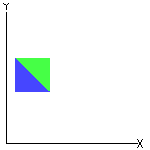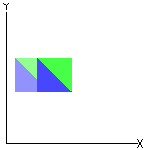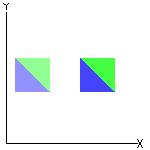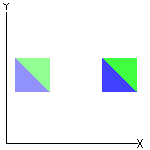
☞ Em uma translação:
✓ Qualquer segmento de reta é transformado em um segmento de reta paralelo e com o mesmo comprimento. |
|
|
☞ Em uma rotação:
✓ Qualquer segmento de reta é transformado em um segmento de reta com o mesmo comprimento (não necessariamente paralelo). Observação: Para se definir uma rotação é necessário fixar um ponto do plano, digamos [tex]O[/tex] e um ângulo segundo o qual será feita a rotação, digamos um ângulo de medida [tex]\alpha[/tex]. Nesse caso, todos os pontos da figura inicial rodam em torno do ponto [tex]O[/tex], segundo um ângulo de medida [tex]\alpha[/tex] e um sentido. O sentido da rotação pode ser o mesmo dos ponteiros de um relógio (dito sentido negativo) ou contrário ao sentido dos ponteiros do relógio (dito sentido positivo). |
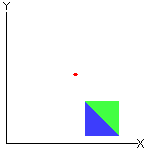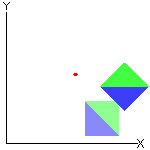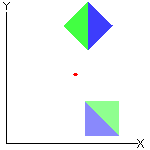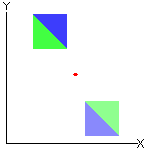
|
|
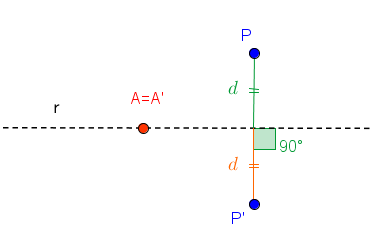
☞ Em uma reflexão:
✓ Qualquer segmento de reta é transformado em um segmento de reta com o mesmo comprimento (não necessariamente paralelo). Observação: Para se fazer uma reflexão, precisamos de uma reta, digamos [tex]r[/tex]. Nesse caso, a reflexão em torno de [tex]r[/tex] deixa invariantes os pontos de [tex]r[/tex] (transforma pontos de [tex]r[/tex] neles próprios) e cada ponto [tex]P[/tex] que não pertence a [tex]r[/tex] é transformado em um ponto [tex]P'[/tex] tal que [tex]r[/tex] é a mediatriz do segmento [tex]PP'[/tex] (a distância de [tex]P[/tex] a [tex]r[/tex] é igual à distância de [tex]P'[/tex] a [tex]r[/tex] e o segmento de reta determinado por [tex]P[/tex] e [tex]P'[/tex] é perpendicular à reta [tex]r[/tex]). |
Gifs animados extraídos de: Science U |
Existe um tipo de reflexão – reflexão por um ponto – que equivale a uma rotação de [tex]180^{\circ}[/tex], portanto não faremos nenhuma observação sobre esse tipo de reflexão.
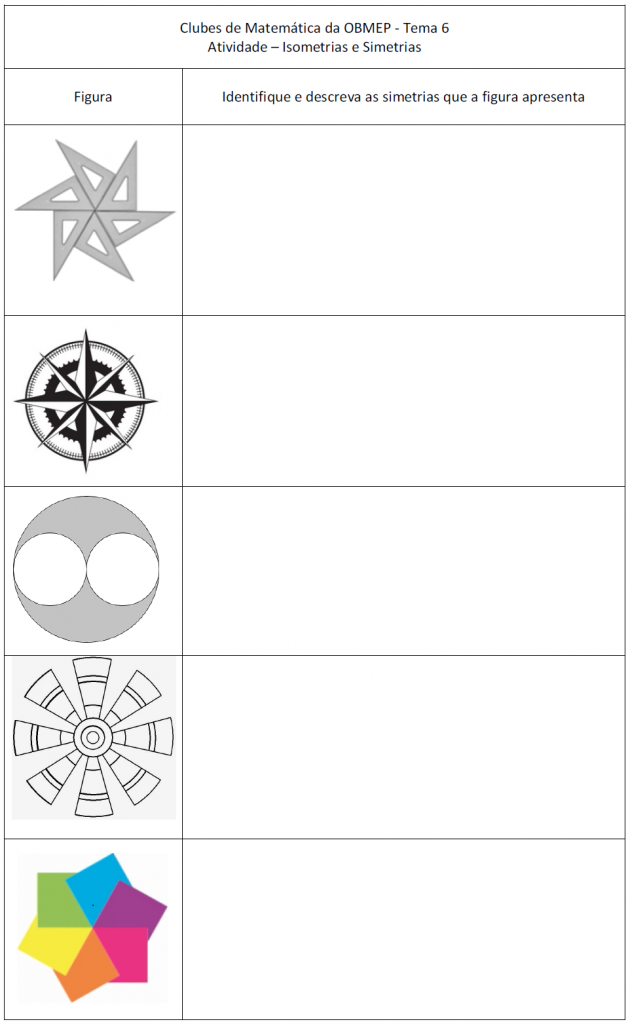
Como as isometrias são transformações que não distorcem as formas e mantêm os tamanhos das figuras, cada isometria é uma transformação geométrica que permite movimentar uma figura sem que suas propriedades métricas sejam alteradas. Portanto, tem sentido procurarmos figuras cujas imagens produzidas por isometrias coincidam com as respectivas figuras originais. Essas figuras têm um nome especial na matemática, vocês as conhecem?
Novamente, sem muito rigor, dizemos que uma figura é simétrica (ou tem simetria) quando for possível encontrar uma isometria (diferente da identidade) que transforme essa figura nela própria. Nesse caso, a isometria que deixa uma figura F invariante é dita uma simetria da figura F. Assim uma figura pode ter simetria de translação, simetria de reflexão, simetria de rotação ou simetria de reflexão deslizante ou nenhuma simetria.
Vale observar que, embora rigorosamente falando simetria seja uma propriedade de algumas figuras, é comum que, de maneira informal, duas figuras sejam consideradas simétricas quando uma pode ser obtida a partir da outra por meio de isometrias.
Assistam aos próximos vídeos e observem as diferenças entre cada uma dessas isometrias. Particularmente o primeiro vídeo trata da reflexão por um ponto.
Cliquem na figura correspondente ao vídeo que vocês querem assistir: na janela que irá abrir, é só clicar na setinha.
 |
 |
 |
Depois de assistir ao vídeo, é só fechar a janela que se abriu.
Vocês também podem aprender sobre simetrias assistindo ao vídeo a seguir, que apresenta o trabalho desenvolvido pelo professor de Matemática Edson Thó Rodrigues, de João Pessoa (PB) e vencedor do Prêmio Victor Civita 2011. Por meio de experiências com espelhos, o professor propôs que a turma entendesse, na prática, o conceito de simetria e as relações entre ângulos e lados de polígonos.
Para assistir ao vídeo, é só clicar na setinha.
Antes de encerrarmos estas breves considerações, deixaremos aqui duas atividades, uma pergunta intrigante e uma sugestão de leitura.
Bons estudos!
Equipe COM – OBMEP
➨ ARTE NO PAINT (Último acesso em 14/08/18)
➨ Catavento (Último acesso em 14/10/15)
➨ GEOGRAFIA Newton Almeida (Último acesso em 14/08/18)
➨ ScienceU (Último acesso em 14/08/18)
➨ Licenças sob Domínio público via Wikimedia Commons