✏ Link da Sala para dispositivos da Apple.
Uma visão geral
O estudo das funções é de grande importância na Matemática e em várias outras áreas, pois as funções são usadas para descrever e modelar muitos fenômenos e processos em diversas áreas, incluindo Física, Engenharia, Economia, Biologia, Química, Ciência da Computação e outras. As funções são essenciais para a compreensão da Matemática em geral, pois elas fornecem uma estrutura para analisar relações entre variáveis, tendo inúmeras aplicações práticas em muitas áreas do conhecimento, como as que seguem.
● Modelagem: As funções são frequentemente usadas para modelar fenômenos do mundo real, como o movimento de objetos, a evolução de populações, o crescimento de culturas bacterianas e muitos outros. O estudo das funções permite que os pesquisadores desenvolvam modelos matemáticos precisos que podem ser usados para prever e entender melhor esses fenômenos.
● Análise de dados: O estudo das funções é essencial para a análise de dados em muitas áreas, como Estatística e Ciência de Dados. As funções são usadas para descrever relações entre variáveis e para identificar padrões em conjuntos de dados.
● Cálculo: As funções são fundamentais para o Cálculo, que é uma das áreas mais importantes da Matemática. O Cálculo é usado para estudar as propriedades das funções e para resolver problemas relacionados a limites, derivadas e integrais.
● Engenharia: As funções são usadas em muitas áreas da Engenharia, incluindo Engenharia Mecânica, Engenharia Elétrica e Engenharia Civil. As funções são usadas para modelar sistemas físicos e para analisar dados de experimentos e simulações.
● Programação de computadores: As funções são usadas na programação de computadores para criar algoritmos e para desenvolver programas que realizam tarefas específicas. As funções são fundamentais para a estruturação do código e para a criação de programas.
Estabelecendo uma linguagem inicial
Considere a situação a seguir.
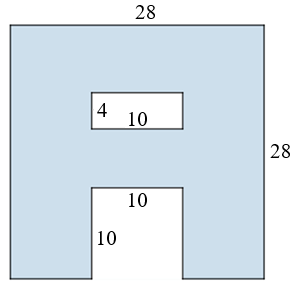
E se os lados do quadrado medissem [tex]6\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]6\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]7\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]7\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]9\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]9\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]11\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]11\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]12,2\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]12,2\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]14,6\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]14,6\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]23,786\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]23,786\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]25\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]25\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]26\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]26\text{ cm}[/tex]. Qual seria a área?
E se os lados do quadrado medissem [tex]2\text{ cm}[/tex] e os lados do retângulo medissem [tex]4\text{ cm}[/tex] e [tex]2\text{ cm}[/tex]. Qual seria a área?
E se …

Bem, já deu para perceber que poderíamos ficar até amanhã à tarde propondo novas medidas para o quadrado e o retângulo que poderão ser retirados do quadrado inicial, não é?
Essa é apenas uma situação muito simples para ilustrar que, se não conseguirmos estabelecer uma relação entre os dados de determinados problemas, podemos gastar inutilmente o nosso tempo fazendo contas desnecessárias…
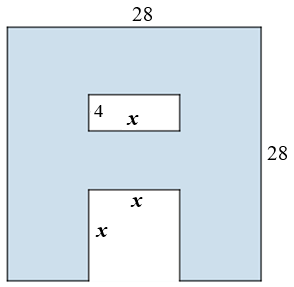
No caso dessa situação que colocamos, podemos observar que a medida da área definida pela letra A depende de maneira única da medida do comprimento do lado do quadrado menor (e consequentemente do lado de comprimento diferente de [tex]4\text{ cm}[/tex] do retângulo). Perceba que, se representarmos a medida do comprimento do lado do quadrado menor por [tex]x[/tex] podemos modelar de maneira geral o problema e calcular a área definida pela letra A a partir desse [tex]x[/tex]: [tex]\boxed{28^2-x^2-4x}.[/tex]
Simbolicamente: [tex]x \mapsto 28^2-x^2-4x.[/tex]
Mesmo em situações muitíssimo complexas de modelagem do mundo real essa ideia está presente em várias delas: ao analisarmos uma possível relação entre elementos de dois conjuntos não vazios, [tex]C_1[/tex] e [tex]C_2[/tex], é possível estabelecer uma relação de dependência entre esses elementos, de modo que para cada elemento de [tex]C_1[/tex] corresponde um único elemento de [tex]C_2.[/tex]
Como um símbolo [tex]x[/tex] que serve para designar, por exemplo, elementos de um conjunto é chamado de variável, vão nos interessar na nossa conversa as relações nas quais duas variáveis [tex]x[/tex] e [tex]y[/tex] são tais que a cada elemento [tex]x[/tex] de [tex]C_1[/tex] corresponde um e somente um elemento [tex]y[/tex] de [tex]C_2[/tex].
\begin{eqnarray*}
C_1 &\rightarrow & C_2\\
x&\mapsto & y
\end{eqnarray*}
Mas, matematicamente,
que objeto é esse que vamos estudar?
Vamos formalizar matematicamente essa ideia, lembrando que definir um objeto é simplesmente lhe dar um nome, e definir o objeto central desta Sala: Função.
Usaremos a notação
[tex]\qquad \begin{eqnarray*}
f:A &\rightarrow & B\\
x&\mapsto & y
\end{eqnarray*} [/tex]
para indicar que [tex]f[/tex] é a função de [tex]A[/tex] em [tex]B[/tex] que faz corresponder a [tex]x[/tex] o valor [tex]y[/tex]. É usual representar o único elemento [tex]y[/tex] associado a [tex]x[/tex] por [tex]f(x)[/tex].
Na Matemática é comum darmos nomes especiais a objetos de um mesmo tipo aos quais fazemos referências várias vezes. Além de nomes, quando conveniente, são criadas representações simbólicas (notação) para resumir ainda mais a ideia por trás do nome e facilitar o trabalho que virá pela frente.
Observe que, ao definirmos função, utilizamos três outros “objetos” – dois conjuntos e uma regra – que serão mencionados com frequência. Assim, para não termos que ficar falando ou escrevendo a todo tempo que o elemento [tex]x[/tex] está no “primeiro” dos conjuntos nos quais será aplicada a regra, chamamos esse primeiro conjunto ([tex]A[/tex] na definição do parágrafo anterior) de domínio da função e, no caso de uma função [tex]f[/tex], o denotamos de forma genérica por [tex]D(f)[/tex]. Assim, bastará escrever [tex]x\in D(f)[/tex] para dizer que “o elemento [tex]x[/tex] pertence ao domínio da função [tex]f[/tex]”. O segundo conjunto com os valores aos quais os elementos do domínio são associados ([tex]B[/tex] na definição acima) é chamado contradomínio da função e no caso de uma função [tex]f[/tex], às vezes, é representado por [tex]CD(f)[/tex]. O valor [tex]y=f(x)[/tex] é chamado de imagem de [tex]x[/tex] por [tex]f[/tex], mas também dizemos que [tex]y=f(x)[/tex] é o valor de [tex]f[/tex] em [tex]x[/tex].
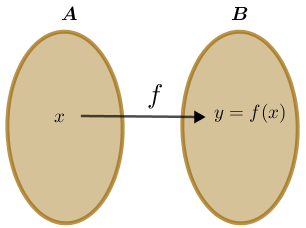
Dizemos, ainda, que [tex]x[/tex] é a variável independente (ou livre), porque ela é livre para assumir qualquer valor em [tex]D(f)[/tex], e [tex]y[/tex] é a variável dependente, porque seu valor depende da escolha de [tex]x[/tex]. Embora seja comum representar a variável de domínio pela letra [tex]x[/tex] e a da imagem por [tex]y[/tex], isso não é uma regra rígida. Deve-se entender pelo contexto qual é a variável independente e qual é a dependente.
Nesta Sala estamos interessados no estudo de funções cujas variáveis independente e dependente são números reais. Então trabalharemos com funções que estabelecerão um tipo especial de relação entre variáveis que, na prática, representam grandezas como tempo, velocidade, posição, custo, número de unidades, etc…
Assim, para as funções que serão tratadas adiante, consideraremos [tex]D(f)\subset\mathbb{R}[/tex], [tex] CD(f)\subset\mathbb{R}[/tex] e vamos estabelecer algumas convenções:
► Quando o domínio não for especificado, consideraremos como domínio o conjunto de todos os valores cuja regra (que pode ser uma fórmula) faz sentido, ou seja, cujo resultado de sua aplicação é um número real.
► Caso não seja mencionado, consideraremos [tex]CD(f)=\mathbb{R}[/tex].
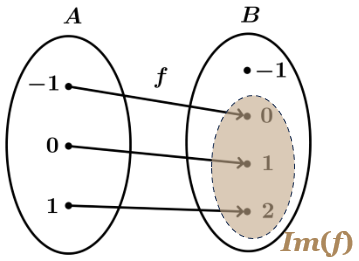
Uma função pode ser representada por um diagrama de flechas, conforme a figura a seguir.
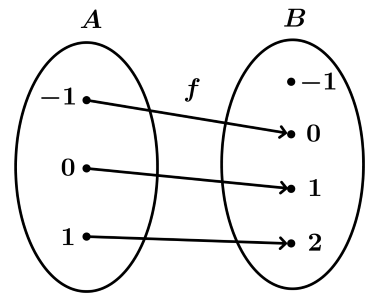
Na figura acima temos a representação de uma função [tex]f:A\rightarrow B[/tex] cuja regra que permite associar a cada elemento [tex]x \in A[/tex] um único elemento [tex]y\in B[/tex] pode ser definida por [tex]f(x)=x+1[/tex]. Observe, que neste caso:
● o domínio de [tex]f[/tex] é [tex]A=\{-1, 0, 1\};[/tex]
● o contradomínio de [tex]f[/tex] é [tex]B=\{-1, 0, 1, 2\}.[/tex]
Perceba que nem todos os elementos de [tex]B[/tex] são imagens de elementos de [tex]A[/tex]: não existe um elemento [tex]a[/tex] em [tex]A[/tex] tal que [tex]f(a)=-1.[/tex]
Essa observação ilustra outro objeto matemático ligado ao conceito de função: o conjunto imagem de uma função, ou seja, o conjunto de todos os elementos do contradomínio que são imagens de elementos do domínio.
[tex]\qquad Im(f)=\{y\in B ~|~ y=f(x) \text{ para algum } x\in A\}.[/tex]
O conjunto imagem da função [tex]f[/tex] do exemplo anterior é [tex]Im(f)=\{0, 1, 2\}.[/tex]
Nem sempre uma função é apresentada na forma padrão que definimos. Existem situações em que podemos perceber uma relação em diferentes formas de representações entre elementos de duas grandezas que podem definir funções, mas não aparecem explícitos o domínio, o contradomínio e a lei de formação dessa função. Em situações como essas, podemos destacar os conjuntos de elementos que se relacionam de modo a obter uma função ou até a lei de formação!
Vejamos dois exemplos.
A relação acima, da forma como está apresentada, ainda não define uma função, pois não foi exibido nenhum conjunto candidato a contradomínio. No entanto, como para um número natural [tex]n[/tex] qualquer, a quantidade de números primos de [tex]1[/tex] a [tex]n[/tex] é sempre um número natural, então podemos representar essa relação pela seguinte função:
[tex]\qquad \begin{eqnarray*}
p:~\mathbb{N} &\rightarrow & \mathbb{N}\\
n&\mapsto & p(n)
\end{eqnarray*}[/tex],
sendo [tex]p(n)[/tex] a quantidade de primos de [tex]1[/tex] a [tex]n[/tex].
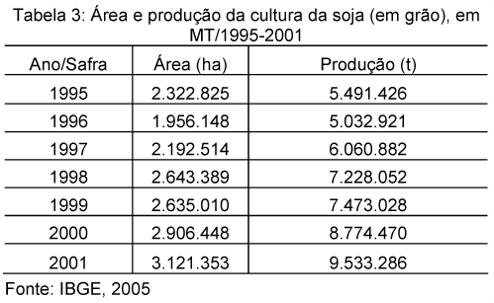
Se considerarmos [tex]A[/tex] o conjunto dos anos de 1995 a 2001, [tex]B[/tex] o conjunto dos valores que correspondem às áreas (em hectares) representados na tabela e [tex]C[/tex] o conjunto dos valores que correspondem à produção (em toneladas) também representados na tabela, teremos duas diferentes funções:
● uma função [tex]a[/tex] de [tex]A[/tex] em [tex]B[/tex], que a cada [tex]t\in A[/tex], associa um único [tex]a(t)\in B[/tex];
● uma função [tex]p[/tex] de [tex]A[/tex] em [tex]C[/tex], que a cada [tex]t\in A[/tex], associa um único [tex]p(t)\in C[/tex].
Se você precisa de mais alguns exemplos de relações que definem funções é só clicar no botão abaixo.
Outra maneira de apresentarmos uma função cujas variáveis são números reais é utilizando o que denominaremos de Gráfico da função.
O gráfico de uma função é o retrato dessa função, é uma forma de representar geometricamente o seu comportamento.
Gráfico de uma função
Para construir o gráfico de uma função cujas variáveis dependente e independente são números reais utilizamos um ambiente matemático apropriado, que é chamado de plano cartesiano.
Assim, antes de falarmos de gráficos de funções, vejamos o que é um plano cartesiano e outros conceitos.
● no par ordenado [tex](1,2~; ~3),[/tex] o primeiro elemento é [tex]1,2[/tex] e o segundo elemento é [tex]3[/tex];
● no par ordenado [tex](7~; ~2,3),[/tex] o primeiro elemento é [tex]7[/tex] e o segundo elemento é [tex]2,3[/tex];
● no par ordenado [tex](2,5~;~ 6,7),[/tex] o primeiro elemento é [tex]2,5[/tex] e o segundo elemento é [tex]6,7[/tex].
Chamamos de Plano Cartesiano, e representamos por [tex]xOy[/tex], o plano determinado por esses dois eixos. O eixo horizontal [tex]Ox[/tex] é chamado de eixo das abscissas; o eixo vertical [tex]Oy[/tex] é chamado de eixo das ordenadas e o ponto [tex]O[/tex] é chamado de origem do plano cartesiano.
Fixado um plano cartesiano, podemos representar geometricamente um par ordenado de números reais como um ponto desse plano; assim como associar a qualquer ponto desse plano um par ordenado de números reais.
Vejamos como!
➤ Dado um ponto [tex]P[/tex] no plano cartesiano [tex]xOy[/tex], a ele podemos atribuir um único par ordenado [tex](x_{_P},y_{_P})[/tex], cujo primeiro número [tex]x_{_P}[/tex] é a localização com respeito ao eixo das abscissas e o segundo número [tex]y_{_P}[/tex] é a localização com respeito ao eixo das ordenadas.
➤ Reciprocamente, para cada par ordenado [tex](a,b)[/tex] podemos associar um único ponto [tex]Q[/tex] no plano.
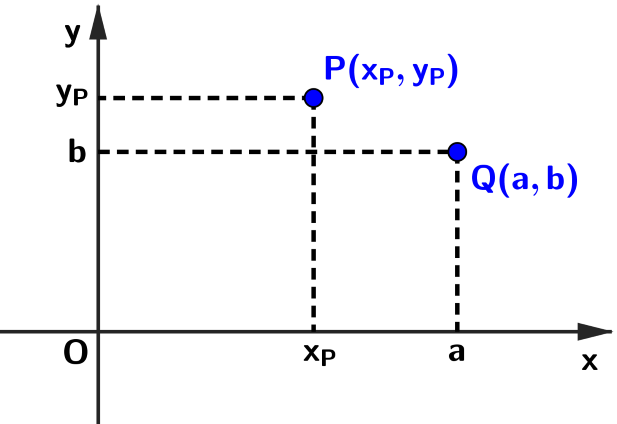
Com isso, estabelece-se uma correspondência única entre os pontos de um plano cartesiano e o conjunto dos pares ordenados de números reais.
Com a discussão feita acima, podemos observar que um par ordenado, na verdade, representa a localização de um determinado ponto no plano cartesiano e, portanto, a partir de agora, podemos olhar para um par ordenado como sendo as coordenadas de um ponto no plano cartesiano.
Assim como a reta real é o modelo geométrico para o conjunto dos números reais, o plano cartesiano é o modelo geométrico para o conjunto [tex]\mathbb{R}^2[/tex] de todos os pares ordenados de números reais.
O plano cartesiano pode ser dividido em quatro regiões, chamadas de quadrantes, conforme ilustra a figura a seguir.

Uma questão interessante sobre o plano cartesiano está relacionada à simetria de pontos. Tal noção é importante quando definimos alguns conceitos relacionados às funções como, por exemplo, função inversa, função par e função ímpar. Conhecer um pouco de simetria também pode ser útil na análise de certos problemas. Temos quatro casos de simetria de pontos no plano cartesiano:
➤ os pontos [tex](a,b)[/tex] e [tex](a,-b)[/tex] são simétricos em relação ao eixo [tex]x[/tex];
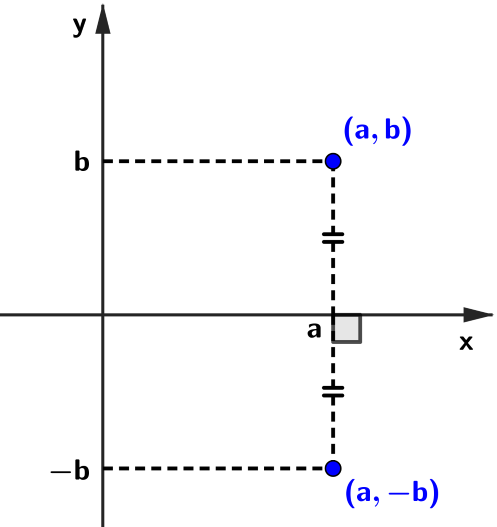
➤ os pontos [tex](a,b)[/tex] e [tex](-a,b)[/tex] são simétricos em relação ao eixo [tex]y[/tex];
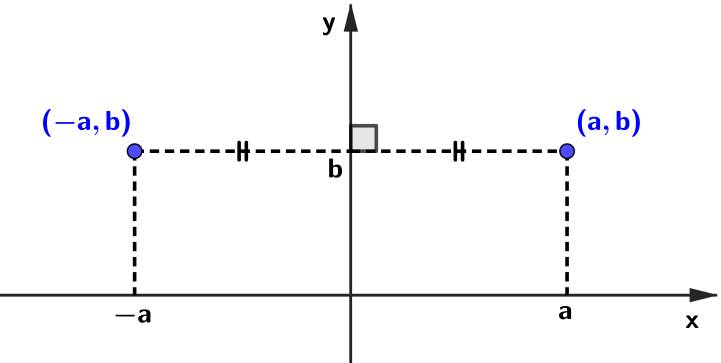
➤ os pontos [tex](a,b)[/tex] e [tex](-a,-b)[/tex] são simétricos em relação à origem;
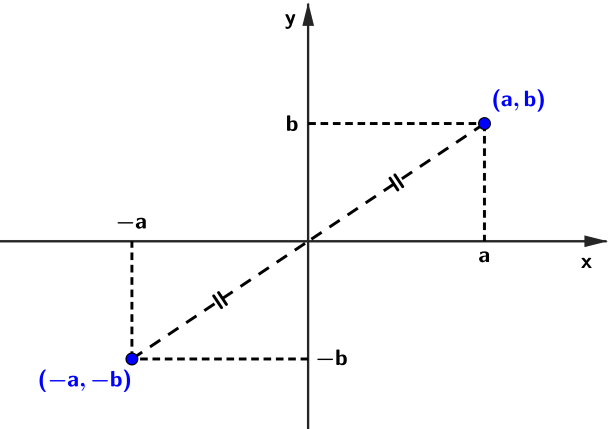
➤ os pontos [tex](a,b)[/tex] e [tex](b,a)[/tex] são simétricos em relação à bissetriz dos quadrantes 1 e 3.
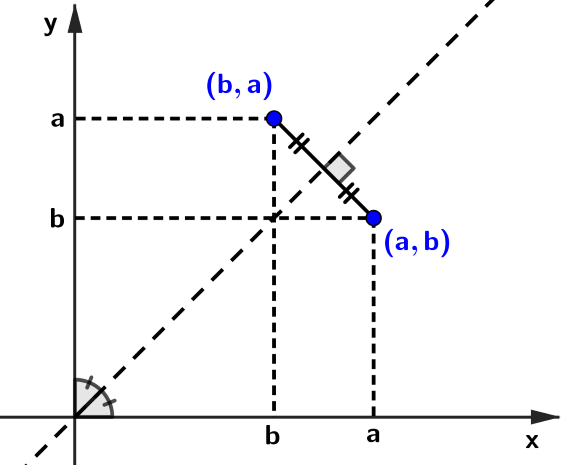
Agora, já temos condições de definir gráfico!
Definimos o gráfico da função [tex]f[/tex] como sendo o conjunto [tex]G(f)=\{(x,f(x))~|~ x\in A\}[/tex], ou seja, o conjunto de todos os pares ordenados [tex](x,y)[/tex] tais que [tex]x\in A[/tex] e [tex]y = f(x)[/tex].
Particularmente o que, de fato, interessa no estudo de uma função [tex]f[/tex] não é propriamente o conjunto [tex]G(f)[/tex], mas sim a representação dos pares ordenados [tex](x,f(x))[/tex] em um plano cartesiano.
Pela definição apresentada acima, [tex]G(f) = \{(x,f(x))~|~ x\in \mathbb{R}\} = \{(x,x+1)~|~ x\in \mathbb{R}\}[/tex].
Vamos construir uma tabela a fim de determinarmos alguns dos pontos desse gráfico.
[tex]\begin {array}{|c| c| c|}
\hline
x & f(x)=x+1 & (x,f(x)) \\
\hline
-2,5 & -2,5+1 = -1,5 & (-2,5; -1,5) \\
\hline
-2 & -2+1 = -1 & (-2;~ -1) \\
\hline
-1,5 & -1,5+1 = -0,5 & (-1,5; -0,5) \\
\hline
-1 & -1+1 = 0 & (-1;~ 0) \\
\hline
-0,5 & -0,5+1 = 0,5 & (-0,5; 0,5) \\
\hline
0 & 0+1 = 1 & (0;~ 1) \\
\hline
0,5 & 0,5+1 = 1,5 & (0,5; 1,5) \\
\hline
1 & 1+1 = 2 & (1;~ 2) \\
\hline
1,5 & 1,5+1 = 2,5 & (1,5; 2,5) \\
\hline
\end{array}[/tex]
Geometricamente, podemos representar os pontos do gráfico em um plano cartesiano.
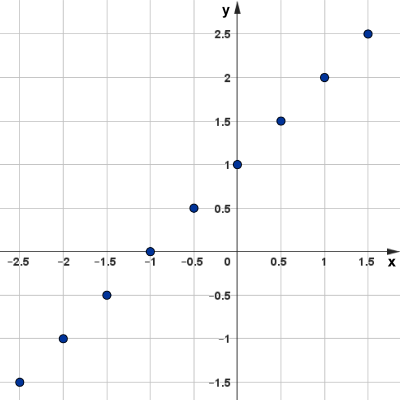
Como podemos perceber, os nove pontos marcados no plano cartesiano estão alinhados, o que nos leva a acreditar que o gráfico da função é uma reta. Ou seja, independente de qual valor colocamos para [tex]x[/tex], vamos encontrar um par ordenado [tex](x,f(x))[/tex] que está alinhado com os demais pontos já encontrados.
Mais à frente vamos estudar alguns tipos de funções que têm como gráfico uma reta.
Assim, traçando a reta que passa pelos pontos encontrados, temos o gráfico da função [tex]f[/tex]:
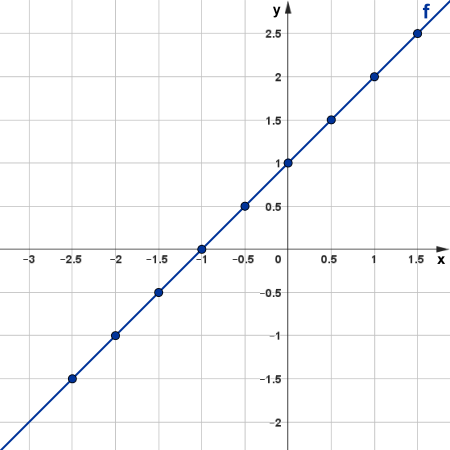
Exemplo 2: Consideremos a área [tex]A(l)[/tex] de um quadrado em função da medida [tex]l[/tex] de seu lado, ou seja, [tex]A(l) = l^2[/tex]. Restringindo a medida do lado desse quadrado no intervalo [tex]\left[\dfrac{1}{2}\, ,\, 2\right][/tex], como a área é um número real, então podemos representar a área pela função [tex]A:\left[\dfrac{1}{2}\, ,\, 2\right]\rightarrow \mathbb{R}[/tex] tal que [tex]A(l) = l^2[/tex]. Assim, o gráfico de [tex]A[/tex] é o conjunto
[tex]\qquad G(A) = \left\{(l,l^2)~|~ l\in \left[\dfrac{1}{2}\, ,\, 2\right]\right\}[/tex].
Também mais adiante, veremos como representar o conjunto de pontos [tex]\left(l,l^2\right)[/tex] em um plano cartesiano. Por enquanto apenas apresentaremos a curva!
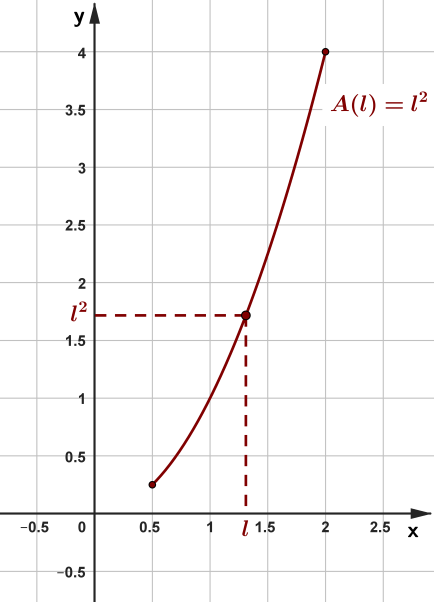
Muitas vezes podemos pensar no gráfico de uma função como sendo o rastro deixado por um ponto de coordenadas [tex](x,y)[/tex], quando a variável [tex]x[/tex] varia da esquerda para a direita, e a variável [tex]y[/tex] se move para cima ou para baixo, podendo, até mesmo, se manter estável em um valor fixo.
– Humm…
Então qualquer trajetória de um ponto móvel no plano cartesiano é gráfico de alguma função?

A resposta para essa pergunta é “Não!”. Veja a explicação a seguir.
Suponha que os pontos de coordenadas [tex](a,b)[/tex] e [tex](a,c),[/tex] com [tex]b\neq c,[/tex] pertençam ao gráfico de uma determinada função [tex]g[/tex]. Isso implicaria, pela definição de gráfico vista acima, que:
● [tex]a\in D(g)[/tex] e [tex]b = g(a),[/tex]
● [tex]a\in D(g)[/tex] e [tex]c = g(a);[/tex]
mas isso feriria gravemente o conceito de função, uma vez que a suposta função [tex]g[/tex] estaria fazendo corresponder dois valores diferentes ([tex]b[/tex] e [tex]c[/tex]) para uma mesma variável dependente [tex]a[/tex].
Para obtermos uma resposta rápida se uma curva é, ou não, gráfico de uma função, podemos utilizar o teste da reta vertical.
Exemplo 1: A curva abaixo representa o gráfico de uma função, pois qualquer reta perpendicular ao eixo [tex]x[/tex] intersecta a curva num único ponto, como podemos observar particularmente nas retas que aparecem na figura.
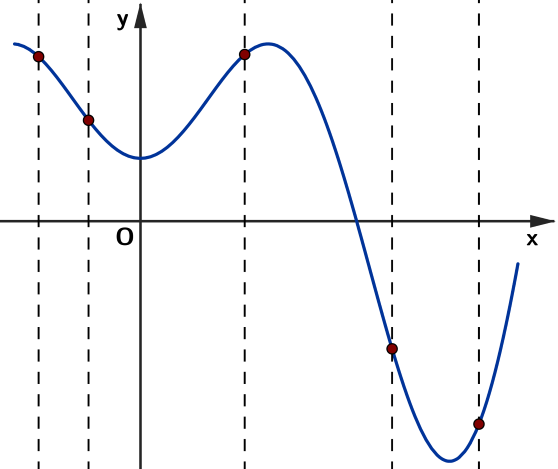
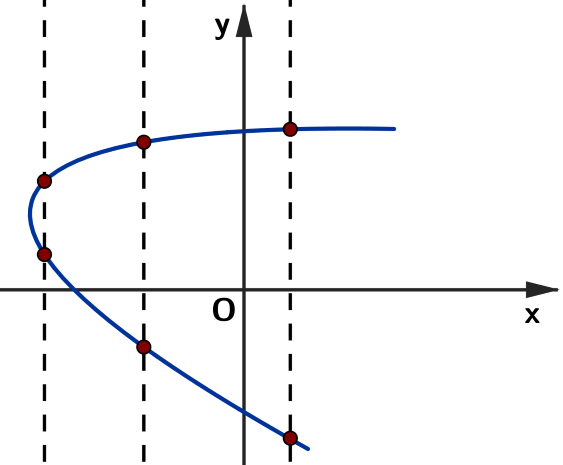
Exemplo 2: A curva abaixo não representa o gráfico de uma função, uma vez que existem retas verticais que cortam a curva em mais de um ponto, como as mostradas na imagem.
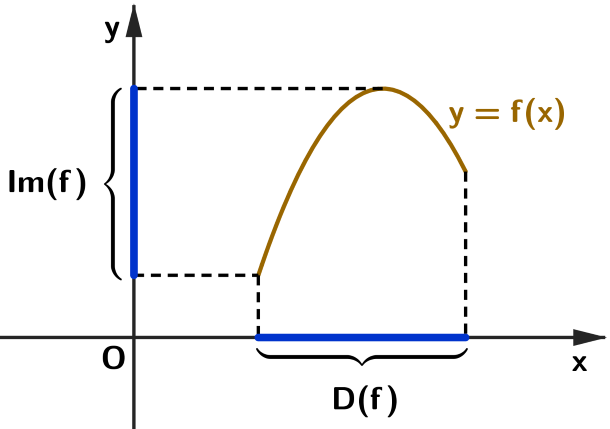
Tendo o gráfico [tex]G(f)[/tex] de uma função [tex]f[/tex] qualquer, é possível determinar qual o domínio [tex]D(f)[/tex] e qual a imagem [tex]Im(f)[/tex] da mesma. Para isso, basta que façamos a projeção do gráfico sobre cada um dos eixos coordenados [tex]Ox[/tex] e [tex]Oy[/tex]:
► o domínio [tex]D(f)[/tex] é a projeção de [tex]G(f)[/tex] sobre o eixo das abscissas;
► a imagem [tex]Im(f)[/tex] é a projeção de [tex]G(f)[/tex] sobre o eixo das ordenadas;
conforme ilustra a figura a seguir.
É importante ressaltarmos que nem todos os gráficos de funções são vistos necessariamente como uma única curva. Podem existir funções cujos gráficos são compostos por duas ou mais curvas, bem como gráficos compostos apenas por pontos isolados, como veremos no próximo exemplo.
Solução: Como fizemos no último exemplo, vamos atribuir valores para [tex]x[/tex] a fim de obtermos alguns pontos do gráfico. É importante observarmos que, como o domínio da função [tex]g[/tex] é o conjunto [tex]\mathbb{N}[/tex], então só podemos atribuir a [tex]x[/tex] números naturais. Veja a tabela:
[tex]\begin {array}{|c| c| c|}
\hline
x & g(x)=-x+5 & (x,g(x)) \\
\hline
0 & -0+5 = 5 & (0,~ 5) \\
\hline
1 & -1+5 = 4 & (1,~ 4) \\
\hline
2 & -2+5 = 3 & (2,~ 3) \\
\hline
3 & -3+5 = 2 & (3,~ 2) \\
\hline
4 & -4+5 = 1 & (4,~ 1) \\
\hline
5 & -5+5 = 0 & (5,~ 0) \\
\hline
6 & -6+5 = -1 & (6,~ -1) \\
\hline
7 & -7+5 = -2 & (7,~ -2) \\
\hline
\end{array}[/tex]
Destacando no plano cartesiano os pontos encontrados, temos:
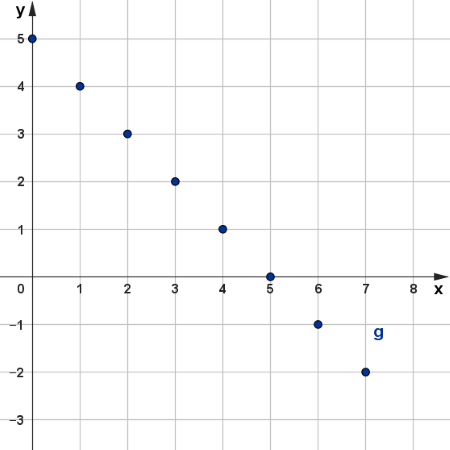
Você deve ter percebido que os pontos neste outro exemplo também estão alinhados e talvez possa estar se perguntando se iremos traçar a reta para determinar o gráfico da função, não é mesmo? No entanto, neste exemplo não podemos traçar nenhuma curva. Veja que se traçássemos a reta que passa por pontos afirmando ser ela o gráfico da função [tex]g[/tex], estaríamos considerando, por exemplo, que o ponto [tex](1,5;~3,5)[/tex] pertence ao gráfico da função (uma vez que ele estaria sobre a reta), mas isso não é verdade, pois [tex]1,5[/tex] sequer pertence ao domínio da função ([tex]\mathbb{N}[/tex]).
Assim, o gráfico da função [tex]g[/tex] é, realmente, apenas o conjunto dos pontos isolados [tex](x, -x+5)[/tex], tal que [tex]x\in \mathbb{N}[/tex], conforme o gráfico acima.
Obviamente, tal gráfico é um conjunto infinito de pontos, mas como é impossível representar todos na imagem, consideramos apenas a representação de alguns. Note que, embora o ponto de coordenadas [tex](8,-3)[/tex] não esteja destacado, ele pertence ao gráfico da função, mas [tex](-1,6)[/tex] não pertence ao gráfico, pois [tex]-1\notin \mathbb{N}[/tex].
A seguir temos um exemplo de função em que o gráfico é composto por duas curvas. (Isso mesmo, duas curvas! Matematicamente falando, retas e semirretas são exemplos de curvas…)
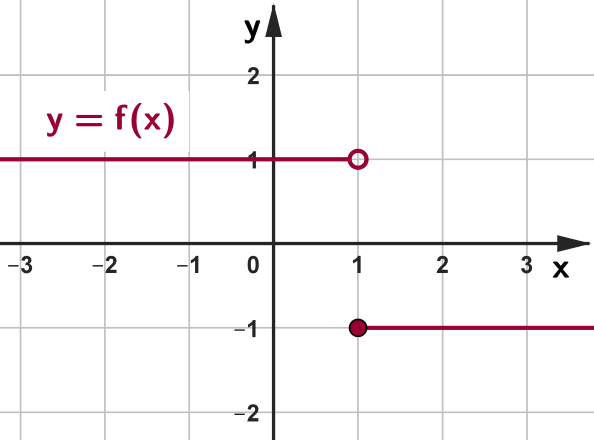
Você deve estar se perguntando porque o gráfico acima tem uma bolinha preenchida e uma em branco, não é mesmo?
Bom, como vimos um pouco acima, cada ponto do plano cartesiano tem suas coordenadas representadas como um par ordenado. Essas bolinhas trazem algumas informações acerca do domínio e imagem da função: o ponto representado pela bolinha colorida pertence ao gráfico [tex]G(f)[/tex], enquanto que o ponto representado pela bolinha em branco (não preenchida) não pertence ao gráfico [tex]G(f)[/tex] da função [tex]f[/tex].
Assim, a função cujo gráfico está representado acima é [tex]f:\mathbb{R}\rightarrow \{-1,1\}[/tex] dada por
[tex]\qquad f(x) = \begin{cases}1, \text{ se } x\lt 1\\
-1, \text{ se } x\geq 1\end{cases}.[/tex]
Observação: A função acima definida é um exemplo de função em que a lei de formação é definida por duas ou mais regras.
Podemos obter algumas informações importantes sobre o comportamento de uma função observando o seu gráfico.
No próximo tópico veremos como!
Analisando gráficos de funções
Observando o gráfico de uma função, podemos visualizar geometricamente algumas características importantes dessa função. Vamos apresentar a seguir alguns elementos e algumas propriedades que o gráfico de uma função pode mostrar.
Raízes de uma função
Chamamos de raiz da função [tex]f[/tex] (ou zero da função [tex]f[/tex]) a todo elemento [tex]a\in A, [/tex] tal que [tex]f(a) = 0.[/tex]
Exemplo 1: O número [tex]-\dfrac{1}{2}[/tex] é raiz da função [tex]f: \mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x) = 2x+1[/tex], pois [tex]f\left(-\dfrac{1}{2}\right) = 2\cdot \left(-\dfrac{1}{2}\right)+1 = 0[/tex].
Exemplo 2: Os números [tex]-1[/tex] e [tex]1[/tex] são raízes da função [tex]g: \mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x) = x^2-1[/tex], pois [tex]g(-1) = g(1) = 0[/tex].
Graficamente, a raiz de uma função pode ser entendida como o número obtido na interseção do gráfico da função com o eixo das abcissas.
Assim, por exemplo, considerando a função do primeiro exemplo visto na seção de gráficos ([tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] definida por [tex]f(x) = x+1[/tex]), como o ponto de interseção do gráfico com o eixo das abcissas é o ponto de coordenadas [tex](-1,0)[/tex], podemos afirmar que [tex]-1[/tex] é a raiz da função. De fato,
[tex]\qquad f(x) = 0\iff x+1=0 \iff \boxed{x = -1}.[/tex]
Veremos, mais adiante, que nem todas as funções possuem raízes no conjunto dos números reais.
Função Par e Função Ímpar
Exemplo: A função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x) = x^2[/tex] é par, pois [tex]f(-x)=(-x)^2 = x^2 = f(x)[/tex], para todo [tex]x\in\mathbb{R}[/tex].
Mas o que significa, geometricamente, uma função ser par?
Vejamos.
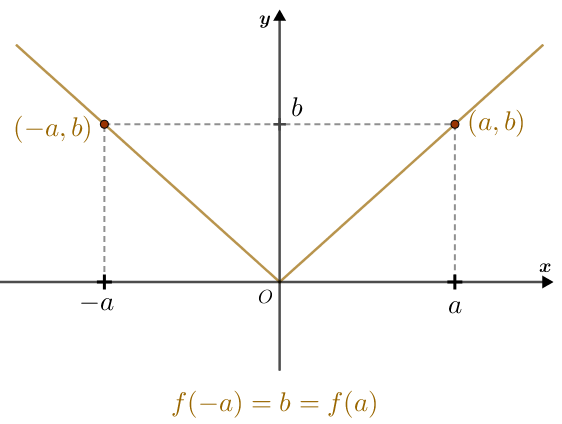
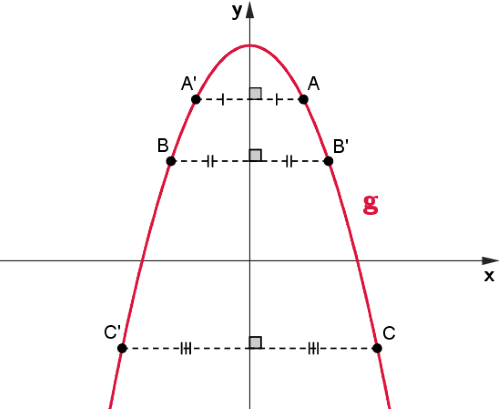
Se uma dada função [tex]f[/tex] é par, então, por definição, para cada ponto [tex]x[/tex] no domínio de [tex]f[/tex], tem-se [tex]f(-x) = f(x)[/tex], o que implica que, sendo [tex]y = f(x)[/tex], os pontos [tex](-x,y)[/tex] e [tex](x,y)[/tex] pertencem ao gráfico de [tex]f[/tex].
Mas, conforme visto anteriormente no segundo caso de simetria de pontos no plano cartesiano, os pontos [tex](-x,y)[/tex] e [tex](x,y)[/tex] são simétricos com relação ao eixo [tex]y[/tex]. Dessa forma, como [tex]x[/tex] é um ponto genérico do domínio da função, conclui-se que o gráfico de uma função par no plano cartesiano é uma curva simétrica com relação ao eixo [tex]y[/tex].
Exemplo: A função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x) = x^3[/tex] é ímpar, pois [tex]f(-x)=(-x)^3 = -x^3 =-f(x)[/tex], para todo [tex]x\in\mathbb{R}[/tex].
Vejamos o que significa, geometricamente, uma função ser ímpar.
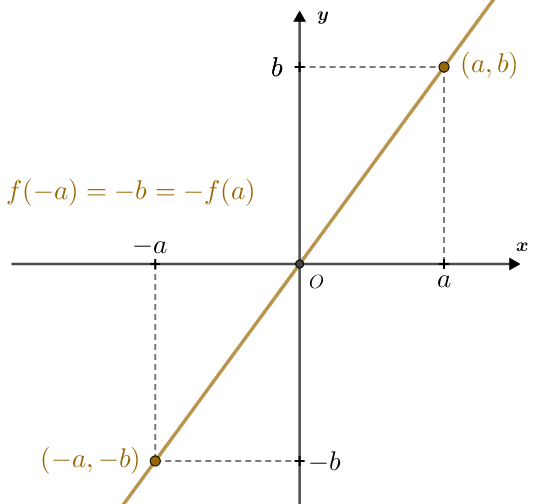
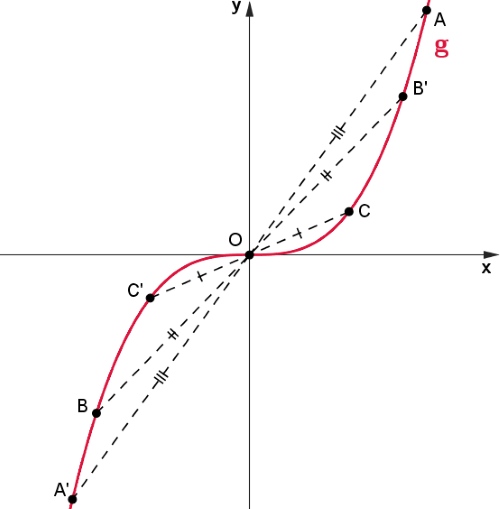
Se uma função [tex]f[/tex] é ímpar, então, para cada ponto [tex]x[/tex] no domínio de [tex]f[/tex], tem-se [tex]f(-x)=-f(x)[/tex], o que implica que, sendo [tex]y = f(x)[/tex], os pontos [tex](-x,-y)[/tex] e [tex](x,y)[/tex] pertencem ao gráfico de [tex]f[/tex], além, também, de eles serem simétricos com relação à origem [tex]O[/tex] do plano cartesiano, conforme visto anteriormente no terceiro caso de simetria de pontos no plano cartesiano. Como [tex]x[/tex] é um ponto genérico no domínio da função, conclui-se que o gráfico de uma função ímpar no plano cartesiano é uma curva simétrica com relação à origem.
Observações importantes:
(1) Considere a função [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x) = x^2+x.[/tex]
Observe que [tex]h(1) = 1[/tex] e [tex]h(-1)=0[/tex]. Dessa forma temos que:
[tex]\qquad h(-1)\ne h(1)[/tex], logo [tex]h[/tex] não é par.
[tex]\qquad h(-1)\ne- h(1)[/tex], logo [tex]h[/tex] não é ímpar.
Portanto, existem funções que não são pares e nem ímpares.
(2) Considere a função [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x)=0.[/tex]
Agora, observe que para qualquer número real [tex]x[/tex], temos que [tex]g(x)=0[/tex] e [tex]g(-x)=0[/tex]. Assim:
[tex]\qquad g(x)=g(-x)[/tex] e, portanto, [tex]g[/tex] é uma função par.
[tex]\qquad g(x)=0=-0=-g(-x)[/tex] e, portanto, [tex]g[/tex] é uma função ímpar.
Portanto, existem funções que são pares e ímpares ao mesmo tempo.
Na verdade, a lei de formação [tex]g(x)=0[/tex] é a única que permite definir funções simultaneamente pares e ímpares.
Função Crescente e Função Decrescente
Crescimento e decrescimento são conceitos fundamentais no aprendizado de funções matemáticas. Quando vamos analisar o comportamento de uma função, é importante entender, além de outros fatores, se a variável dependente aumenta ou diminui conforme a variável independente muda.
Graficamente, temos o seguinte esquema:
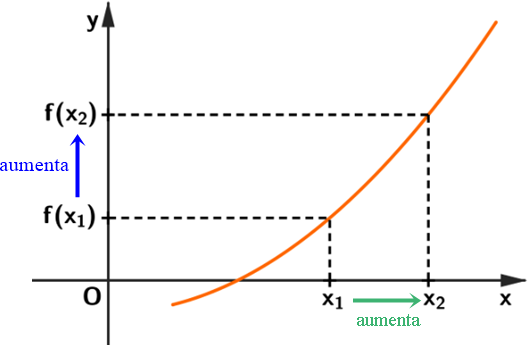
Graficamente, temos este esquema:
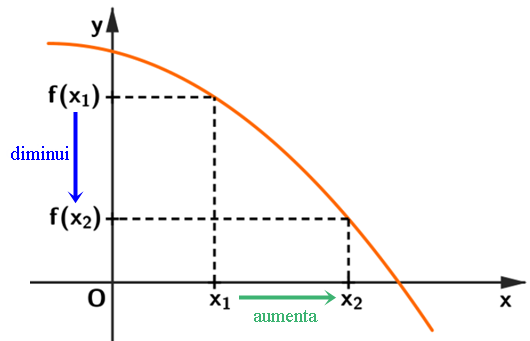
De fato, dados [tex]x_1, x_2\in \mathbb{R}[/tex], com [tex]\boxed{x_1\lt x_2}[/tex], temos que:
[tex]\qquad f(x_1) = x_1^3 \lt x_2^3 = f(x_2).[/tex]
Assim, [tex]\boxed{f(x_1) \lt f(x_2)}[/tex] e [tex]f[/tex] é uma função crescente.
Exemplo 2: A função [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x) = -x[/tex] é decrescente.
Observe que se [tex]x_1, x_2\in \mathbb{R}[/tex] com [tex]\boxed{x_1\lt x_2}[/tex], então
[tex]\qquad g(x_1) = -x_1 \gt -x_2 = g(x_2).[/tex]
Com isso, [tex] \boxed{g(x_1) \gt g(x_2)}[/tex] e, portanto, [tex]g[/tex] é uma função decrescente .
Exemplo 3: Quanto à função [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x) = sen \;x[/tex], veja que [tex]0, \dfrac{\pi}{2}, \dfrac{3\pi}{2}\in D(h)[/tex].
Temos que:
[tex]\qquad \boxed{0\lt \dfrac{\pi}{2}}[/tex] e [tex]h(0) = sen \;0 = 0\lt 1 = sen \;\dfrac{\pi}{2} = h\left(\dfrac{\pi}{2}\right)[/tex],
logo [tex] \boxed{h(0)\lt h\left(\frac{\pi}{2}\right)}[/tex].
Por outro lado, temos
[tex]\qquad \boxed{0\lt \dfrac{3\pi}{2}}[/tex] e [tex]h(0) = sen \;0 = 0\gt -1 = sen \;\dfrac{3\pi}{2} = h\left(\dfrac{3\pi}{2}\right)[/tex],
logo [tex]\boxed{h(0)\gt h\left(\frac{3\pi}{2}\right)}[/tex].
Dessa forma, em alguns pontos, [tex]h[/tex] satisfaz a condição de ser crescente; mas, em outros, satisfaz a condição de ser decrescente. Logo [tex]h[/tex] não é crescente, nem decrescente.
Conforme vimos no Exemplo 3, existem funções que não são nem crescentes e nem decrescentes; no entanto, funções desse tipo podem ter regiões de crescimento e regiões de decrescimento, conforme podemos observar na figura abaixo.
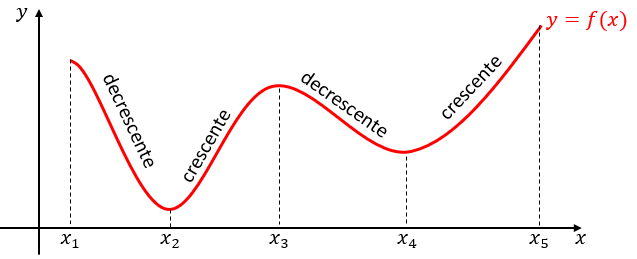
Perceba que:
► [tex]f[/tex] é crescente para valores de [tex]x[/tex] de [tex]x_2[/tex] a [tex]x_3[/tex] e de [tex]x_4[/tex] a [tex]x_5;[/tex]
► [tex]f[/tex] é decrescente para valores de [tex]x[/tex] de [tex]x_1[/tex] a [tex]x_2[/tex] e de [tex]x_3[/tex] a [tex]x_4.[/tex]
Se você quiser trabalhar um pouquinho mais com gráficos de funções, clique no botão abaixo.
Como já estabelecemos uma linguagem inicial e algumas propriedades básicas sobre funções, vamos aprofundar um pouco a nossa discussão.
Para isso, vamos apresentar três novas Salas: duas com assuntos específicos e uma terceira com problemas e vídeos.
➤ Sala 2: Alguns tipos de funções.
➤ Sala 3: Problemas.
Recomendamos fortemente que vocês continuem a leitura seguindo a ordem na qual essas Salas estão anunciadas.
Vamos lá?
| Sala 1 | Sala 2 | Sala 3 |
Equipe COM – OBMEP
Novembro de 2023.
[1] IEZZI G.; DOLCE O.; DEGENSZAJN D.; PÉRIGO R.; ALMEIDA N. Matemática – ciências e aplicações 1: conecte live. São Paulo: Saraiva, 2018.
[2] IEZZI G.; DOLCE O.; DEGENSZAJN D.; PÉRIGO R.; ALMEIDA N. Matemática: volume único. São Paulo: Atual, 1997.
[3] IEZZI, Gelson. MURAKAMI, Carlos. Fundamentos de matemática elementar, 1: conjuntos, funções. 10. ed. São Paulo: Atual, 2013.
[4] IEZZI, Gelson. DOLCE Osvaldo. MURAKAMI, Carlos. Fundamentos de matemática elementar, 2: logaritmos. 10. ed. São Paulo: Atual, 2013.
[5] Portal da Matemática
