✏ Link da Sala para dispositivos da Apple.
Nesta Sala vamos tentar visualizar propriedades características de funções olhando apenas para os seus respectivos gráficos!
 Vamos lá!
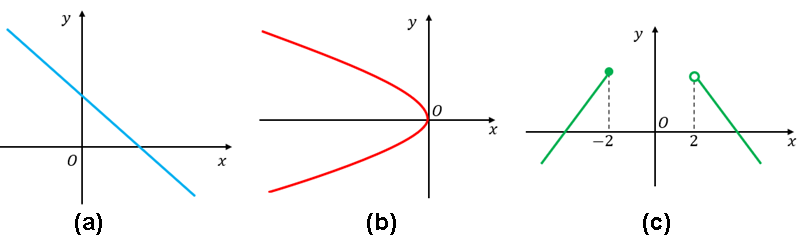
Vamos lá!(a) Sim. E podemos até considerar que o Domínio e o Contradomínio da função, digamos, [tex]f[/tex] é o conjunto dos números reais. Assim, teríamos o gráfico de uma função [tex]f:\mathbb{R} \rightarrow \mathbb{R}[/tex].
(b) Não. Observe que temos números reais negativos com duas imagens. Na figura a seguir, vemos a representação gráfica de três desses números (pontos).
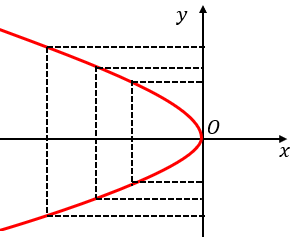
(c) Depende. Se considerarmos como domínio o conjunto dos números reais, a curva que aparece neste item não é gráfico de uma função, visto que qualquer número real pertencente ao intervalo [tex]]-2,2][/tex] não teria imagem.
Mas se considerarmos como domínio a união dos conjuntos [tex]\{x \in \mathbb{R}~|~x \leqslant 2\}~[/tex] e [tex]~\{x \in \mathbb{R}~|~x \gt2\}~[/tex], aí teremos um gráfico de função:
[tex]\qquad g:\{x \in \mathbb{R}~|~x \leqslant 2\} \cup \{x \in \mathbb{R}~|~x \gt2\} \rightarrow \mathbb{R}[/tex].
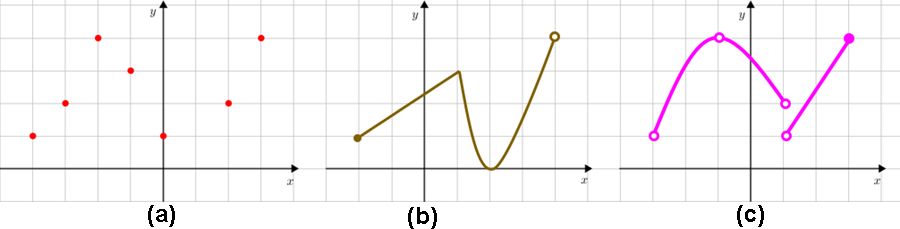
Sejam [tex]f[/tex], [tex]g[/tex] e [tex]h[/tex] as funções cujos gráficos aparecem nas imagens acima. Assim:
(a) [tex]D(f)=\{-4,-3,-2,-1,0,2,3\}.[/tex]
(b) [tex]D(g)=[-2,4\,[=\{x \in \mathbb{R}~|-2 \leqslant x \lt 4\}.[/tex]
(c) [tex]D(h)=\,]-3,3]-\{-1,1 \}\\
D(h)=\{x \in \mathbb{R}~|-3 \lt x \leqslant 3\text{, com } x \ne -1\text{ e } x\ne 1\}.[/tex]
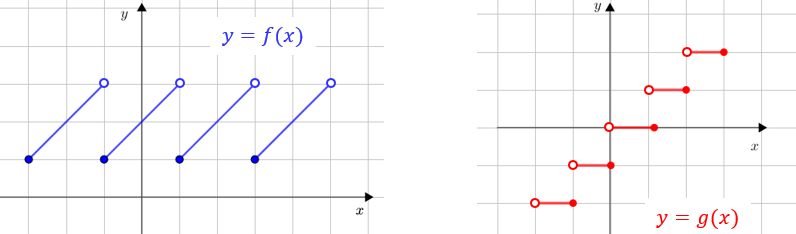
[tex]\quad \begin{align*}
\textcolor{blue}{D(f)=\{x \in \mathbb{R}~|~-3\leqslant x \lt 5\}} \qquad & \textcolor{red}{D(g)=\{x \in \mathbb{R}~|~-2\lt x \leqslant 3\}}\\
\textcolor{blue}{Im(f)=\{y \in \mathbb{R}~|~1\leqslant y \lt 3\}} ~~~~\qquad & \textcolor{red}{Im(g)=\{-2,-1,0,1,2\}}\\
\end{align*}
[/tex]
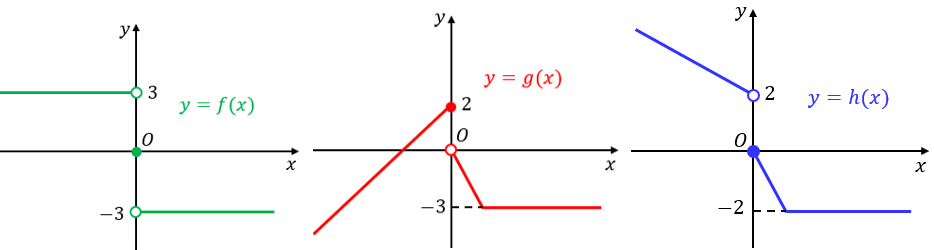
[tex]\qquad \textcolor{#00B050}{Im(f)=\{-3,0,3\}.} \\
\qquad \textcolor{red}{Im(g)=\{y \in \mathbb{R}~|~y\leqslant 2\}.} \\
\qquad \textcolor{blue}{Im(h)=\{y \in \mathbb{R}~|y \gt 2\}\cup \{y \in \mathbb{R}~|-2 \leqslant y \leqslant 0\}.}\\[/tex]

[tex]\qquad \textcolor{#FF33CC}{Im(k)=\{y \in \mathbb{R}~|~ -2 \leqslant y\leqslant 2\}.} \\
\qquad \textcolor{#BF9000}{Im(t)=\{y \in \mathbb{R}~|~y\leqslant 2 \text{ ou } y=3\}.}[/tex]
a)
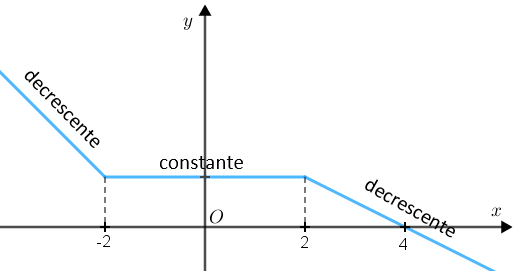
► Decrescente nos intervalos [tex]\{x \in \mathbb{R}~|~ x \leqslant -2\}~[/tex] e [tex]~\{x \in \mathbb{R}~|~ x \geqslant 2\}.[/tex]
► Constante no intervalo [tex]\{x \in \mathbb{R}~|-2 \leqslant x \leqslant 2\}.[/tex]
b) 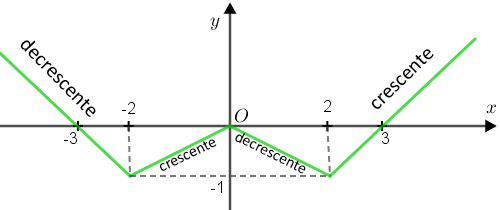
► Decrescente nos intervalos [tex]\{x \in \mathbb{R}~|~ x \leqslant -2\}~[/tex] e [tex]\{x \in \mathbb{R}~|~ 0 \leqslant x \leqslant 2\}.[/tex]
► Crescente nos intervalos [tex]\{x \in \mathbb{R}~|~-2 \leqslant x \leqslant 0\}~[/tex] e [tex]\{x \in \mathbb{R}~| x \geqslant 2\}.[/tex]
c) 
►Crescente nos intervalos [tex]\{x \in \mathbb{R}~|~ x \lt 0\}~[/tex] e [tex]~\{x \in \mathbb{R}~|~ x \geqslant 0\}.[/tex]
Como [tex]\{x \in \mathbb{R}~|~ x \lt 0\}~\cup ~\{x \in \mathbb{R}~|~ x \geqslant 0\}=\mathbb{R}[/tex], podemos dizer que a função é crescente?
Representando o gráfico de [tex]f[/tex] em linha cheia e o de [tex]g[/tex] em linha tracejada, a figura que melhor se ajusta a esses dados é:
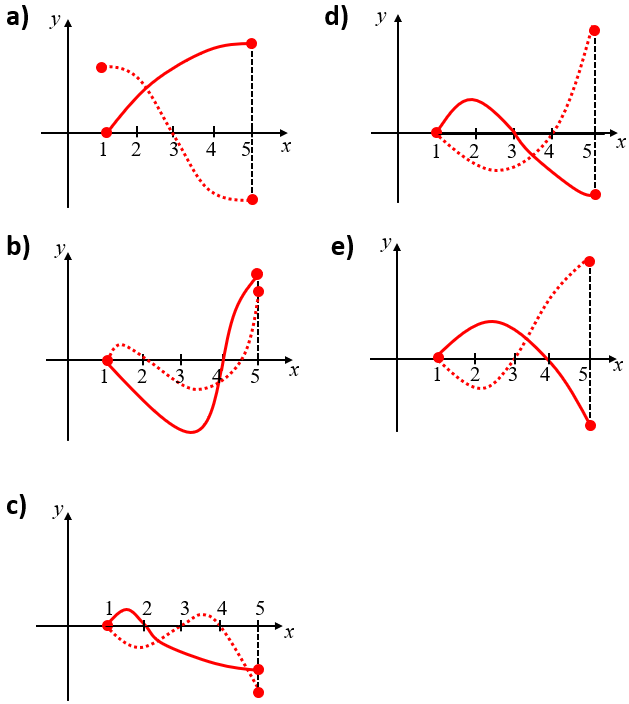
► Na figura a, observe que [tex]g(1) \gt 0 [/tex], logo [tex]g(1) \ne 0.[/tex] Assim a condição de que [tex]g(1)=0[/tex] não está cumprida e podemos eliminar esta figura.
► Observando a figura b, percebemos que [tex]3[/tex] não é raiz de nenhuma das duas funções e, portanto, teríamos [tex]f(3)\ne 0~[/tex] e [tex]~g(3)\ne 0.[/tex]
No entanto, sabemos que [tex]f(3) \cdot g(3)=0[/tex], logo devemos ter [tex]f(3)=0[/tex] ou [tex]g(3) =0[/tex]. Portanto, também podemos eliminar esta figura.
► Observe que tanto na figura d quanto na figura e temos que a imagem [tex]g(5)[/tex] é positiva e a imagem [tex]f(5)[/tex] é negativa e, com isso, temos [tex]g(5) \gt f(5)[/tex], o que contraria a informação de que [tex]f(5) \gt g(5).[/tex]
Dessa forma eliminamos simultaneamente essas duas figuras.
► Observe que na figura c todas as condições apresentadas no problema são cumpridas: [tex]f(1) = g(1) = 0[/tex], [tex]g(3)=0~[/tex] e [tex]f(5) \gt g(5).[/tex]
Portanto, a figura que melhor se ajusta aos dados do problema é a figura c.
a) Responda se cada item abaixo é verdadeiro ou falso.
(i) [tex] f(-2)=f(2)[/tex]
(ii) A função [tex]f[/tex] possui exatamente uma raiz real.
b) Aproveite e analise o crescimento e decrescimento da função.
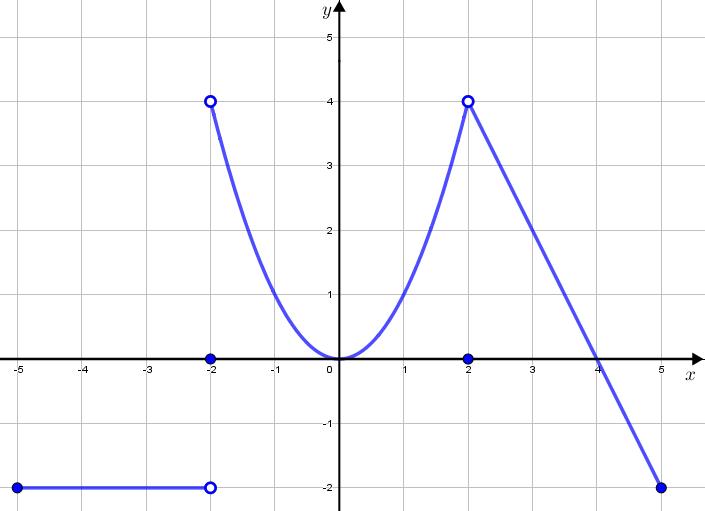
a)
Portanto, [tex]f(-2)=f(2)= 0 [/tex] e este item é verdadeiro.
(ii) Veja que o gráfico de [tex]f[/tex] corta o eixo das abscissas nos pontos [tex](-2,0),(0,0),(2,0),(4,0)[/tex] (pontos azuis sobre o eixo das abscissas, conforme indicado na figura a seguir).
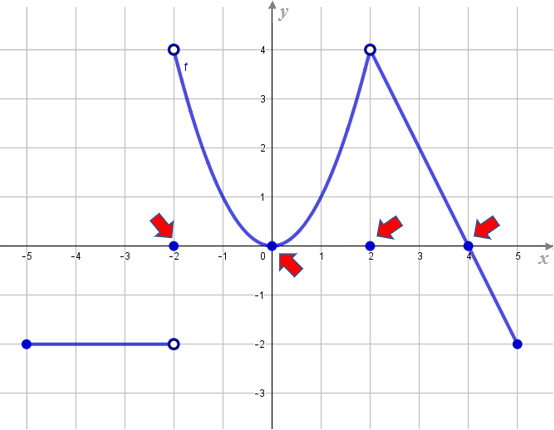
Assim, [tex]f(-2)=0 \, [/tex], [tex]f(0)=0 \, [/tex], [tex]f(2)=0 \, [/tex], [tex]f(4)=0 \, [/tex] e, portanto, a função [tex]f[/tex] possui quatro raízes: [tex]-2[/tex], [tex]2[/tex], [tex]0[/tex] e [tex]4[/tex].
Pelo exposto, este item é falso!
b) ► [tex]f[/tex] é constante no intervalo [tex]\{x \in \mathbb{R}~|-5 \leqslant x \lt -2\}.[/tex]
► [tex]f[/tex] é crescente no intervalo [tex]\{x \in \mathbb{R}~|~0 \leqslant x \lt 2\}.[/tex]
► [tex]f[/tex] é decrescente nos intervalos [tex]\{x \in \mathbb{R}~|~-2 \lt x \leqslant 0\}~[/tex] e [tex]~\{x \in \mathbb{R}~|~2 \lt x \leqslant 5\}.[/tex]
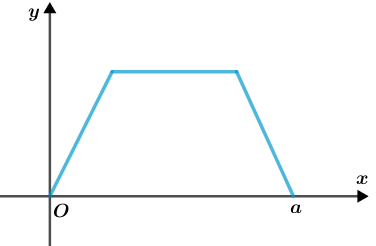
A partir desse gráfico, é possível construirmos o gráfico de uma função [tex]g:[-a,a]\rightarrow \mathbb{R}[/tex] de modo que [tex]g[/tex] seja par?
E para que [tex]g[/tex] seja ímpar?
a) Observe que o gráfico abaixo define uma função par de [tex][-a,a][/tex] em [tex]\mathbb{R}.[/tex]
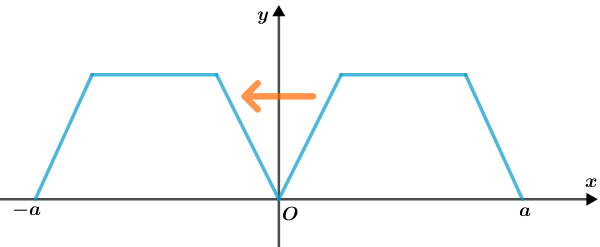
b) Observe, agora, que o gráfico abaixo define uma função ímpar de [tex][-a,a][/tex] em [tex]\mathbb{R}.[/tex]

c) Para as duas funções definidas, determine graficamente as regiões de crescimento e decrescimento.



a) A curva apresentada no item a não representa o gráfico de uma função, já que existem retas verticais que cortam a curva em mais de um ponto. Observe na próxima imagem as retas [tex]~r~[/tex] e [tex]~s.[/tex]

b) A curva apresentada no item b também não representa o gráfico de uma função. Observe na figura abaixo que as retas verticais [tex]~t~[/tex] e [tex]~v[/tex] cortam a curva em dois pontos cada uma.

c) A curva apresentada no item c não representa o gráfico de uma função. Observe que se a curva em questão fosse o gráfico de uma função, [tex]x=4[/tex] teria várias imagens. Na figura abaixo sinalizamos quatro dessas imagens.
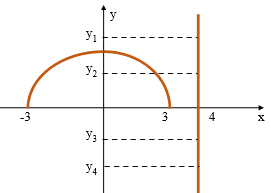
Equipe COM – OBMEP
