✏ Link da Sala para dispositivos da Apple.
Nesta Sala vamos tentar encontrar, se possível, funções escondidas em tabelas, relações e fórmulas em cada exemplo a seguir.
Vamos definir a seguinte relação [tex]R[/tex] entre os elementos de [tex]A[/tex] e de [tex]B[/tex]:
se [tex]x \in A[/tex] vamos relacioná-lo com o elemento [tex]y \in B[/tex] tal que [tex] y^2=4-x^2.[/tex]
Vamos verificar se essa relação [tex]R[/tex] define uma função
[tex]\qquad \begin{eqnarray*}
A &\rightarrow & B\\
x&\mapsto & y
\end{eqnarray*}[/tex].
Para isso, temos que verificar se a relação [tex] y^2=4-x^2[/tex] é tal que para cada [tex]x\in A[/tex] ela define um único [tex]y\in B.[/tex]
Vamos lá!
► Se [tex]x=2[/tex], segue que o [tex]y[/tex] correspondente é tal que

[tex] \qquad y^2=4-2^2\\
\qquad y^2=4-4=0\\
\qquad y=0.[/tex]
► Se [tex]x=-2[/tex], segue que o [tex]y[/tex] correspondente é tal que
[tex] \qquad y^2=4-(-2)^2\\
\qquad y^2=4-4=0\\
\qquad y=0.[/tex]
► Se [tex]x=0[/tex], segue que o [tex]y[/tex] correspondente é tal que
[tex] \qquad y^2=4-0^2\\
\qquad y^2=4-0=4\\
\qquad y=2\text{ ou } y=-2.[/tex]
O diagrama mostra que a relação em questão não define uma função, pois ao elemento [tex]0[/tex] de [tex]A[/tex] temos dois valores associados em [tex] B[/tex]: [tex] 2~[/tex] e [tex]-2.[/tex]
Esta é a relação: [tex]R=\{(-2,0),(2,0),(0,2),(0,-2)\}.[/tex]
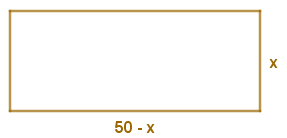
a) Mudando o valor de x, o perímetro P do retângulo correspondente muda?
Vamos inicialmente ver o que acontece com o perímetro para alguns valores particulares de x:
| x | 1 cm | 2 cm | 3 cm | 4 cm | 5 cm |
| P | 100 cm | 100 cm | 100 cm | 100 cm | 100 cm |
Para os valores de x escolhidos, não houve alteração do perímetro. E isso acontece para qualquer valor de x:
P = x + (50 – x) + x + (50 – x) = 50 + 50 = 100 cm.
Observe que o perímetro não é função do valor de x escolhido, pois ele é sempre 100; mas, mesmo assim, podemos definir uma função para modelar a situação. Para essa função o domínio pode ser definido, por exemplo, por todos os números reais positivos menores do que 50, e o contradomínio é qualquer conjunto que contenha o número 100; veja um exemplo:
[tex]\qquad \qquad P:\{ x\in \mathbb{R}~|~0 \lt x \lt 50\}\rightarrow \{100\}\\
\qquad \qquad~\qquad \qquad P(x)=100.[/tex]
(Como as imagens são todas iguais a 100, essa função é denominada uma função constante.)
b) E com relação à área, mudando o valor de x, a área A do retângulo correspondente muda?
Vamos ver o que acontece com a área para alguns valores particulares de x:
| x | 1 cm | 2 cm | 3 cm | 4 cm | 5 cm |
| A | 49 cm² | 96 cm² | 141 cm² | 184 cm² | 225 cm² |
Temos alguma função escondida nesta situação?
Observe que se x é um número real positivo menor do que 50, podemos calcular a área A do retângulo correspondente da seguinte maneira:
[tex] \qquad \qquad A=x\cdot(50-x)\\
\qquad \qquad \boxed{A=50x-x^2}.[/tex]
Assim, a partir dessa fórmula, podemos definir uma função [tex]A[/tex] que nos fornece a área de qualquer retângulo definido pela figura, tomando o contradomínio mais “cômodo” possível:
[tex]\qquad \qquad A:\{ x\in \mathbb{R}~|~0 \lt x \lt 50\}\rightarrow\mathbb{R}\\
\qquad \qquad~\qquad \quad A(x)=50x-x^2.[/tex]
Qual seria o conjunto imagem para a função [tex]A[/tex]?
► Seu Antonio resolveu fazer uma promoção em sua lojinha e se propôs vender xícaras a preços bem camaradas. Para os fregueses não terem que ficar fazendo continhas para saberem quantas xícaras poderiam levar com o dinheiro que cada um tinha na sua carteira, fez um cartaz bem grande e colocou pertinho da prateleira onde estavam as xícaras.
| Quantidade de xícaras | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Preço total em reais | 3,20 | 6,40 | 9,60 | 12,80 | 16,00 | 19,20 | 22,40 | 25,60 | 28,80 | 32,00 |
► Julinho resolveu esvaziar uma piscina inflável que ele tem em casa. Para contribuir com o meio ambiente, ele resolveu reutilizar a água para lavar o seu carro e as calçadas, armazenando-a em tambores com tampa. Então, ele colocou uma das pontas de uma mangueira na saída de água da piscina e a outra ponta no local onde a água iria ser despejada e, durante os dez primeiros minutos, percebeu a vazão da água mostrada na tabela abaixo.
| Tempo, em minutos | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Quantidade de litros | 3,2 | 6,4 | 9,6 | 12,8 | 16 | 19,2 | 22,4 | 25,6 | 28,80 | 32 |
Se [tex]x[/tex] representa a quantidade de xícaras que um freguês da lojinha de seu Antonio vai comprar, então o valor em reais a ser pago por esse freguês é dado por [tex]3,2x[/tex]; por outro lado, a quantidade de água armazenada pelo Julinho em [tex]x[/tex] minutos também pode ser expressa por [tex]3,2x[/tex]. Mas as funções que traduzem as duas situações apresentadas não são a mesma, embora ambas tenham a mesma lei de formação.
Isso acontece porque a quantidade de xícaras de uma compra é um número natural (ninguém vai comprar uma xícara e meia, por exemplo); mas podemos questionar qual a quantidade de água recolhida em 2,5 minutos de vazão, não é?
Assim, a função que define a compra de xícaras tem como domínio um subconjunto dos números naturais; por sua vez, o domínio da função que modela o problema do recolhimento de água é um conjunto formado por números reais.
Por exemplo, se a quantidade de xícaras por compra fosse limitada a 30 e a quantidade de água a ser armazenada em cada tambor fosse 30 litros teríamos duas funções distintas para modelar as duas situações:
►Valor [tex]V[/tex] em reais pagos por uma compra de [tex]x[/tex] xícaras:
[tex]\qquad \qquad V:\{ 0,1,2,\cdots,30\}\rightarrow \mathbb{R}\\
\qquad \qquad~\qquad V(x)=3,2x.[/tex]
►Quantidade [tex]Q[/tex] de litros água no tambor, após uma vazão de [tex]x[/tex] minutos:
[tex]\qquad \qquad Q:\{ x\in \mathbb{R}~|~0 \leq x \leq 30\}\rightarrow \mathbb{R}\\
\qquad \qquad~\qquad \quad Q(x)=3,2x.[/tex]

Como é possível construir um retângulo formado com um número qualquer de quadrados, qual seria a função que descreve a quantidade de palitos necessários para se construir uma fileira de [tex]n[/tex] quadrados?
A tabela a seguir mostra a relação entre o número de quadrados de um retângulo e o número de palitos necessários para formá-lo.
| Número de quadrados | 1 | 2 | 3 | 4 | 5 | 6 |
| Número de palitos | 4 | 7 | 10 | 13 | 16 | 19 |
Dessa forma, a função [tex]h[/tex] que fornece o número de palitos necessários para formar [tex]n[/tex] quadrados pode ser assim definida:
[tex]\qquad \qquad h:\mathbb{N}^*\rightarrow \mathbb{N}\\
\qquad\quad h(n)=3n+1.[/tex]
O Climograma é uma ferramenta gráfica de representação do clima que permite uma análise das variações de temperatura e precipitações de uma região ao longo de um determinado período.
Ele é um gráfico duplo que resulta da junção de um gráfico de linha para as médias de temperatura e um gráfico de colunas para as médias de precipitação.

A relação entre as médias de temperatura e de precipitação registradas na simulação do Climograma acima define, de alguma forma, uma função?
► Inicialmente, observe que o índice de 70 mm de precipitação está associado a três temperaturas diferentes: 10°C; 15°C e 20°C.

► Observe também que a temperatura de 20°C está associada a dois índices de 70 mm de precipitação distintos: 70 mm e 80 mm.

Pelo exposto, não temos uma função definida “do conjunto das variações de precipitações no conjunto das variações de temperaturas” e nem “do conjunto das variações de temperaturas no conjunto das variações de precipitações”.
Se ela continuar com a mesma lei de formação, podemos observar sem grandes problemas que essa sequência define uma função [tex]F[/tex] cujo domínio é o conjunto dos números naturais não nulos, o contradomínio pode ser o conjunto dos números naturais e que a cada número natural [tex]n[/tex], [tex]n\ne 0[/tex], associa o número que ocupa a enésima posição na sequência. Mas essa função [tex]F[/tex] tem uma lei de formação?
A resposta é sim; essa função tem uma lei de formação. Mas ela é um pouco diferente; isso porque essa lei de formação não define pontualmente o valor [tex]F(m)[/tex] que ocupa a posição [tex]m[/tex] na sequência.
A lei de formação da função [tex]F[/tex] é o que chamamos de “fórmula de recursão ou recursiva”, já que você vai recorrer aos dois elementos imediatamente anteriores da sequência para definir um determinado termo:
[tex]\qquad \qquad \begin {cases}F(1)=F(2)=1\\
F(n + 2) = F(n + 1) + F(n), \text{ para } n \geq 1\end{cases}[/tex]
ou seja, repetimos o número [tex]1[/tex] duas vezes e, a partir do terceiro termo, somamos os dois termos imediatamente anteriores a ele.
Se você não sabe como surgiu essa sequência, assista a este vídeo.
Aqui também temos uma sequência que, se continuar com a mesma lei de formação, vai definir uma função [tex]T[/tex] cujo domínio é [tex]\mathbb{N}^*[/tex], conjunto dos números naturais não nulos. O contradomínio pode ser o conjunto dos números naturais e a função é tal que a cada número natural não nulo [tex]n[/tex] associa o número que ocupa a enésima posição nela.
Essa função [tex]T[/tex] tem uma lei de formação que pode ser definida recursivamente a partir do segundo termo, fazendo [tex]T(1)=1[/tex]; observe:
[tex]\qquad \boxed{T(2)=T(1)+2=1+2=3}; \\
\qquad \boxed{T(3)=T(2)+3=3+3=6};\\
\qquad \boxed{T(4)=T(3)+4=6+4=10};\\
\qquad \boxed{T(5)=T(4)+5=10+5=15};\\
\qquad \boxed{T(6)=T(5)+6=15+6=21} \cdots [/tex]
Assim, temos:
[tex]\qquad \qquad \begin {cases}T(1)=1\\
T(n)=T(n-1) + n, \text{ para } n \geq 2.\end{cases}[/tex]
Observe que :
[tex]T(2)=T(1)+2=1+2\\
T(3)=T(2)+3=1+2+3\\
T(4)=T(3)+4=1+2+3+4\\
T(5)=T(4)+5=1+2+3+4+5\\
\qquad \qquad \dots[/tex]
Assim, [tex] T(n)=1+2+3+4+5+\cdots+n=\dfrac{(n+1)\cdot n}{2}.[/tex]
Para conhecer um pouco melhor essa sequência, visite esta Sala.
Essa relação define uma função de [tex]A[/tex] em [tex]B[/tex]?
Observe que:
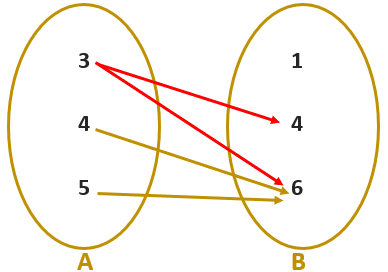
► O único elemento de [tex]B[/tex] que está relacionado com [tex]x=5[/tex] é o [tex]6[/tex], pois [tex]5 \lt 6[/tex], mas [tex]5 \gt 4[/tex] e [tex]5 \gt 1.[/tex]
► O único elemento de [tex]B[/tex] que está relacionado com [tex]x=4[/tex] é o [tex]6[/tex], pois [tex]4 \lt 6[/tex], mas [tex]4=4[/tex] e [tex]4 \gt 1.[/tex]
► Já o elemento [tex]x=3[/tex] de [tex]A[/tex] está relacionado com [tex]6[/tex] e [tex]4[/tex] mas não está relacionado com [tex]1[/tex], já que [tex]3 \lt 6[/tex], [tex]3 \lt 4[/tex] e [tex]3 \gt 1.[/tex]
O diagrama ao lado mostra que a relação em questão não define uma função de [tex]A[/tex] em [tex]B[/tex], pois ao elemento [tex]3[/tex] de [tex]A[/tex] temos dois valores associados em [tex] B[/tex]: [tex]4~[/tex] e [tex]~6.[/tex]
Essa relação define uma função de [tex]E[/tex] em [tex]F[/tex]?
Observe que:
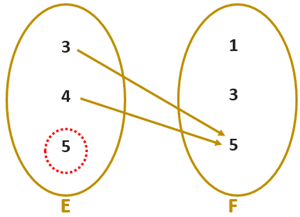
► O único elemento de [tex]F[/tex] que está relacionado com [tex]x=3[/tex] é o [tex]5[/tex], pois [tex]3 \lt 5[/tex], mas [tex]3=3[/tex] e [tex]3 \gt 1.[/tex]
► O único elemento de [tex]F[/tex] que está relacionado com [tex]x=4[/tex] é o [tex]5[/tex], pois [tex]4 \lt 5[/tex], mas [tex]4\gt 3[/tex] e [tex]4 \gt 1.[/tex]
► Nenhum elemento de [tex]F[/tex] está relacionado com [tex]5[/tex], pois [tex]5 \gt 1[/tex], [tex]5 \gt 3[/tex] e [tex]5=5.[/tex]
Essa relação também não define uma função de [tex]E[/tex] em [tex]F[/tex], pois não existe elemento em [tex]F[/tex] relacionado com [tex]x=5[/tex].
Equipe COM – OBMEP
