Permutações Circulares e os
Números de Stirling do primeiro tipo
O tema principal que desenvolveremos nesta Sala, Números de Stirling do primeiro tipo, não é um assunto abordado no Ensino Médio. Entretanto, é um tema muito conveniente para o Projeto dos Clubes de Matemática, por se tratar de um problema geral de contagem que, quando considerado em um caso particular, incide no conceito de Permutação Circular. Pelo fato de envolver contagem de configurações discretas e tratar-se de um problema de contagem, é possível trabalhar esse tema no Ensino Médio, mais especificamente no segundo ano, quando for abordado o estudo de sequências numéricas e análise combinatória ou quando da apresentação da definição de permutação circular.
Na Matemática, existe também o conceito de Números de Stirling do segundo tipo que, embora também esteja associado a um problema de contagem, não será explorado aqui. Deixamos apenas como tema para pesquisa ou por curiosidade dentro do Projeto dos Clubes de Matemática da OBMEP.
Nesta sala, faremos um breve estudo sobre os números de Stirling do primeiro tipo, que definem uma sequência numérica cujos termos estão relacionados a alguns interessantes problemas de contagem. Vamos basear a nossa discussão em um problema de contagem que está diretamente relacionado com esses números e é um exemplo particular do conceito de permutações circulares.
Bons Estudos, pessoal!
Quem foi Stirling?
James Stirling foi um matemático escocês que contribuiu com avanços importantes na teoria das séries infinitas e no cálculo infinitesimal. Ele nasceu em 11 de maio de 1692 em Garden, Reino Unido. Pouco se sabe sobre sua formação acadêmica além de que em 1710 ele viajou para Oxford e se matriculou no Balliol College Oxford, no início de 1711. A família de Stirling apoiava fortemente a causa jacobita (Veja a referência [13].) e isso teria uma influência significativa na sua vida.
Em 1717, publicou seu primeiro trabalho, Lineae Tertii Ordinis Neutonianae, em Oxford. Nesse trabalho, Stirling estendeu a teoria de Newton para curvas planas de grau 3, adicionando mais 4 tipos de curvas às 72 estudadas por Newton. Nesse livro, encontra-se também o problema da trajetória ortogonal que foi levantado por Leibniz e estudado por outros matemáticos como, por exemplo, Johann Bernoulli e Euler. Stirling resolveu o problema no início de 1716.
Em 1724, Stirling viajou para Londres e lá permaneceu por dez anos. Nesse período, manteve contato com vários matemáticos (De Moivre, Euler, Gabriel Cramer, Maclaurin, entre outros) e deu aula na William Watt’s Academy. Em 1730 publicou seu trabalho mais importante: Methodus Differentialis.
Stirling retornou à Escócia em 1735, quando foi nomeado gerente da “empresa de mineração escocesa Leadhills”, em Lanarkshire. Em 1745, Stirling publicou um artigo sobre a ventilação dos poços de minas; mas, provavelmente, não desistiu da Matemática. Há relatos dele sobre seus trabalhos matemáticos que foram escritos entre 1730 e 1745 e não foram publicados.
Stirling morreu no dia 5 de dezembro de 1770, em Edimburgo, Reino Unido.

Imagens extraídas de Wikipedia
Para saber mais sobre a vida do matemático James Stirling, clique AQUI e acesse um texto do site do MacTutor, um recurso on-line que contém biografias de quase 3000 matemáticos!
Permutação Circular
Segue do Princípio Multiplicativo que há [tex]\,\fcolorbox{black}{#e8e8e8}{$n!$}\,[/tex] sequências ordenadas de [tex]n[/tex] objetos, ou seja, [tex]n![/tex] maneiras de permutar [tex]n[/tex] objetos. (Para mais detalhes visite esta Sala para Leitura do nosso Blog.)
Vejamos um exemplo.
Figura 1: Contas para formar uma pulseira
► De quantas maneiras podemos permutar os símbolos exibidos na Figura 1?
A resposta para a questão é [tex]4!=24[/tex] e, para ilustrar, listaremos todas as [tex]24[/tex] permutações. Para facilitar, vamos rotular cada um destes símbolos com as letras [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex], como segue na tabela.
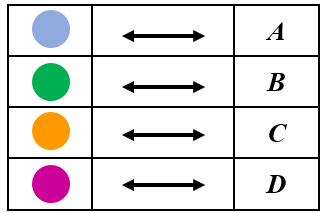
Figura 2: Contas associadas às letras [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex] D[/tex].
As [tex]24[/tex] permutações escritas na forma de sequências são:
[tex](A, B, C, D)\,;\,(B, C, D, A)\,;\,(C, D, A, B)\,;\,(D, A, B, C);[/tex]
[tex](A, C, B, D)\,;\,(C, B, D, A)\,;\,(B, D, A, C)\,;\,(D, A, C, B);[/tex]
[tex](A, C, D, B)\,;\,(C, D, B, A)\,;\,(D, B, A, C)\,;\,(B, A, C, D);[/tex]
[tex](A, B, D, C)\,;\,(B, D, C, A)\,;\,(D, C, A, B)\,;\,(C, A, B, D);[/tex]
[tex] (A, D, B, C)\,;\,(D, B, C, A)\,;\,(B, C, A, D)\,;\,(C, A, D, B);[/tex]
[tex](A, D, C, B)\,;\,(D, C, B, A)\,;\,(C, B, A, D)\,;\,(B, A, D, C).[/tex]
Agora vamos considerar a seguinte questão:
► Com os símbolos [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex] D[/tex] representando contas que podem ser utilizadas na confecção de pulseiras, quantas pulseiras podem ser feitas usando essas quatro contas?
Para efeito de contagem, vamos considerar que as pulseiras formadas foram colocadas sobre uma mesa, para que não consideremos que essas pulseiras sejam viradas e que sejam feitos outros movimentos com elas, que não o de girá-las sobre a mesa.
Observe que, nessas condições, são seis as pulseiras formadas:
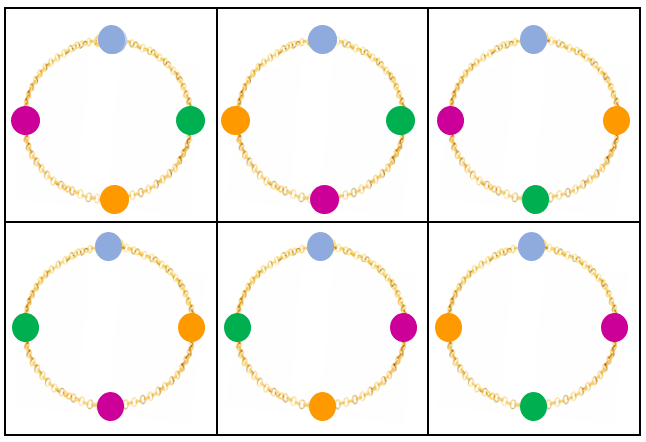
Figura 3: As seis pulseiras distintas formadas pelas [tex]4[/tex] contas.
Vamos considerar a primeira pulseira mostrada na Figura 3 e vamos girá-la no sentido anti-horário, de forma que a conta verde ocupe o lugar da conta azul. A seguir, giramos novamente no sentido anti-horário (segundo giro), mudando novamente a posição da conta verde para a nova posição da conta azul, e assim sucessivamente. Note que a pulseira é a mesma e que as posições das contas voltarão para a posição inicial, se fizermos o quarto giro.
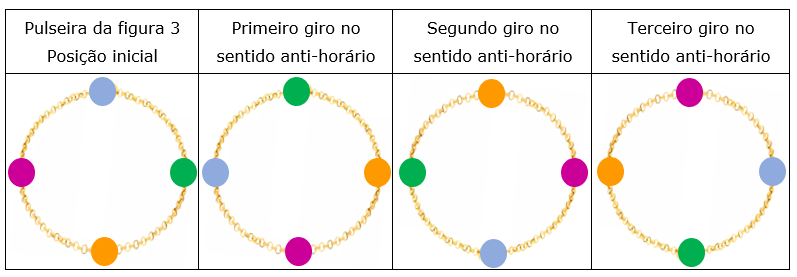
Figura 4: Giros da pulseira no sentido anti-horário.
Observe que podemos associar cada uma das seis pulseiras da Figura 3 a um círculo no qual são dispostas as letras [tex] A, B, C[/tex] e [tex]D[/tex] que correspondem às contas com que formamos as pulseiras. Na figura a seguir, descrevemos o círculo associado à primeira pulseira.
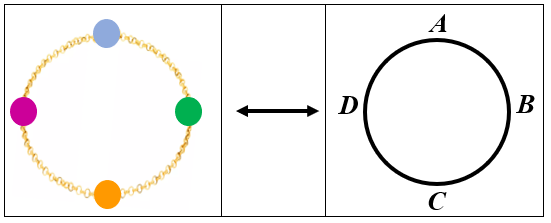
Figura 5: Pulseira associada a uma distribuição circular das letras [tex]A,B,C,D[/tex].
Vamos reescrever o problema das pulseiras…
Inicialmente, veja que, por exemplo, [tex] (A, B, C, D); (B, C, D, A); (C, D, A, B); (D, A, B, C) [/tex] representam a mesma pulseira, pois basta girarmos uma delas no sentido horário que obtemos as demais.
Note que as permutações [tex] (A, C, B, D); (C, B, D, A); (B, D, A, C); (D, A, C, B) [/tex] também representam as mesmas pulseiras.
Observamos, então, que temos seis pulseiras distintas e, a partir delas, podemos gerar todas as permutações dos quatro símbolos que fizemos anteriormente. Para isso, veja a ilustração a seguir, que corresponde à lista de todas as permutações de quatro objetos descritas no exemplo.
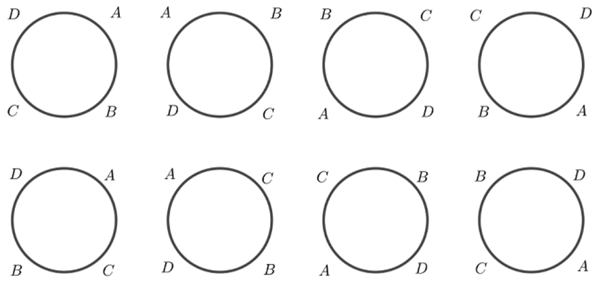
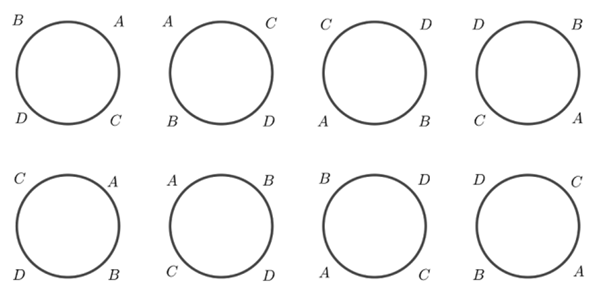
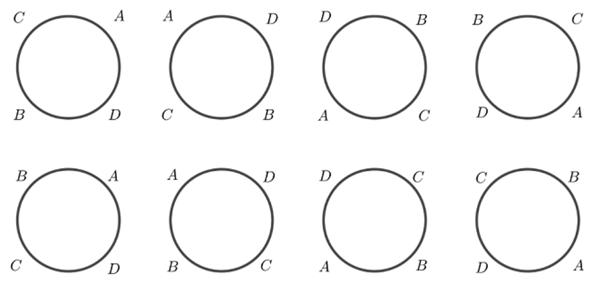
Figura 6: Distribuição das permutações de quatro objetos em torno do círculo.
Assim, podemos distribuir as quatro contas [tex]A, B, C[/tex] e [tex]D[/tex] ao longo de uma pulseira de [tex]24[/tex] maneiras; no entanto, essas [tex]24[/tex] distribuições definem apenas [tex]6[/tex] pulseiras, digamos, diferentes.
Olhando o problema das pulseiras numa perspectiva mais geral, o que pretendemos agora é contar o número de maneiras de se ordenar [tex]n[/tex] objetos em torno de um círculo.
Para isso, vamos estabelecer o conceito de permutação circular, que consiste em ordenar [tex]n[/tex] objetos em um círculo.
No Exemplo 2 vocês devem ter percebido que para cada permutação circular de [tex]4[/tex] objetos geramos [tex]4[/tex] sequências formadas pelos mesmos objetos (veja Figura 6). Dessa forma, para esse exemplo, o total de permutações circulares é [tex] \dfrac{4!}{4} = \dfrac{4 \cdot 3!}{4}=3!=(4-1)!. [/tex]
Vamos denotar por [tex]PC_{n}[/tex] o total de permutações circulares de [tex]n[/tex]. No exemplo anterior calculamos, então, [tex]PC_{4}=3!=6[/tex].
Generalizando esse caso particular, temos que o total de permutações circulares de [tex]n[/tex] objetos é [tex] PC_{n} = (n-1)![/tex]. Para obter essa fórmula, basta observar que, para cada permutação circular de [tex]n[/tex] objetos, podemos gerar sequências ordenadas de [tex]n[/tex] objetos, ou seja, [tex] n \cdot PC_{n} = n![/tex] e, então, [tex] PC_{n}= \dfrac{n!}{n} = \dfrac{n \cdot (n-1)!}{n} = (n-1)!.[/tex]
Assim:
O número de permutações circulares de [tex]n[/tex] objetos distintos é denotado por [tex]PC_{n}[/tex] e assim definido:
[tex]\qquad \qquad \fcolorbox{black}{#e8e8e8}{$ PC_{n} = (n-1)!$}\,[/tex].
Uma outra alternativa para estabelecer a quantidade de permutações circulares de [tex]n[/tex] objetos é observar que, em uma mesa circular com [tex]n[/tex] assentos com pessoas sentadas, não sabemos quem é o primeiro ou o último nessa configuração. Dessa forma, fixada uma pessoa nessa mesa para ser a primeira, podemos formar [tex](n-1)![/tex] filas com as pessoas restantes. Assim, da mesma forma, concluímos que [tex] PC_{n}=(n-1)![/tex].
Antes de apresentarmos os Números de Stirling,
que tal algumas atividades envolvendo Permutação Circular?
a) De quantas maneiras distintas [tex] 7 [/tex] crianças podem dar as mãos para brincar de ciranda?
b) De quantas maneiras distintas [tex] 7 [/tex] crianças podem dar as mãos para brincar de ciranda, sendo que as crianças [tex]A[/tex] e [tex]B[/tex] fiquem lado a lado?
Números de Stirling do primeiro tipo
Considere o seguinte problema de contagem:
- Pessoa [tex]A [/tex] senta-se sozinha. Pessoas [tex]B,C[/tex] e [tex]D [/tex] sentam-se juntas.
- Pessoa [tex]A [/tex] senta-se sozinha. Pessoas [tex] B,D[/tex] e [tex] C [/tex] sentam-se juntas.
- Pessoa [tex] B [/tex] senta-se sozinha. Pessoas [tex]A,D[/tex] e [tex] C [/tex] sentam-se juntas;
- Pessoa [tex] B [/tex] senta-se sozinha. Pessoas [tex]A,C[/tex] e [tex] D [/tex] sentam-se juntas;
- Pessoa [tex] C [/tex] senta-se sozinha. Pessoas [tex]A,B[/tex] e [tex] D [/tex] sentam-se juntas;
- Pessoa [tex] C [/tex] senta-se sozinha. Pessoas [tex]B,A[/tex] e [tex] D [/tex] sentam-se juntas;
- Pessoa [tex] D [/tex] senta-se sozinha. Pessoas [tex] A,B[/tex] e [tex] C [/tex] sentam-se juntas;
- Pessoa [tex] D [/tex] senta-se sozinha. Pessoas [tex] A, C[/tex] e [tex] B [/tex] sentam-se juntas;
- Pessoas [tex]A [/tex] e [tex] B [/tex] sentam-se numa mesa e pessoas as [tex] C[/tex] e [tex] D [/tex] sentam-se na outra. (Ilustramos tal distribuição na figura 9.)
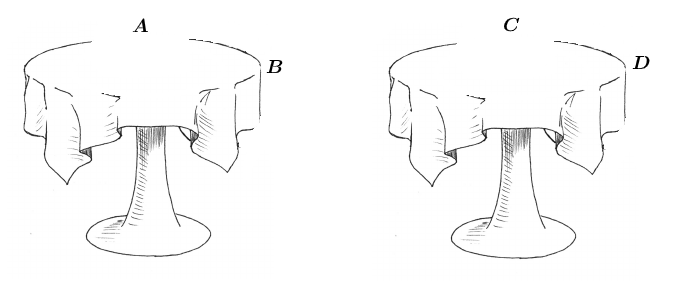
Figura 9:Ilustração com duas pessoas em cada mesa.Para os casos a seguir, a respectiva ilustração pode ser feita analogamente à figura [tex]9[/tex]:
- Pessoas [tex] A [/tex] e [tex] C [/tex] sentam-se numa mesa. Pessoas [tex] B [/tex] e [tex] D [/tex] sentam-se em outra;
- Pessoas [tex] A [/tex] e [tex] D[/tex] sentam-se numa mesa. Pessoas [tex] B[/tex] e [tex] C [/tex] sentam-se em outra.
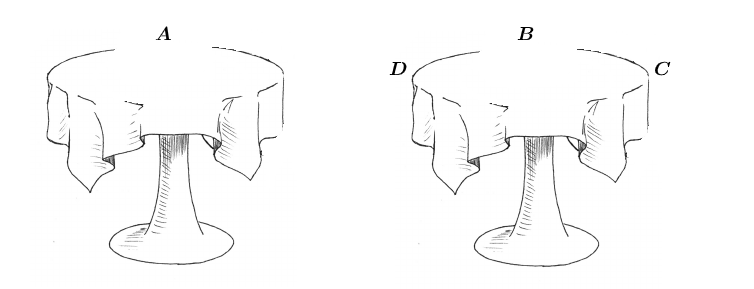
Figura 7: Ilustração da primeira distribuição nas mesas.
Observe que essa nova distribuição é simétrica à anterior.
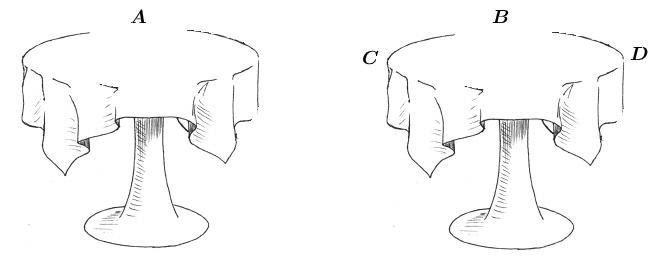
Figura 8:Ilustração da segunda distribuição nas mesas.
Para os casos listados a seguir a ilustração por meio dos desenhos são análogas às figuras [tex]7[/tex] e [tex] 8 [/tex]:
Logo, há [tex] 11[/tex] maneiras de distribuirmos as quatro pessoas em duas mesas circulares de forma que não fiquem mesas vazias.
Queremos agora observar a Questão 1 numa perspectiva mais geral, distribuindo [tex]n[/tex] pessoas em [tex]k[/tex] mesas circulares.
[tex]\qquad \textcolor{#4178a1}{(i)}[/tex] [tex]D(n, k)[/tex] o conjunto formado pelas distribuições de [tex]n[/tex] pessoas em [tex]k[/tex] mesas circulares idênticas sem que nenhuma fique vazia.
[tex]\qquad \textcolor{#4178a1}{(ii)}[/tex][tex] {\left[ \begin{array}{c} n \\ k \end{array} \right]} [/tex] o número de elementos do conjunto [tex]D(n,k)[/tex]. (Da Questão 1 segue, por exemplo, que [tex] {\left[ \begin{array}{c} 4 \\2 \end{array} \right]} =11 \,.[/tex])
Vamos fazer algumas análises iniciais de casos particulares da questão:
- Pelo enunciado, [tex]n[/tex] e [tex]k[/tex] são números que representam quantidade de pessoas e mesas, respectivamente; assim, tais números são inteiros não negativos.
- Agora, se temos mesas ([tex]k \gt 0[/tex]) e não temos pessoas para distribuir entre as mesas, então não temos o que fazer e [tex] {\left[ \begin{array}{c} 0 \\ k \end{array} \right]} =0\,. [/tex]
- Por outro lado, se existirem pessoas para serem distribuídas entre as mesas e não existirem mesas, então não temos como distribuir as pessoas. Logo, para [tex]n \gt 0[/tex], [tex] {\left[ \begin{array}{c} n \\ 0 \end{array} \right]} =0\,. [/tex]
- Se temos [tex]n[/tex] pessoas para sentarem-se em [tex]n[/tex] mesas, sem que nenhuma mesa fique vazia, necessariamente uma pessoa deverá se sentar em cada uma das mesas. Então, para [tex]n \gt 0[/tex], [tex] {\left[ \begin{array}{c} n \\ n \end{array} \right]} =1 [/tex], uma vez que as mesas são indistinguíveis.
- Se [tex]0 \lt n \lt k[/tex], então [tex] {\left[ \begin{array}{c} n \\ k \end{array} \right]} =0 [/tex], já que é impossível fazermos a distribuição, pois não podemos ter mesas vazias e temos mais mesas do que pessoas.
Estabelecidas essas condições iniciais, a ideia agora é analisar o problema para [tex]n \gt k \gt 1[/tex] e estabelecer uma relação de recorrência. Para isso, vamos dividir o conjunto [tex] D(n,k)[/tex] em dois subconjuntos disjuntos. Assim, sejam [tex]p_{1}, p_{2} , \dots, p_{n}[/tex] as [tex] n[/tex] pessoas que iremos distribuir para sentarem-se nas [tex]k[/tex] mesas circulares idênticas, sem que não fiquem mesas vazias, e consideremos os seguintes conjuntos:
- Caso 1: O subconjunto de [tex]D(n,k)[/tex] formado pelas possíveis distribuições das pessoas [tex]p_{1}, p_{2} , \dots, p_{n}[/tex], de modo que a pessoa [tex] p_{n}[/tex] fique sozinha em uma mesa.
Observe que, como as mesas são indistinguíveis, tanto faz em que mesa ficará a pessoa que sentará sozinha; assim, o total de distribuições possíveis neste caso é o número de soluções para o problema de distribuir [tex]n-1[/tex] pessoas em [tex]k-1[/tex] mesas o que, por definição, é [tex] {\left[ \begin{array}{c} n -1\\ k-1 \end{array} \right]}[/tex]. - Caso 2: O subconjunto de [tex]D(n,k)[/tex] formado pelas possíveis distribuições das pessoas [tex]p_{1}, p_{2} , \dots, p_{n}[/tex], de maneira que a pessoa [tex] p_{n}[/tex] fique em uma mesa com mais de uma pessoa.
Precisamos determinar o total de elementos desse subconjunto de [tex]D(n,k)[/tex], como fizemos no caso anterior. - Perceba que temos um total de [tex] {\left[ \begin{array}{c} n -1\\ k \end{array} \right]} [/tex] maneiras de distribuirmos as [tex]n-1[/tex] pessoas nas [tex]k[/tex] mesas, respeitando as condições do problema.
- Em cada uma dessas distribuições temos que colocar a pessoa [tex]p_{n}[/tex] e observamos que há [tex]n-1[/tex] lugares para alocá-la em uma mesa, já que a pessoa [tex] p_{n}[/tex] deve ficar em uma mesa na qual já tenha uma pessoa.
Para determinarmos a quantidade de distribuições do Caso 2, vamos distribuir inicialmente as pessoas [tex] p_{1}, p_{2}, \dots, p_{n-1}[/tex] nas [tex]k[/tex] mesas, de modo que não fiquem mesas vazias, e, em seguida, vamos colocar a pessoa [tex] p_{n}[/tex] em uma das mesas.
Dessa forma, segue do Princípio Multiplicativo que há [tex](n-1)\cdot {\left[ \begin{array}{c} n -1\\ k \end{array} \right]} [/tex] maneiras de distribuirmos as pessoas [tex] p_{1}, p_{2}, \dots, p_{n} [/tex] nas [tex]k[/tex] mesas circulares idênticas de forma que a pessoa [tex]p_{n}[/tex] não fique sozinha na mesa.
Segue desses dois casos que o total de elementos de [tex]D(n,k)[/tex] é igual a [tex](n-1) {\left[ \begin{array}{c} n -1\\ k \end{array} \right]} + {\left[ \begin{array}{c} n -1\\ k-1 \end{array} \right]} [/tex], ou seja,
[tex] \fcolorbox{black}{#b8c7d9}{$ {\left[ \begin{array}{c} n \\ k \end{array} \right]} ={\left[ \begin{array}{c} n -1\\ k-1 \end{array} \right]} + (n-1) {\left[ \begin{array}{c} n -1\\ k \end{array} \right]} $}\, [/tex], se [tex]1 \lt k \lt n[/tex].
Os números que denotamos por [tex] {\left[ \begin{array}{c} n \\ k \end{array} \right]} [/tex] para resolvermos a Questão 2 é o que se define na Matemática como Números de Stirling do primeiro tipo.
Como indicamos na apresentação desta Sala, na Matemática definimos os números de Stirling de primeiro e segundo tipos. Os primeiros, conforme discutimos na Questão 2, estão relacionados à contagem do número de maneiras de colocarmos pessoas em torno de mesas circulares idênticas, sem que nenhuma fique vazia. Já os números de Stirling do segundo tipo aparecem quando resolvemos o problema de distribuirmos objetos distintos em recipientes idênticos, de modo que nenhum recipiente fique vazio. Se em um primeiro momento você achou que as duas situações são idênticas, observe que no primeiro caso temos uma permutação circular e, no segundo, uma permutação simples. Se essa observação não foi suficiente, calcule, então, de quantas maneiras podemos colocar quatro objetos distintos em duas caixas idênticas, de modo que nenhuma fique vazia, e compare a sua solução com a solução da Questão 1. Mas voltando aos números de Stirling do primeiro tipo, vamos defini-los formalmente a seguir.
Por questões teóricas, convenciona-se que [tex] {\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]}=1 \;[/tex] e [tex] \;{\left[ \begin{array}{c} 0 \\ k \end{array} \right]}=0 [/tex] para [tex]k \gt 0.[/tex]
Vejamos algumas propriedades importantes desse tipo de números. Algumas delas apareceram nas análises iniciais que fizemos ao resolver a Questão 2 e vamos repetir as respectivas justificativas.
Propriedade 1:
Para [tex]k=0[/tex] e [tex]n\gt 0[/tex], temos pessoas para serem distribuídas entre as mesas, mas não existem mesas; então não temos como distribuir as pessoas. Logo
[tex]\fcolorbox{black}{#e8e8e8}{${\left[ \begin{array}{c} n \\ 0 \end{array} \right]} =0$}\,[/tex], para [tex]n \gt 0\,[/tex].
Propriedade 2:
Para [tex]0 \lt n \lt k[/tex], temos pessoas e mesas, mas é impossível fazermos a distribuição, pois não podemos ter mesas vazias e temos mais mesas do que pessoas. Assim,
[tex]\fcolorbox{black}{#e8e8e8}{$ {\left[ \begin{array}{c} n \\ k \end{array} \right]} =0$}\,[/tex], para [tex]0 \lt n \lt k\,[/tex].
Propriedade 3:
No caso de [tex]n[/tex] ser um inteiro positivo qualquer, o número [tex] \left[ \begin{array}{c} n \\ n \end{array} \right][/tex] é o número de modos de distribuirmos [tex] n[/tex] pessoas em [tex]n[/tex] mesas, sem que nenhuma mesa fique vazia. Neste caso, necessariamente cada pessoa deverá sentar-se em cada uma das mesas; e como as mesas são indistinguíveis, segue que [tex] {\left[ \begin{array}{c} n \\ n \end{array} \right]} =1. [/tex] Assim, levando em conta que, por definição, [tex] {\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]}=1 \;[/tex],
[tex]\fcolorbox{black}{#e8e8e8}{$ {\left[ \begin{array}{c} n \\ n \end{array} \right]} =1 $}\,[/tex], para [tex]n \geqslant 0 \,[/tex].
Propriedade 4:
No caso de [tex]n[/tex] ser um inteiro positivo qualquer e [tex]k=1[/tex], então o número [tex] \left[ \begin{array}{c} n \\ 1 \end{array} \right][/tex] fornece a quantidade de maneiras de distribuirmos [tex] n[/tex] pessoas em apenas uma mesa circular. Perceba que este problema é um caso explícito de permutação circular e, dessa forma,
[tex]\fcolorbox{black}{#e8e8e8}{$\left[ \begin{array}{c} n \\ 1 \end{array} \right] =PC_{n} = (n-1)! $}\,[/tex], para [tex]n \gt 0[/tex].
Propriedade 5:
Esta é uma interessante identidade que relaciona os números de Stirling e os números binomiais; observe.
Suponha, inicialmente, que [tex]n[/tex] seja um número natural maior do que [tex]2[/tex] e observe que para posicionarmos [tex] n [/tex] pessoas em [tex]n-1[/tex] mesas circulares idênticas, sem que mesas fiquem vazias, podemos colocar, inicialmente, [tex]n-2 [/tex] pessoas sozinhas em [tex]n-2[/tex] mesas e, em seguida, colocar as duas pessoas que sobraram na única mesa que restou.
Dessa forma, o problema consiste em escolher dentre as [tex] n[/tex] pessoas duas delas para sentarem-se juntas, que é igual a formar subconjuntos com [tex] 2[/tex] elementos de um conjunto com [tex]n[/tex] objetos, cujo total é [tex]{\left( \begin{array}{c} n \\ 2 \end{array} \right)} [/tex]. Logo, [tex] {\left[ \begin{array}{c} n \\ n-1 \end{array} \right]} ={\left( \begin{array}{c} n\\ 2 \end{array} \right)} [/tex].
Particularmente, se [tex]n=2[/tex], temos que:
- [tex] {\left[ \begin{array}{c} n \\ n-1 \end{array} \right]} = {\left[ \begin{array}{c} 2 \\ 1 \end{array} \right]}=(2-1)!=1 [/tex],
utilizando a Propriedade 4. - [tex] {\left( \begin{array}{c} n\\ 2 \end{array} \right)}={\left( \begin{array}{c} 2\\ 2 \end{array} \right)}=\dfrac{2!}{2! \cdot (2-2)!}=1 [/tex],
utilizando a definição de número binomial, [tex]{\left( \begin{array}{c} m\\ p \end{array} \right)}=\dfrac{m!}{p! \cdot (m-p)!}\,[/tex], e a convenção de que [tex]0!=1.[/tex]
Assim, se [tex]n=2[/tex], também vale a igualdade [tex] {\left[ \begin{array}{c} n \\ n-1 \end{array} \right]} ={\left( \begin{array}{c} n\\ 2 \end{array} \right)} [/tex] e, portanto:
[tex]\fcolorbox{black}{#e8e8e8}{${\left[ \begin{array}{c} n \\ n-1 \end{array} \right]} ={\left( \begin{array}{c} n\\ 2 \end{array} \right)} $}\,[/tex], para [tex]n \gt 1[/tex].
Propriedade 6:
Utilizando os Casos 1 e 2 da discussão da Questão 2, a seguinte relação de recorrência:
[tex]\fcolorbox{black}{#e8e8e8}{${\left[ \begin{array}{c} n \\ k \end{array} \right]} ={\left[ \begin{array}{c} n -1\\ k-1 \end{array} \right]} + (n-1) {\left[ \begin{array}{c} n -1\\ k \end{array} \right]}\,$}\,[/tex], para [tex] 1\lt k \lt n\,[/tex].
Para finalizar,
que tal mais algumas atividades?
(a) [tex] {\left[ \begin{array}{c} 3 \\ 2 \end{array} \right]}; \hspace {0.6cm}[/tex] (b) [tex] {\left[ \begin{array}{c} 4 \\ 2 \end{array} \right]}; \hspace{0.6cm} [/tex] (c) [tex] {\left[ \begin{array}{c} 4 \\3 \end{array} \right]} [/tex].
(a) [tex] {\left[ \begin{array}{c} 5 \\ 2 \end{array} \right]}, \hspace{0.6cm} [/tex] (b) [tex] {\left[ \begin{array}{c} 5 \\3 \end{array} \right]}, \hspace{0.6cm} [/tex] (c) [tex] {\left[ \begin{array}{c} 5 \\ 4 \end{array} \right]} [/tex].
- De quantas maneiras [tex] 6 [/tex] pessoas [tex]p_{1}, p_{2}, p_3, p_{4}, p_{5}, p_{6}[/tex] podem se sentar em [tex]3[/tex] mesas circulares idênticas, de forma que não fiquem mesas vazias?
Equipe COM – OBMEP
Agosto de 2020.
[1] BENJAMIN, A.T. J.J.Quinn. Proofs That Really Count: The Art of Combinatorial Proof. Mathematical Association of America, Washington, DC.2003
[2] GARCIA, Heitor Amaral. O ensino da análise combinatória através de situações problema. Monografia – UFMG, 2017.(Último acesso em 01/06/20)
[3] HAZZAM, S. Fundamentos de Matemática Elementar – Combinatória e Probabilidade, volume 4, 7 ed., editora atual, SP, 2004.
[4] MARINHO, JULIO CESAR DE SOUSA Demonstrações Combinatórias 2; orientador Michel Spira. Monografia – UFMG, 2006.
[5] SANTOS, J. P. O, MELLO M. P., MURARI I. T.C. Introdução à análise combinatória -3ed.- Campinas, SP: Editora da Unicamp, 2002.
[6] SILVA, Naiguel Alventino. OS NÚMEROS DE STIRLING. Dissertação– UFGD, 2018.(Último acesso em 01/06/20)
[7] Clubes de Matemática da OBMEP: Fatorial e Permutação Simples(Último acesso em 01/06/20)
[8] MacTutor: James_Stirling (matemático)(Último acesso em 01/06/20)
[9] Números de Stirling (Último acesso em 01/06/20)
[10] Portal da Matemática:Análise Combinatória – Permutação Circular(Último acesso em 01/06/20)
[11] Portal da Matemática:Permutações circulares(Último acesso em 01/06/20)
[12] Stirling numbers and Pascal triangles | Wild Linear Algebra A 23 | NJ Wildberger(Último acesso em 01/06/20)
[13] Wikipedia: Jacobitismo(Último acesso em 01/06/20)
[14] Wikipedia: James_Stirling_(mathematician)(Último acesso em 01/06/20)
[15] Wikipedia: James_Stirling (matemático)(Último acesso em 01/06/20)
[16] Wikipedia: Permutation (Último acesso em 01/06/20)