Um pouco sobre polígonos
 |
Para estudarmos geometricamente as chamadas estrelas, precisaremos de uma definição mais geral de polígono. Vejamos.
|
Uma segunda definição de polígonos

 |
Com essa nova definição, todas as figuras que, até então, estávamos chamando de polígonos continuam sendo consideradas polígonos. Mas algumas figuras que não eram consideradas polígonos, por apresentarem lados cruzados, com essa definição serão consideradas polígonos.
|

|
Espera um pouco… |
 |
 |
Calma, não é bem assim… |

 |
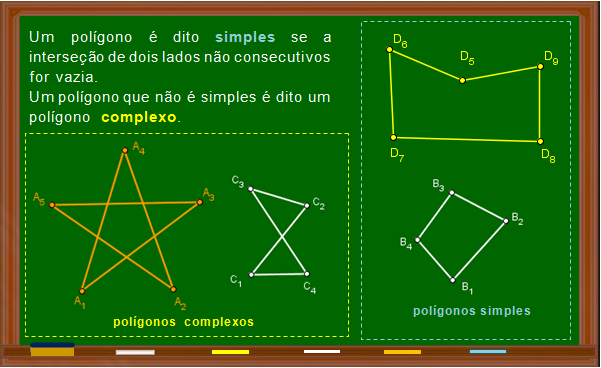
Agora que restabelecemos uma linguagem básica, vamos nos reencontrar com as figuras que foram classificadas como polígonos, segundo a nossa primeira definição. Ao compararmos as duas definições, observamos que elas diferem apenas quanto às interseções de lados não consecutivos das figuras classificadas como polígonos, por cada uma delas. Enquanto a primeira definição exige que “se lados de um polígono se intersectam, nessas interseções encontramos apenas vértices”; na segunda definição não existe essa exigência. |
 |
Continuaremos reapresentando mais algumas definições e considerações já vistas na sala Polígonos, uma primeira definição, mas não sem antes alertar que é usual se definir polígonos convexos apenas para polígonos simples. |

|
Entendi! |
|
 |
Isso mesmo, como essa segunda definição de polígono permite interseções entre lados não consecutivos, as nossas estrelas podem, agora, ser classificadas como polígonos. |
Estrelas definidas como polígonos
Neste tópico, utilizaremos a definição de polígono estabelecida nesta Sala e o que foi discutido sobre estrelas na Sala Estrelas 2. Iniciaremos a discussão deste tópico estabelecendo uma definição básica de estrela como um polígono.
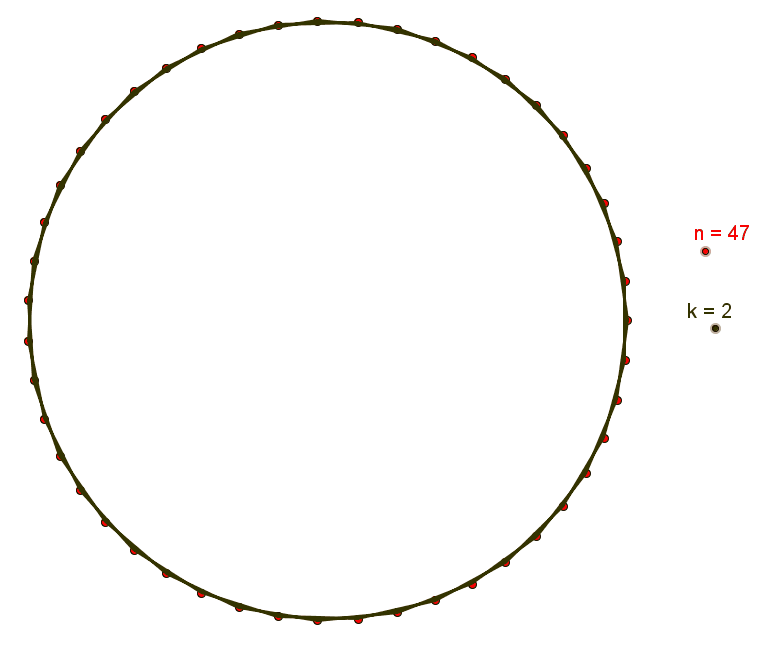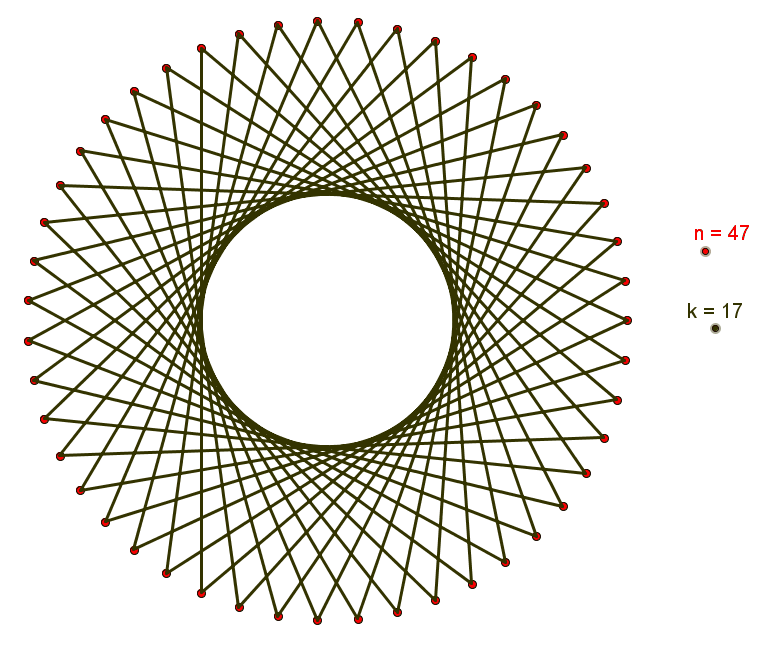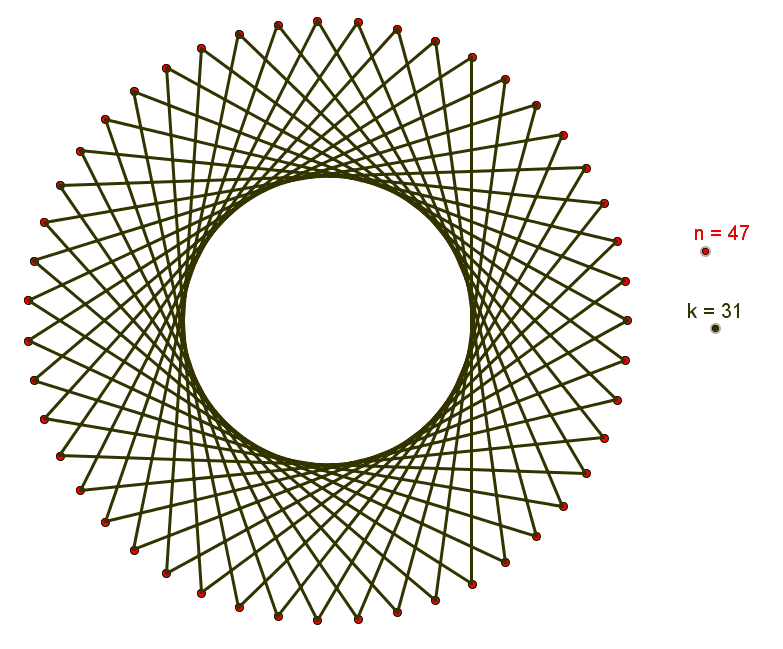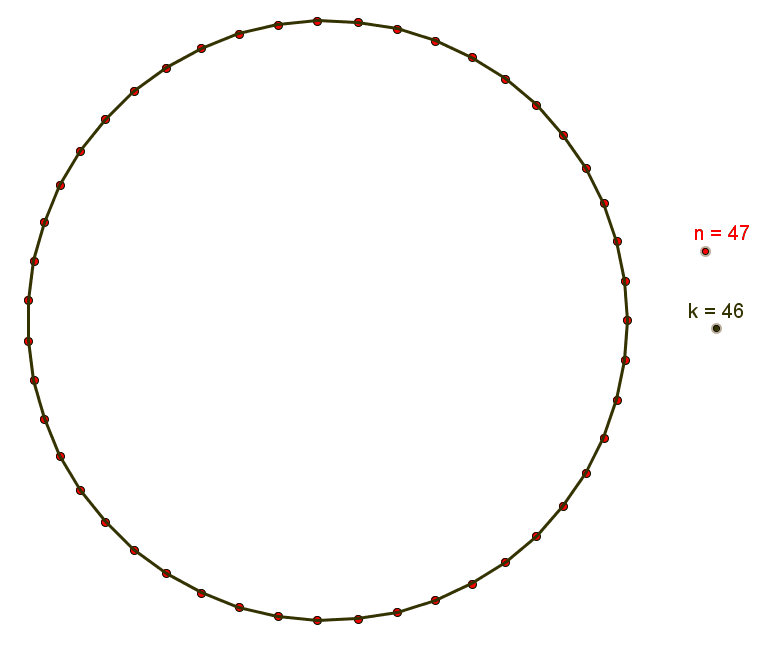
Chamamos de polígono estrelado n / k o polígono complexo de [tex]n[/tex] lados obtido a partir da divisão de uma circunferência em [tex]n[/tex] partes congruentes, ligando-se sucessivamente os pontos de divisão de [tex]k[/tex] em [tex]k[/tex].
A notação fracionária [tex] n / k[/tex] mostra a íntima relação dos polígonos estrelados com a Teoria dos Números e foi estabelecida pelo matemático suíço Ludwig Schläfli (1814 – 1895).
Fixados [tex]n[/tex] e [tex]k[/tex] nas condições da definição, observamos que o polígono estrelado n / k é uma figura (n , k) . Assim, se tomarmos [tex] 1 < k \lt \dfrac{n}{2}[/tex], o polígono estrelado n / k é o mesmo que o polígono estrelado n / (n – k) uma vez que o polígono estrelado que se obtém unindo os pontos de divisão da circunferência em um sentido e no sentido contrário é o mesmo. Dependendo do valor fixado [tex]n[/tex], podemos ter mais de um polígono estrelado de [tex]n[/tex] lados; nesses casos, basta tomarmos diferentes números naturais [tex]k[/tex] satisfazendo as condições da definição.
Feitas essas observações, vejamos alguns exemplos.
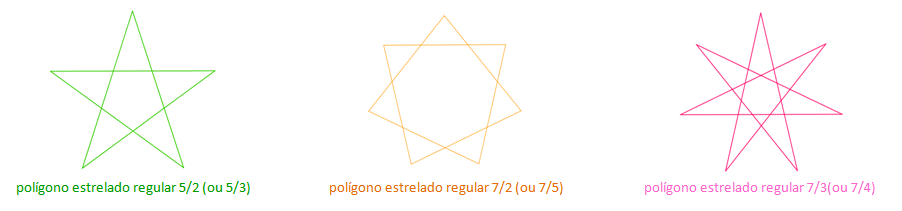
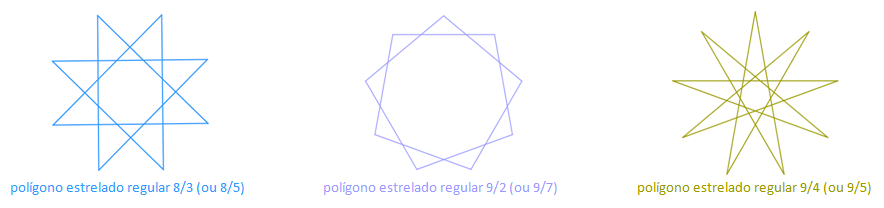
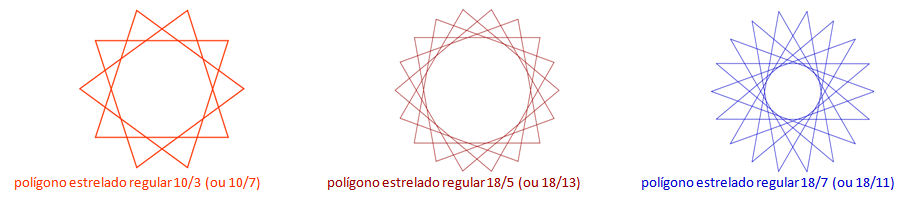

[tex] 47 / 2 \, , \, 47 / 3 \, , \, 47 / 4 \, , \, . . . \, , \, 47 / 43 \, , \, 47 / 44 \, [/tex] e [tex] \, 47 / 45[/tex] ,
num total de 22 polígonos estrelados distintos.
Fabricando estrelas
Você poderá fabricar seus próprios polígonos estrelados com até 40 vértices utilizando o applet abaixo.
Clicando no botão, o aplicativo abrirá em outra janela.
Bom divertimento!
|
Eu gostei, agora posso fazer muitas estrelas!!! |

|
 |
Esse último aplicativo foi construído a partir do roteiro que estabelecemos na Sala anterior, pois o roteiro funciona como um algoritmo. |
Passando o roteiro a limpo
Escolha um número natural [tex] n [/tex], com [tex]n \gt 1[/tex], divida uma circunferência em [tex] n [/tex] arcos congruentes e sejam [tex]A_1, \, A_2, \, \cdots , A_n [/tex] os pontos que dividem a circunferência nas [tex]n[/tex] partes iguais. Para cada inteiro [tex] k [/tex] tal que [tex] 0 < k < n [/tex], que objeto geométrico obtemos ao ligarmos consecutivamente, a partir de [tex]A_1[/tex], pontos da divisão por segmentos de reta, saltando de [tex]k[/tex] em [tex]k[/tex] pontos, até retornarmos ao ponto inicial [tex]A_1[/tex]?
O roteiro abaixo fornece a resposta dessa pergunta.
Sejam [tex] n [/tex] e [tex] k [/tex] números naturais tais que [tex] 0 \lt k \lt n [/tex].
⇝ Passo 1: Verifique se [tex]k \le \dfrac{n}{2}[/tex].
- Se [tex]k \le \dfrac{n}{2}[/tex], faça [tex]t = k[/tex] e aplique os passos seguintes.
- Se [tex]k \gt \dfrac{n}{2}[/tex], faça [tex]t = n – k [/tex] e aplique os passos seguintes.
Com esse passo asseguramos que trabalharemos apenas com números naturais não nulos, no máximo, iguais a [tex]\dfrac{n}{2}[/tex] e sem perder a generalidade do problema, uma vez que os objetos geométricos obtidos saltando-se de [tex] k [/tex] em [tex] k [/tex] pontos e de [tex]n-k [/tex] em [tex] n-k [/tex] pontos são iguais.
⇝ Passo 2: Verifique se [tex]t=\dfrac{n}{2}[/tex].
- Se [tex]t = \dfrac{n}{2}[/tex], então [tex] n [/tex] é par, o objeto geométrico obtido é um segmento de reta e a pergunta está respondida.
- Se [tex]t \ne\dfrac{n}{2}[/tex], vá para o Passo 3.
Se o próximo Passo for executado, significa que [tex]t \ne \dfrac{n}{2}[/tex].
Portanto, nos próximos passos, [tex]t \lt \dfrac{n}{2} \, [/tex] e [tex] \, n \gt 2 [/tex], necessariamente.
⇝ Passo 3: Verifique se [tex]t = 1 [/tex].
- Como [tex]n \gt 2 [/tex], se [tex]t = 1 [/tex], então o objeto geométrico obtido é um polígono regular de n lados e a pergunta está respondida.
- Se [tex]t \ne 1 [/tex], vá para o Passo 4.
Antes de executarmos o Passo 4, precisamos calcular o [tex]mdc(n , t)[/tex].
⇝ Passo 4: Seja [tex]d = mdc(n , t)[/tex].
- Se [tex]d = 1[/tex], como [tex]t \ne 1 [/tex], então o objeto geométrico obtido é um polígono estrelado de n pontas e a pergunta está respondida.
- Se [tex]d \ne 1[/tex], vá para o Passo 5.
Importante: Se o próximo passo for executado, então [tex]d = mdc(n , t) \ne 1[/tex], assim [tex]\dfrac{n}{d} \lt n \, [/tex] e [tex] \, \dfrac{n}{t} \lt n[/tex].
⇝ Passo 5: Verifique se [tex]t [/tex] é um divisor de [tex]n[/tex].
- Se [tex]t [/tex] for um divisor de [tex]n [/tex], o objeto geométrico obtido é um polígono regular de [tex]\dfrac{n}{t}[/tex] lados e a pergunta está respondida.
- Se [tex] t [/tex] não for um divisor de [tex] n [/tex], então o objeto geométrico obtido é um polígono estrelado de [tex]\dfrac{n}{d}[/tex] pontas e a pergunta está respondida.
 |
Não poderíamos encerrar nossa discussão antes de deixarmos alguns problemas para serem resolvidos, a partir da definição geral de polígonos dada nesta Sala. |
Problemas envolvendo polígonos
Problema 1:
Se [tex]d[/tex] é o número de diagonais de um polígono, convexo ou não, de [tex]n[/tex] lados, [tex]n \ge 3[/tex], mostre que [tex]d=\dfrac{n (n-3)}{2}[/tex].
Problema 2:
Seja [tex]S_i[/tex] a soma das medidas, em graus, dos ângulos internos de um polígono convexo de [tex]n[/tex] lados, [tex]n \ge 3[/tex]. Mostre que [tex]S_i=(n-2) \cdot 180^{\circ}[/tex].
Problema 3:
Ângulo externo de um polígono convexo é um ângulo suplementar adjacente a um ângulo interno do polígono em questão.
Mostre que a soma das medidas, em graus, dos ângulos externos de um polígono convexo de [tex]n[/tex] lados, [tex]n \ge 3[/tex], tomados um por vértice, é sempre [tex]360^{\circ}[/tex].
Problema 4:
O número de diagonais a partir de um dos vértices de um polígono regular é igual ao número de diagonais de um hexágono. Determine:
(a) O número de lados desse polígono.
(b) O total de diagonais desse polígono.
(c) A soma das medidas dos ângulos internos desse polígono.
(d) A soma das medidas dos ângulos externos desse polígono.
Problema 5:
Sejam [tex]a, \, b, \, c, \, d, \, e, \, f[/tex] as medidas, em graus, dos ângulos indicados na figura abaixo.
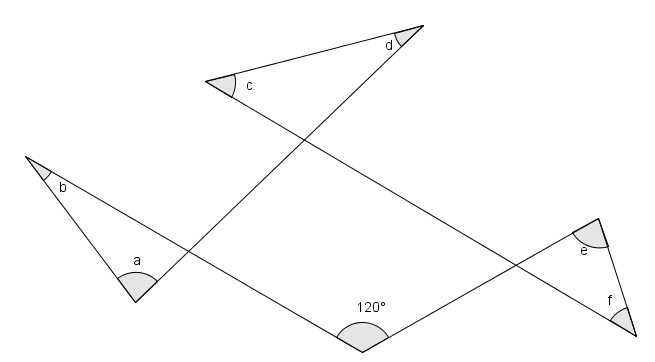
Determine [tex]a+b+c+d+e+f[/tex].
Problema 6:
Determine a medida, em graus, do ângulo formado pelos prolongamentos dos lados [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex] de um polígono regular de [tex]30[/tex] lados.
A medida de cada ângulo externo de um polígono regular é [tex]\dfrac{1}{4}[/tex] da medida de cada um de seus ângulos internos. Que polígono é esse?
Qual é a medida de um ângulo interno de um polígono regular que tenha 35 diagonais?
Problema 9:
A partir de uma estrela falsa de 6 pontas, foi construído o polígono não convexo de 12 lados [tex]ABCDEFGHIJKL[/tex] mostrado na figura.
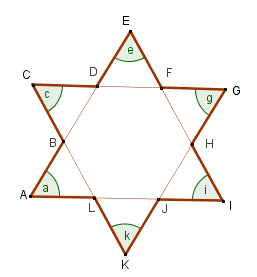
Determine as medidas dos ângulos assinalados.
O polígono não convexo de 16 lados mostrado na figura abaixo foi construído a partir de uma estrela falsa de 8 pontas.
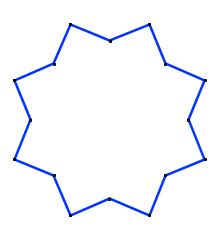
Determine as medidas dos ângulos agudos definidos pelas pontas desse polígono.
Problema 11:
Quantos polígonos estrelados regulares distintos podem ser traçados a partir de uma circunferência que foi dividida em 26 partes iguais?
E em 45 partes iguais?
E em [tex]n[/tex] partes iguais, com [tex]n\gt4[/tex]?
Problema 12:
O quadrilátero [tex]ABCD[/tex], indicado na figura abaixo, foi obtido a partir de um pentágono regular e de um polígono estrelado regular de cinco lados.
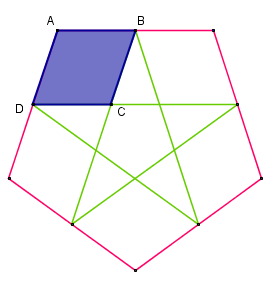
Que tipo de quadrilátero é [tex]ABCD[/tex]?
Determine os ângulos internos de [tex]ABCD[/tex].
No applet abaixo, foi fixada uma circunferência dividida em 14 partes iguais. Assim, aproveite o aparato e, utilizando os pontos da divisão, construa:
(a) um polígono regular com 14 lados;
(b) um segmento de reta;
(c) um polígono estrelado com 14 lados;
(d) um polígono regular com menos de 14 lados;
(e) um polígono estrelado com menos de 14 lados.
Antes de utilizar o applet, leia as instruções.
Equipe COM – OBMEP